图论基础
树和图的存储
无向图:没方向
建图需要在两个节点间建两条相反的边
add(a, b), add(b, a);
有向图:有方向
领接矩阵:g[a,b] = 权重$a\to b$
邻接表(常用):每个点上都有一个单链表,存储该点能到哪些点上去
若有权重则加个w[N]数组,以idx为下标记录权值
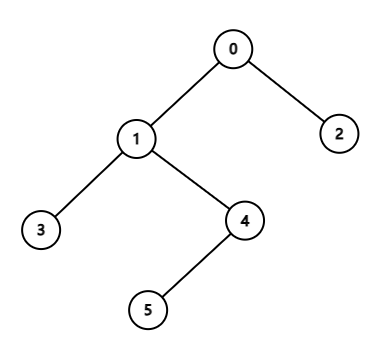
| 1 | 2,3 |
|---|---|
| 2 | 4,5 |
| 3 | NULL |
| 4 | NULL |
| 5 | 6 |
| 6 | NULL |
模板:
int h[N], e[M], ne[M], idx;
// 头节点 节点的值 节点的边
// 插入
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// 初始化
memset(h, -1, sizeof(h));
一般稠密图使用邻接表,稀疏图使用邻接矩阵
稠密图是指边数接近于最大边数的图:$\frac{n(n-1)}{2}$
稀疏图是一种边数接近于最小边数的图:$n-1$
树就是无环连通图
树和图的遍历
深度优先搜索
// 再开一个bool数组来存储那些点被搜索过了
bool st[N];
void dfs(int u) {
st[u] = true; // 标记被搜索过的
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (!st[j]) dfs(j);
}
}
dfs(1);
宽度优先遍历
int d[N], q[N];
// 距离 队列
int bfs() {
int hh = 0, tt = 0;
q[0] = 1;
memset(d, -1, sizeof (d));
d[1] = 0;
while (hh <= tt) {
int t = q[hh++];
for (int i = h[t]; i != -1; i = ne[i]) { // 拓展
int j = e[i];
if (d[j] == -1) {
d[j] = d[t] + 1;
q[++tt] = j;
}
}
}
return d[n];
}
拓扑序列
一般用来求图的拓扑序列
有向图才有拓扑序列,若一个图中所有点构成的序列A满足对于图中的每一条边$x\to y$,都有x出现在y前面,所以不能出现环
将入度为0的点入队,扩展后将入读为0的点与后面的点的连接删除,宽度搜索
至于环不存在入读为0的点
int d[N], q[N];
// 节点入读 队列
bool topsort() {
int hh = 0, tt = 0;
for (int i = 1; i <= n; i++) {
if (!d[i]) { // 将所有入度为0的节点入队
q[++tt] = i;
}
}
while (hh <= tt) {
int t = q[hh++];
for (int i = h[t]; i != -1; i = ne[i]) { // 扩展
int j = e[i];
d[j]--; // 删除前面节点与当前节点的连接(效果就是入度减小)
if (!d[j]) q[++tt] = j; // 若为0了则入队
}
}
return tt == n;
}
add(a, b);
d[b]++; // 记录节点入读
for (int i = 1; i <= n; i++) cout << q[i] << ' '; // 如果存在则队列q中就是拓扑序列
最短路
令n为点的数量,m为边的数量
问题:
- 单元最短路:从一个点到其他所有点的最短路问题(以下模板都从1开始)
- 所有边的权重都是正数
- 朴素Dijkstra算法$O(n^2)$——稠密图(邻接矩阵)
- 堆优化版的Dijkstra算法$O(m\log{n})$——稀疏图(邻接表)
- 存在负权边
- Bellman-Ford $O(nm)$
- SPFA 一般$O(m)$,最坏$O(nm)$
- 所有边的权重都是正数
- 多源汇最短路:任选两个点,从一个点走到另一个点的最短路问题
- Floyd算法$O(n^3)$
单元最短路
朴素Dijkstra算法
$O(n^2)$
- 先初始化距离:$ dist[1] = 0,\ dist[other] = +\infty$$
- 迭代更新
- 循环:$0\to n$,找到不在S中的距离最近的点t
- 将t放到集合S里(S:当前已经确定的最短距离的点)
- 用t更新其他点的距离(判断$1\to x的距离是否大于1\to t\to x的距离$:
dist[x] > dist[t] + w如果成立就把距离更新)
稠密图,还要带上权重,我们使用邻接矩阵
int n, m;
int g[N][N], dist[N]; // 邻接矩阵 距离
bool st[N]; // S集合
int dijkstra() {
memset(dist, 0x3f, sizeof(dist));
dist[1] = 0;
for (int i = 0; i < n; i++) {
int t = -1;
for (int j = 1; j <= n; j++)
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
st[t] = true;
for (int j = 1; j <= n; j++) {
dist[j] = min(dist[j], dist[t] + g[t][j]); // 用1到t的距离来更新1到j的距离
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
else return dist[n];
}
// 若存在重边和自环可以在初始化g数组时过滤
g[a][b] = min(g[a][b], c);
堆优化版的Dijkstra算法
优化思路
首先将 优先队列 定义成 小根堆,将源点的距离初始化为 0 加入到优先队列中,然后从这个点开始扩展。先将队列中的队头元素 ver 保存到一个临时变量中,并将队头元素出队,然后遍历这个点的所有出边所到达的点 j,更新所有到达的点距离源点最近的距离。
如果源点到j点的距离比源点先到 ver 点再从 ver 点到 j 点的距离大,那么就更新 dist[j],使 dist[j] 到源点的距离最短,并将该点到源点的距离以及该点的编号作为一个 pair 加入到优先队列中,然后将其标记,表示该点已经确定最短距离。因为是小根堆,所以会根据距离进行排序,距离最短的点总是位于队头。一直扩展下去,直到队列为空。
因为有 重边 的缘故,所以该点可能会有冗余数据,即如果在扩展的时候,第一次遍历到的点是 2 号点,距离 源点 的距离为 10,此时 dist[2] = 0x3f3f3f3f > dist[1] + distance[1 -> 2] = 0 + 10 = 10 所以 dist[2] 会被更新为 10,此时会将 {10, 2} 入队。但是很不巧从 源点 到 2 号点有一个距离为 6 的重边,当遍历到这个重边时,由于 dist[2] = 10 > dist[1] + distance[1 -> 2] = 0 + 6 = 6,所以 {6, 2} 也入队了,入队之后由于是 小根堆 所以 {6, 2} 会排在 {10, 2} 前面,所以 {6, 2} 会先出队,出队之后会被标记。所以当下一次再遇到已经被标记的 2 号点时,直接 continue 忽略掉冗余数据继续扩展下一个点即可。
稀疏图,使用邻接表,这样也就不需要考虑重边的问题,算法本身已经处理了
typedef pair<int, int> PII; // 距离 编号
// 在pair中排序优先看前面的元素
int n, m;
int w[N], h[N], e[N], ne[N], idx; // w[]权重
int dist[N];
bool st[N];
int dijkstra() {
memset(dist, 0x3f, sizeof(dist));
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap; // 默认大根堆,修改成小根堆
heap.push({0, 1});
while (heap.size()) {
auto t = heap.top();
heap.pop();
int ver = t.second, distance = t.first;
if(st[ver]) continue;
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] > distance + w[i]) {
dist[j] = distance + w[i];
heap.push({dist[j], j});
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
else return dist[n];
}
最和dist[]中存着的就是从源点到各点的最短距离
Bellman-Ford算法
求带负权值的最短路
一般用SPFA来做,但要是存在负权回路的话就只能使用Bellman-Ford,因为其循环的次数是有限制的因此最终不会发生死循环
Bellman-Ford对边的存储没有要求,只需要能遍历到所有边就行,所以可以使用结构体
struct {
int a, b, w;
} ed[N]; // 边的个数
步骤:
- 迭代n次,每次循环所有边$a\stackrel{w}{\longrightarrow}b$
- 在每次循环中更新所有边
dist[b] = min(dist[b], dist[a] + w)(松弛操作)
在完成上述循环后一定存在三角不等式:$dise[b] \leq dist[a] + w$
若存在负权回路则会一直循环,可能求不出最短路(即为负无穷),直到消耗完次数
struct Edge
{
int a, b, w; // 出点 入点 权重
}edges[M];
int bellman_ford() {
memset(dist, 0x3f, sizeof(dist));
dist[1] = 0;
// 如果第n次迭代仍然会松弛三角不等式,就说明存在一条长度是n+1的最短路径,由抽屉原理,路径中至少存在两个相同的点,说明图中存在负权回路
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
int a = edges[j].a, b = edges[j].b, w = edges[j].w;
dist[b] = min(dist[b], dist[a] + w);
}
}
// 可能会存在两个无穷大的点间是负权但也更新的情况:
// 无穷--(-3)-->无穷 更新:无穷--(-3)-->无穷-3,就比无穷要小了
if (dist[n] > 0x3f3f3f3f / 2) return -1;
return dist[n];
}
若对边的个数有限制的话添加backup[]修改for判断即可:
for (int i = 0; i < k; i++) {
memcpy(backup, dist, sizeof(dist));
for (int j = 0; j < m; j++) {
int a = edges[j].a, b = edges[j].b, w = edges[j].w;
dist[b] = min(dist[b], backup[a] + w);
}
}
SPFA算法
已死
本质是使用优先队列优化Bellman-Ford算法
有负权回路的话不能使用,因为用了队列来存储,只要发生了更新就会不断的入队,所以用SPFA会死循环
原理:
在dist[b] = min(dist[b], dist[a] + w);中只有dist[a]变小了dist[b]才会变小,所以将所有变小了的节点存入队列,再用队列里的节点更新即可(只有我变小了,我后面的人才会变小)
步骤:
- 先将起点放入队列
queue <- 1 - 只要队列不空就一直循环
while (queue不空)- 取出对头
t -> q.front q.pop - 更新
t的所有出边t --(w)--> b - 更新成功先判断队列里有没有
b,没有就将b插入队列,有就跳过
- 取出对头
// 与Dijkstra算法很像
int spfa() {
memset(dist, 0x3f, sizeof(dist));
dist[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;
while (q.size()) {
int t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] > dist[t] + w[i]) {
dist[j] = dist[t] + w[i];
if (!st[j]) {
q.push(j);
st[j] = true;
}
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
当然也可以用此来求是否有负权回路:
使用一个数组cnt[x]存储边数,根据抽屉原理若cnt[x] >= n则其中一定至少存在两个点的值是相同的,即存在负环
这里不需要初始化,主要是要看一个相对变小的状态,所以没必要初始化以求最短路精确值,重点是看到dist减小的趋势,所以与dist全零或是全无穷无关
dist[x] = dist[t] + w[i];
cnt[x] = cnt[t] + 1;
bool spfa() {
queue<int> q;
for (int i = 1; i <= n; i++) {
st[i] = true;
q.push(i);
}
while (q.size()) {
int t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] > dist[t] + w[i]) {
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1;
if (cnt[j] >= n) return true;
if (!st[j]) {
q.push(j);
st[j] = true;
}
}
}
}
return false;
}
多源汇最短路
Floyd算法
使用动态规划,核心:d[i][j] = min(d[i][j], d[i][k] + d[k][j])
以每个点为中转站,刷新所有入度和出度的距离
使用邻接矩阵
void floyd() {
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
// 初始化
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (i == j) d[i][j] = 0; // 到自己距离为0,到其他点距离为INF
else d[i][j] = INF;
}
}
最小生成树
最小生成树是最小权重生成树的简称
定义:在$n$个节点的无向图中通过$n-1$条边构成边权和最小的树
- 普利姆算法(Prim)
- 朴素版Prim$O(n^2)$——稠密图
- 堆优化版Prim$O(m\log{n})$——稀疏图(不常用)
- 克鲁斯卡尔算法(Kruskal)$O(m\log{m})$——稀疏图
普利姆算法
朴素版Prim
与Dijkstra算法很像,基于贪心
-
先将所有距离初始化为无穷
dist[i] = INF -
n次迭代
- 找到集合外距离最近的点,赋值给t
- 用t更新其他点到集合的距离(Dijkstra是更新其他点到起点的距离)
- 把t加到集合中
st[t] = true
搞不懂可以看这篇blog最小生成树——Prim算法,注意dist数组的变化
int prim() {
memset(dist, 0x3f, sizeof(dist));
int res = 0;
for (int i = 0; i < n; i++) {
int t = -1;
for (int j = 1; j <= n; j++) {
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
}
if (i && dist[t] == INF) return INF;
if(i) res += dist[t];
for (int j = 1; j <= n; j++) dist[j] = min(dist[j], g[t][j]);
st[t] = true;
}
return res;
}
堆优化版Prim
(不常用,之后再补)
克鲁斯卡尔算法(Kruskal)
基于贪心和并查集
- 将所有边按权重从小到大排序()
- 枚举每条边$a\to b$,权重$c$
- 如果$a\to b$不连通,则将这条边加到集合中去
struct Edge {
int a, b, w;
bool operator< (const Edge &W)const {
return w < W.w;
}
}edges[N];
sort(edges, edges + m);
for (int i = 1; i <= n; i++) p[i] = i; // 初始化并查集
int res = 0, cnt = 0; // 最小生成树的边的权重之和 当前加入多少条边
for (int i = 0; i < m; i++) {
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
a = find(a), b = find(b);
if (a != b) {
res += w;
cnt++;
p[a] = b;
}
}
// cnt < n - 1则不连通
二分图
一个图是二分图当且仅当图中不含奇数环(长度为奇数的环)(充要条件)
- 染色法$O(n+m)$
即尝试用两种颜色标记图中的节点,当一个点被标记后,所有与它相邻的节点应该标记与它相反的颜色,若标记过程产生冲突,则说明一条边两边染色相同,一定存在奇环。可以用DFS来实现。
使用邻接矩阵
bool dfs(int u, int c) {
color[u] = c;
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (!color[j]) { // 如果还没有被染色
if (!dfs(j, 3 - c)) return false;
}
else if (color[j] == c) return false; // 一条边两边染色相同,一定存在奇环
}
return true;
}
bool flag = true;
for (int i = 1; i <= n; i++) {
if (!color[i]) {
if (!dfs(i, 1)) { // 定义染色出现问题就返回false
flag = false;;
break;
}
}
}
- 匈牙利算法$O(mn)$,实际运行时间一般远小于$O(mn)$
匈牙利算法主要用于解决一些与二分图匹配有关的问题
二分图的最大匹配
在二分图的子图中任意两边都没有公共节点则为一个匹配,含边数最多的一组匹配称为二分图的最大匹配
设左边节点为男生,右边节点为女生,男女相亲,男选女,可占可让,贪心配对
根据算法原理在存储图的时候只需要让左边指向右边即可
使用邻接表
流程:
- 枚举n个男生
- 每轮
st[]初始化为0(即女生皆可选) - 每轮若能配对
res + 1
- 每轮
- 枚举男生
u配对的女生v- 若女生已标记,则跳过
- 若女生没标记,则配对
- 若女生配对的男生可让出,则配对
- 否者枚举
u的下一个v
- 若枚举完
u对应的v都不能匹配,则返回false
关于st[]:
首先 find(x) 遍历属于h[x]的单链表相当于遍历他所有喜欢的女生
而如果女j之前就被男k匹配过了,那我们就find(k),然后在find(k)的过程中,因为st[j]=true,这时候男k就不能再选则女j了,因为女j已经被预定了,所以男k就只能在他喜欢的女生里面选择其他人来匹配
这也说明了枚举每个男生时都需要将st[]重置的原因
int match[N]; // 存女生v的男友
bool st[N]; // 存女生v是否被访问
bool find(int x) {
for (int i = h[x]; i != -1; i = ne[i]) {
int j = e[i];
if (!st[j]) {
st[j] = true;
if (match[j] == 0 || find(match[j])) { // 没被匹配或能为匹配她的男生找到另外一个女生
match[j] = x;
return true;
}
}
}
return false;
}
int res = 0;
for (int i = 1; i <= n1; i++) {
memset(st, false, sizeof(st)); // 重置st
if (find(i)) res++;
}
cout << res << endl;