我认为理解回文自动机需要图,以\(abbaabba\)为例,它的回文树是这样的:
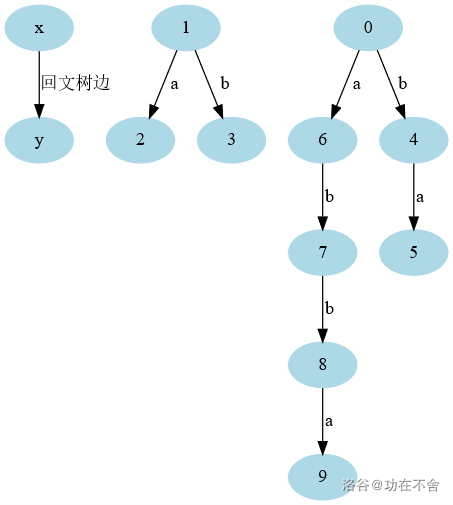
令树上的每一个点为一个回文串,其中,\(1\)为根的树中的点回文串长度为奇数,且最中间的那个字母就是\(1\)连向其他点的的边的字母,而\(0\)为根的树中的点回文串长度为偶数。
举点例子吧:点\(2\)的回文串为\(a\),点\(3\)的回文串为\(b\),点\(4\)的回文串为\(bb\),点\(5\)的回文串为\(abba\),点\(8\)的回文串为\(bbaabb\)
规律很明显,但我不会表达(逃),简单来说,感性理解,就是深度越小的边,它代表的字母位置在越里面。
考虑构造出这种回文树
引入\(fail\)数组:
再来一张图:
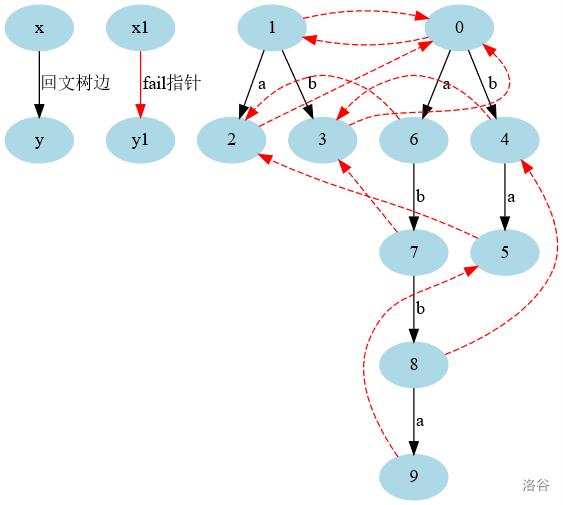
其中,\(fail\)数组指向的是该回文串中的最长回文后缀
很好理解,自己看
对于\(abb\)来说,若新插入了\(a\),如何更新回文树?
第一步:找到\(abb\)的最长回文后缀,即\(bb\),这个已经找到了,是上次更新回文树的时候
第二步:找到\(bb\)的前一个字母,即\(a\),与插入的字母,即\(a\)比较,若相同,则在表示回文\(bb\)的点后面连一条\(a\)的边,表示\(abba\),然后去更新\(fail\)数组,若不相同,则寻找\(bb\)的最长回文后缀,重复上述操作,知道可以或已经没有最长回文后缀为止。
考虑更新\(fail\)数组,这个与上述步骤相似,不同的只有要从\(bb\)的最长回文后缀开始找,即\(b\),理由是防止最长回文后缀是自己,而且是最长回文后缀
时间复杂度,对于一个新插入的字母,我们最多新增一个节点,总共最多有\(n\)个节点,而我们在枚举上述步骤时失配只会往前跳,所以总共条\(n\)次,所以时间复杂度是\(O(n)\)
上代码:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll N=2e6+50;
char s[N];
ll n,len[N],fail[N],last,tot=1,cur,trie[N][26],pos,num[N];
ll getfail(ll x,ll i)
{
while(i-len[x]-1<0||s[i-len[x]-1]!=s[i]) x=fail[x];
return x;
}
int main()
{
scanf("%s",s);
n=strlen(s);
fail[0]=1,len[1]=-1;
for(ll i=0;i<n;i++)
{
if(i!=0) s[i]=(s[i]+last-97)%26+97;
pos=getfail(cur,i);
if(!trie[pos][s[i]-'a'])
{
fail[++tot]=trie[getfail(fail[pos],i)][s[i]-'a'];
trie[pos][s[i]-'a']=tot;
len[tot]=len[pos]+2;
num[tot]=num[fail[tot]]+1;
}
cur=trie[pos][s[i]-'a'];
last=num[cur];
printf("%lld ",last);
}
return 0;
}