Summer Pokemon

想认识一下这位朋友QWQ

Solution

以下规定：\(n, m\) 为原题中 \(n, m\)，\(x\) 表示一次对决的判定轮数。

\(a, b\) 为长度为 \(x\) 的 单增数组（具体意义见下），\(|a\cup b| = 2x, a \cup b = \{1, 2, \dots, 2x \}\)。

算法一

我会爆搜！

测试点 \(2\) 启发你，你只需要求出安排双方出战岛可梦的 排名 的方案数，最后再将结果乘上 \(\binom{m}{2x}\) 即可。

期望得分 \(10pts\)。

算法二

我会卡特兰数！

性质 \(A\) 启发你，可以先把该问题放到序列上进行分析。

性质 \(B\) 启发你，可以先考虑一次对决中所有判定结果均相同的情况。

由于我们只关心排名，我们记 \(a\) 表示嗨梨方岛可梦的排名情况，\(b\) 表示 umi 方岛可梦的排名情况。

根据对决的方式，将 \(a, b\) 排序以后，同一下标双方的排名大小决定了该轮判定的胜负情况。

当判定结果全部相等时，排名分配数等价于 \(x\) 对括号的合法括号序列数，即卡特兰数 \(f_x = \frac{\binom{2x}{x}}{x + 1}\)。

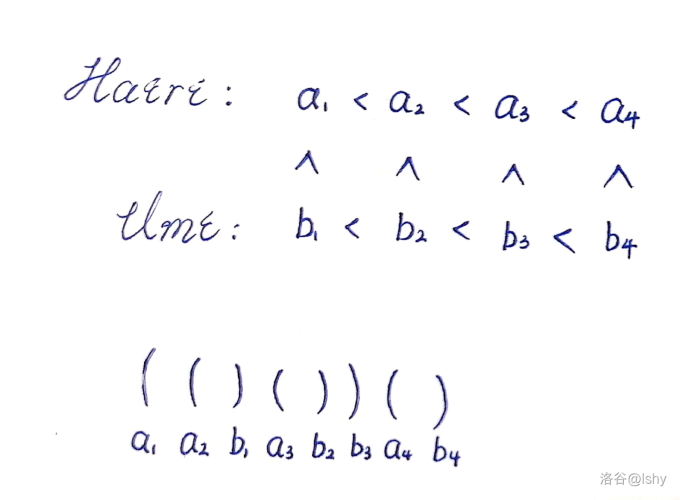
结合算法一，期望得分 \(40pts\)。

算法三

我会找性质！

我们已经会了一段判定结果相等（即胜负序列为全 \(0/1\)）时的做法，是否能把普通的 \(01\) 序列分成若干段连续全 \(0/1\) 序列考虑，再把结果拼起来？

你发现一段连续的全 \(0/1\) 区间对应的 \(a, b\) 的值域是连续的！那么每一段值域也就成了确定的！所以普通 \(01\) 序列的方案数就是每一段连续 \(0/1\) 序列对应的方案数的乘积。

结合算法一、二，期望得分 \(70pts\)。

算法四

我会倍增！

维护每个点 \(i\) 到根节点对应 \(01\) 序列的方案数 \(w_i\)，这是容易的。

如果要查询点对 \((u, v)\)，情况如下图所示：（用实心表示 \(1\)，空白代表 \(0\)）

（\(u^{'}\) 表示在 \(u - lca\) 链上、并与 \(lca\) 处于同一连通块内的距 \(lca\) 最远点，\(v^{'}\) 表示在 \(v - lca\) 链上、并与 \(lca\) 处于同一连通块内的距 \(lca\) 最远点。图片中没解释清楚，请以上述进行理解）

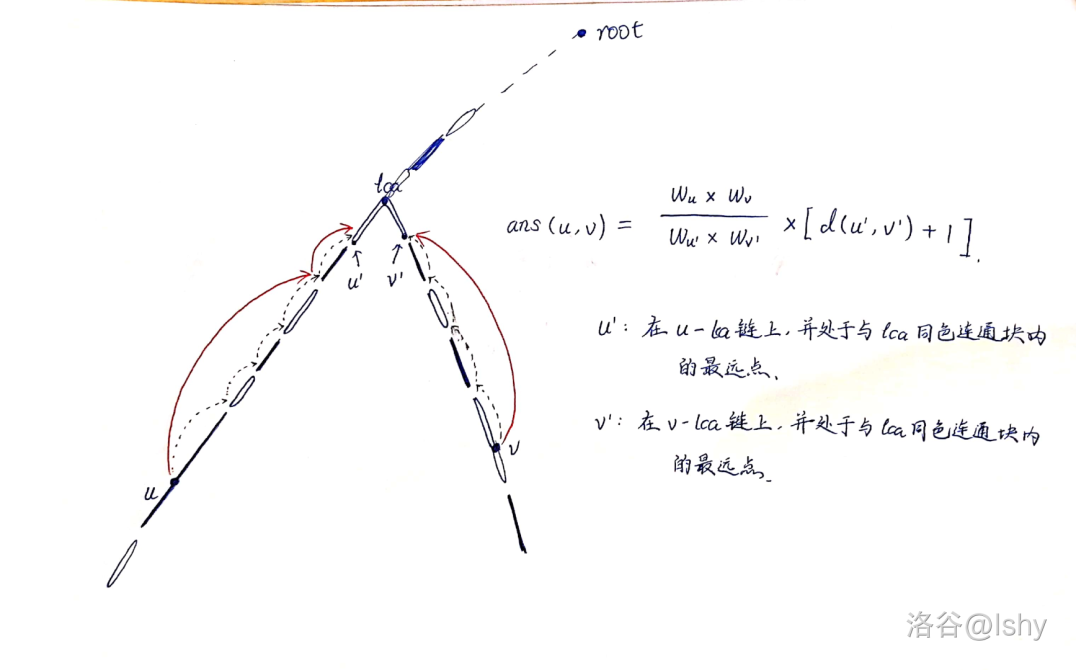
现在只需快速求出 \(u^{'}, v^{'}\) 即可。

如果我们暴力找，思路是向上跳到与当前点不同色的最低点，使得跳上去后不会越过 \(lca\)，如图中虚线所示。

那么我们用倍增优化这个跳链过程即可，即记 \(g_{i, j}\) 表示点 \(i\) 颜色交替地向上跳跳到的第 \(2^j\) 个点，如图中红色线段所示。

期望得分 \(100pts\)。

以上所有所求的量处理方式都非常简单，除去组合数和 LCA 的板子，代码的主要部分不会超过 \(1k\)（如果你实现地好的话）。

本题放在 T3 算是一道小清新啦。姆Q？