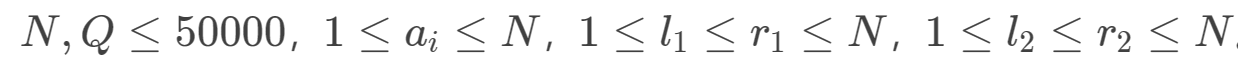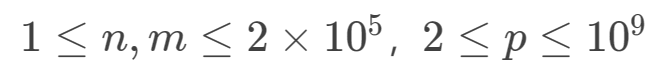首页 > 其他分享 >莫队-题1

莫队-题1

时间：2023-08-26 13:01:38浏览次数：43  
标签：suf idx int ++ while qry 莫队

XOR and Favorite Number

image-20230825223422628

题解

  • 我们考虑将问题进行转化
  • 对于一个区间\([l,r]\)中有多少个子区间异或值为\(k\)这个问题，我们考虑到异或的前缀性质，对其进行差分
  • 即：令\(pre_i\)为\([1,i]\)的前缀异或和，对于\(i,j \in [l,r],i\leq j\)，且\(pre_{i - 1} \oplus pre_j=k\)
  • 那么问题转化为：区间\([l,r]\)中有多少个二元组\((i,j)\)，满足\(pre_{i - 1} \oplus pre_j=k\)
  • 而莫队恰好适用于解决区间二元组的问题，令\(cnt[x]\)代表\(x\)的出现次数
  • 我们考虑\(add\)操作：先查询\(ans +=cnt[pre_i \oplus k]\)，再修改\(cnt[pre_i]++\)
  • \(delete\)操作是一样的
  • 小\(trick\)：将询问的\(l\)提前\(-1\)，即\(l:=l-1\)
  • 注意开$long \ long $
const int N = 1e5 + 10, M = 1e7 + 10;
const int B = sqrt(N) + 1;

int n, q, k;
int a[N], pre[N];
int cnt[M], id[N], ans[N], preAns;

struct QUERY
{
    int l, r, idx;
    bool operator<(const QUERY &t) const
    {
        if (id[l] == id[t.l])
        {
            if (id[l] & 1)
                return r < t.r;
            else
                return r > t.r;
        }
        else
            return l < t.l;
    }
} qry[N];

void build()
{
    for (int i = 1; i <= n; ++i)
        id[i] = i / B + 1;
}

void del(int i)
{
    cnt[pre[i]]--;
    preAns -= cnt[pre[i] ^ k];
}

void add(int i)
{
    preAns += cnt[pre[i] ^ k];
    cnt[pre[i]]++;
}

void solve()
{
    cin >> n >> q >> k;
    for (int i = 1; i <= n; ++i)
        cin >> a[i];
    for (int i = 1; i <= n; ++i)
        pre[i] = pre[i - 1] ^ a[i];
    build();
    for (int i = 1; i <= q; ++i)
    {
        int l, r;
        cin >> l >> r;
        l--;
        qry[i] = {l, r, i};
    }
    sort(qry + 1, qry + q + 1);
    for (int i = 1, l = 1, r = 0; i <= q; ++i)
    {
        while (l > qry[i].l)
            add(--l);
        while (r < qry[i].r)
            add(++r);
        while (l < qry[i].l)
            del(l++);
        while (r > qry[i].r)
            del(r--);
        ans[qry[i].idx] = preAns;
    }
    for (int i = 1; i <= q; ++i)
        cout << ans[i] << endl;
}

P5268 [SNOI2017] 一个简单的询问

image-20230825235417087

image-20230825235427890

题解：双前缀莫队

  • 我们将题目转化成区间二元组的形式：

从\([l_1, r_1]\)中选一个\(i\)，从\([l_2,r_2]\)中选一个\(j\)，询问有多少个二元组\((i,j)\)满足\(a_i = a_j\)

  • 但是这个是从两个区间中分别选，怎样简化呢？

  • 我们考虑差分

令\(f(l_1, r_1,l_2,r_2)\)为从\([l_1, r_1]\)中选一个\(i\)，从\([l_2,r_2]\)中选一个\(j\)，且\(a_i=a_j\)的方案数

则\(\sum get(l_1,r_1,x)\times get(l_2,r_2,x) = f(l_1, r_1,l_2,r_2)\)

假设我们从\([l_2,r_2]\)中选择了一个\(j\)，那么方案数可以差分成：从\([1,r_1]\)中选择一个\(i\)，使得\(a_i=a_j\)的方案数 减去 从\([1,l_1 - 1]\)中选择一个\(i\)，使得\(a_i=a_j\)的方案数，即

\[ f(l_1, r_1,l_2,r_2) = f(1,r_1,l_2,r_2) - f(1,l_1-1,l_2,r_2) \]

那么，同理，我们也可以从\([l_1,r_1]\)中选一个\(i\)，对区间\([l_2,r_2]\)进行差分，得到：

\[ f(l_1, r_1,l_2,r_2) \\ =f(1,r_1,l_2,r_2) - f(1,l_1-1,l_2,r_2)\\ =f(1,r_1,1,r_2) - f(1,r_1,1,l_2-1)-f(1,l_1-1,1,r_2)+f(1,l_1-1,1,l_2-1) \]

那么我们就将一个询问转化为了\(4\)个询问，只不过莫队维护的是双前缀的答案

  • 我们令\(cnt1[x]\)为前缀\([1,l]\)中\(x\)出现的次数，\(cnt2[x]\)为前缀\([1,r]\)中\(x\)出现的个数

  • 比如说我们在\([1,l]\)进行\(add\)操作变为\([1,l+1]\)时，设\(a[l+1]=x\)对答案的维护应该为：

\[ ans += cnt2[x]\\ cnt1[x]++ \]

  • 同时，因为维护的是前缀，所以我们需要调整一下莫队修改的方式
const int N = 5e4 + 10, M = 1e7 + 10;
const int B = sqrt(N) + 1;

int n, q, a[N];
int cnt1[N], cnt2[N], id[N], ans[N][4], preAns;

struct QUERY
{
    int l, r, idx1, idx2;
    bool operator<(const QUERY &t) const
    {
        if (id[l] == id[t.l])
        {
            if (id[l] & 1)
                return r < t.r;
            else
                return r > t.r;
        }
        else
            return l < t.l;
    }
} qry[N << 2];

void build()
{
    for (int i = 1; i <= n; ++i)
        id[i] = i / B + 1;
}

void del(int x, int type)
{
    if (type == 1)
    {
        cnt1[x]--;
        preAns -= cnt2[x];
    }
    else
    {
        cnt2[x]--;
        preAns -= cnt1[x];
    }
}

void add(int x, int type)
{
    if (type == 1)
    {
        preAns += cnt2[x];
        cnt1[x]++;
    }
    else
    {
        preAns += cnt1[x];
        cnt2[x]++;
    }
}

void solve()
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
        cin >> a[i];
    build();
    cin >> q;
    int idx = 0;
    for (int i = 1; i <= q; ++i)
    {
        int l1, r1, l2, r2;
        cin >> l1 >> r1 >> l2 >> r2;
        // 一个询问转化为4个询问
        qry[++idx] = {r1, r2, i, 0};
        qry[++idx] = {r1, l2 - 1, i, 1};
        qry[++idx] = {l1 - 1, r2, i, 2};
        qry[++idx] = {l1 - 1, l2 - 1, i, 3};
    }
    sort(qry + 1, qry + idx + 1);
    for (int i = 1, l = 0, r = 0; i <= idx; ++i)
    {
        if (qry[i].l > qry[i].r)
            swap(qry[i].l, qry[i].r);
        // 调整莫队的顺序
        while (r < qry[i].r)
            add(a[++r], 2);
        while (l < qry[i].l)
            add(a[++l], 1);
        while (l > qry[i].l)
            del(a[l--], 1);
        while (r > qry[i].r)
            del(a[r--], 2);
        ans[qry[i].idx1][qry[i].idx2] = preAns;
    }
    for (int i = 1; i <= q; ++i)
        cout << ans[i][0] - ans[i][1] - ans[i][2] + ans[i][3] << endl;
}

P3245 [HNOI2016] 大数

image-20230826123012576

image-20230826124203617

题解：后缀差分

  • 该题显然是询问区间中子区间个数的问题，将其转换为区间二元组问题

  • 考虑后缀差分，令\(suf[i]\)为\([i,n]\)数字串所形成的数字

那么\([l,r]\)数字串为\(\frac{suf[l] - suf[r + 1]}{10^{n - r}}\)

如果\([l,r]\)的数字串为\(p\)的倍数，则

\[\frac{suf[l] - suf[r + 1]}{10^{n - r}} \% p = 0\\ \]

当\(p \neq 2 \ and \ 5\)时，\(10^{n - r}\)与\(p\)互质，所以:

\[(suf[l] - suf[r + 1]) \% p = 0 \\ suf[l] \% p = suf[r + 1] \% p \]

令\(suf[i]\)为\([i,n]\)数字串所形成的数字\(\%p\)后的余数

那么题目就转化为：询问在区间\([l,r]\)中二元组\((i,j)\)，满足\(suf[i] = suf[j + 1]\)的个数

显然可以用莫队解决，注意\(p\leq10^9\)，所以需要对\(suf[i]\)进行离散化

  • 当\(p = 2 \ or \ 5\)的时候考虑特判

显然如果一个数字串结尾的数字\(\%p=0\)，那么那么该数字前面的包含该数字的子串都是\(p\)的倍数

所以如果\(s[i]\%p=0,i \in[l,r]\)，那么第\(i\)位数字对答案的贡献为\(i - l + 1\)

所以对于一个区间的询问，我们考虑预处理前缀答案以及前缀个数即可

const int N = 2e5 + 10, M = 4e5 + 10;
const int B = sqrt(N) + 1;

int n, p, q, pre1[N], pre2[N], suf[N];
int id[N], ans[N], preAns, cnt[N];
string s;

struct QUERY
{
    int l, r, idx;
    bool operator<(const QUERY &t) const
    {
        if (id[l] == id[t.l])
        {
            if (id[l] & 1)
                return r < t.r;
            else
                return r > t.r;
        }
        else
            return l < t.l;
    }
} qry[N];

void build()
{
    for (int i = 1; i <= n + 1; ++i)
        id[i] = (i - 1) / B + 1;
}

void del(int i)
{
    cnt[suf[i]]--;
    preAns -= cnt[suf[i]];
}

void add(int i)
{
    preAns += cnt[suf[i]];
    cnt[suf[i]]++;
}

void cal()
{
    for (int i = 1; i <= n; ++i)
    {
        if ((s[i] - '0') % p == 0)
        {
            pre1[i] = pre1[i - 1] + i;
            pre2[i] = pre2[i - 1] + 1;
        }
        else
        {
            pre1[i] = pre1[i - 1];
            pre2[i] = pre2[i - 1];
        }
    }
    cin >> q;
    while (q--)
    {
        int l, r;
        cin >> l >> r;
        int res = pre1[r] - pre1[l - 1];
        cout << res - (pre2[r] - pre2[l - 1]) * (l - 1) << endl;
    }
}

void solve()
{
    cin >> p >> s;
    n = s.length();
    s = " " + s;
    // p = 2 or 5 时特判
    if (p == 2 || p == 5)
    {
        cal();
        return;
    }
    build();
    vector<int> vec;
    int pow = 1;
    suf[n + 1] = 0;
    // 最后一个点也要离散化
    vec.push_back(suf[n + 1]);
    for (int i = n; i >= 1; --i)
    {
        suf[i] = (suf[i + 1] + (s[i] - '0') * pow % p) % p;
        pow = pow * 10 % p;
        vec.push_back(suf[i]);
    }
    sort(all(vec));
    vec.erase(unique(all(vec)), vec.end());
    auto find = [&](int x)
    {
        return lower_bound(all(vec), x) - vec.begin() + 1;
    };
    for (int i = 1; i <= n + 1; ++i)
        suf[i] = find(suf[i]);
    cin >> q;
    for (int i = 1; i <= q; ++i)
    {
        int l, r;
        cin >> l >> r;
        qry[i] = {l, r + 1, i};
    }
    sort(qry + 1, qry + q + 1);
    for (int i = 1, l = 1, r = 0; i <= q; ++i)
    {
        while (l > qry[i].l)
            add(--l);
        while (r < qry[i].r)
            add(++r);
        while (l < qry[i].l)
            del(l++);
        while (r > qry[i].r)
            del(r--);
        ans[qry[i].idx] = preAns;
    }
    for (int i = 1; i <= q; ++i)
        cout << ans[i] << endl;
}

标签：suf,idx,int,++,while,qry,莫队
From： https://www.cnblogs.com/Zeoy-kkk/p/17658667.html

相关文章

  • 重拾莫队的一点儿思考
    发现在过去一年里好多东西都忘光了，于是全部重来。对于最简单的一个莫队情景：序列长度为\(n\)，有\(q\)次询问，插入、删除复杂度均为\(O(1)\)。我们把询问按照左端点排序，然后分块，每一块内再按照右端点来排序……等一等？考虑一下两种不同的分块方式。第一种，把原序列按\(B\)分块......
  • 莫队学习笔记
    学习莫队是非常有必要的众所周知，莫队是一种优越的暴力算法，当我们在\(NOIP\)等考试中数据结构不会打且问题是离线时，我们就可以：莫队，启动！好，切入正题，我们现在来看看莫队是什么：例题传送门简要题意：给定一个长度为\(n\)的序列\(a\)，然后再给一个数字\(k\)，再给出\(m\)组询问，每......
  • 回滚莫队 学习笔记
    板子题交\(998244353\)遍一直UKE我哭死。回滚莫队有些题看起来像个莫队，想着想着发现add操作很容易实现，而del操作怎么都想不出来，或者是del操作时间复杂度不是\(O(1)\)时间复杂度爆炸，那么回滚莫队就能派上用场。这种莫队不带删因此也叫做不带删莫队。AT_joisc2014_c......
  • Gym103687D The Profiteer：回滚莫队信息双指针可以做到线性对数
    标题写得好所谓的回滚莫队信息意思是，设信息保存在两个大小分别为\(a,b\)的结构上，将这两个信息进行合并得到大小为\(a+b\)的信息需要的时间为\(\Omega(\min\{a,b\}\cdotf(n))\)；而给定一个大小为\(1\)的信息，可以在\(\mathrmO(f(n))\)时间内将它加入到任何一个结构中......
  • 莫队
    回滚莫队++L一定要独立出来inlinevoidQ(){k=pow(n,0.66);for(inti=1;i<=max(n,m);++i)block[i]=(i-1)/k+1;for(inti=1;i<=q;++i)qwe[i]={read(),read(),read(),read(),i,0};sort(qwe+1,qwe+q+1,cmp);intL=1,R=0,las=0,_l;for(inti=1;i......
  • [Ynoi2016] 这是我自己的发明(根号分治+分块/莫队)
    题目传送门soltion简单题换根显然可以拆成\(O(1)\)个区间，这里先不管。直接做法是莫队，把双子树拆成\(dfs\)序上的双前缀，可以直接莫队，但是常数比较大。另一种做法是根分，对颜色出现次数分治，大于的求出\(dfs\)序的前缀和即可，小于的因为一共只有\(O(n\sqrtn)\)个点对，所以......
  • 普通莫队
    普通莫队形式如果从\([l，r]\)的答案能够$O(1)$扩展到\([l+1，r][l-1，r][l，r+1][l，r-1]\)（即与\([l，r]\)相邻的区间）的答案，那么使用莫队算法可以在\(O(n\sqrtn)\)的复杂度内求出所有询问的答案。核心我们假设已经知道\([l,r]\)的答案，现在我们要求\([l',r']\),我们就可以移动左右指针......
  • 莫队学习
    大致思路：1.分块2.对提问排序3.暴力处理#莫队模板```cpp#include<bits/stdc++.h>usingnamespacestd;constintN=1e6+10,M=1e6+10;inta[N],belong[N],bnum,cnt[N];intn,q,len,ans[M];structnode{ intl,r,id;}e[M];boolcmp(nodea,nodeb){ return(belong[a.l]^belong[b......
  • 莫队
    简介用于解决一类离线区间询问问题。将其加以扩展，便能轻松处理树上路径询问以及支持修改操作。普通莫队算法概述对于序列上的区间询问问题，如果从\([l,r]\)答案能够\(O(1)\)扩展到\([l-1,r],[l+1,r],[l,r+1],[l,r-1]\)（即与\([l,r]\)相邻的区间）的答案，那么......
  • 莫队学习笔记
    这是一篇模仿算导的学习笔记/题解。例题：P1494给定一个长为\(n\)的数组\(a\)和\(m\)个询问（有序数对）\(b_i=(l_i,r_i)\)，询问允许离线，对每个询问\((l,r)\)求出满足\(l\lei\ltj\ltr\wedgea_i=a_j\)的数对\((i,j)\)数量.证明：若数\(x\)在\(a\)数组下标为......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99