GNN学习 GNN理论
增强GNN的表现力
GCN=mean-pool+Linear+ReLU1
GraphSAGE=MLP+max-pool
问题:
GNN节点embedding能否区分不同节点的局部邻居结构,在什么情况下会区分失败
接下来讲GNN如何捕获局部邻居结构
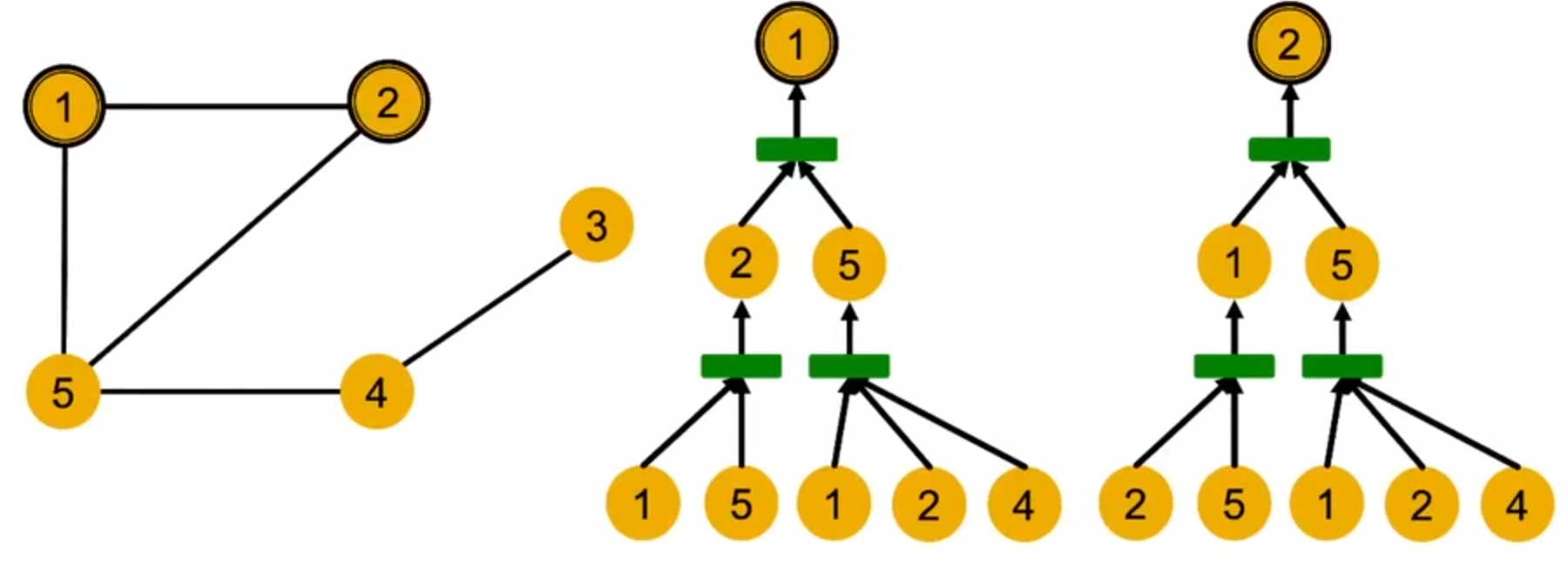
计算图
GNN每层都聚合邻居信息,通过邻居得到的计算图产生embedding
GNN只能识别特征,不能识别ID
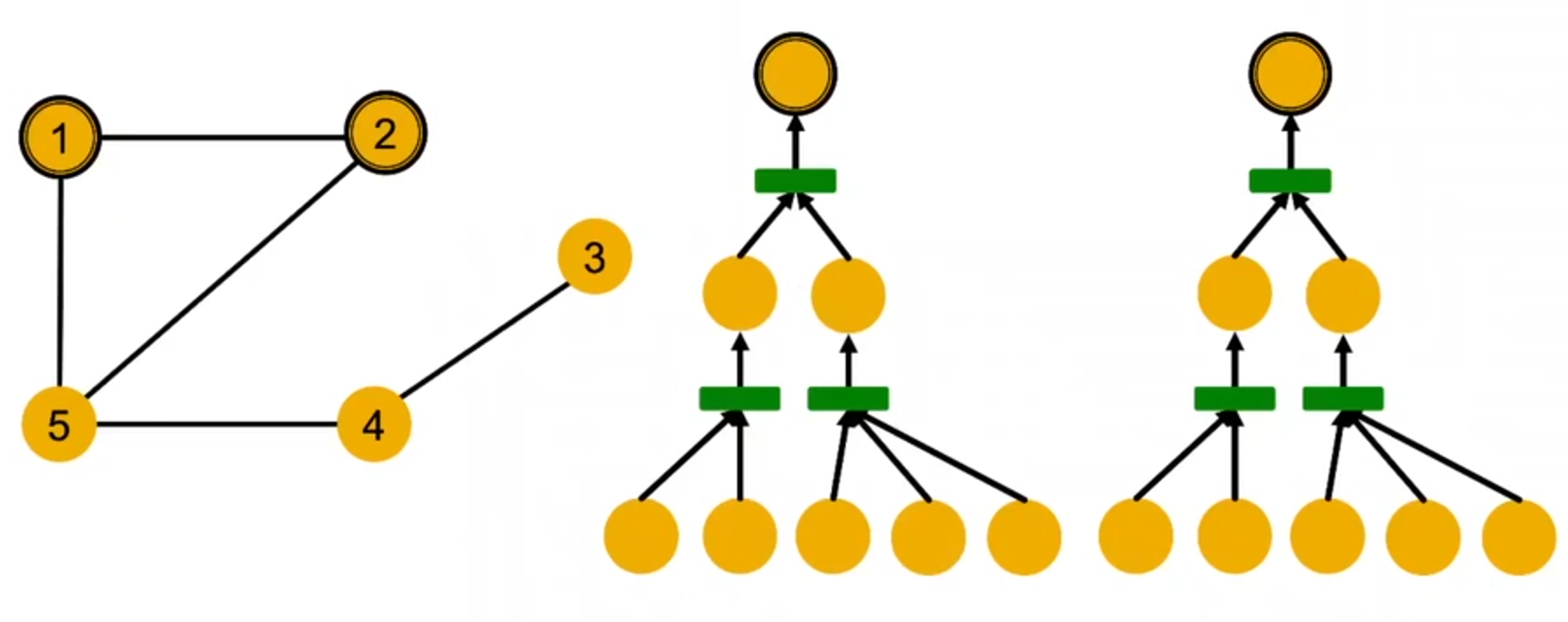
所以对GNN来说,上面的计算图等效于下面的这个计算图
一般来说,不同的局部邻居会得到不同的计算图
如果GNN给两个节点产生相同的embedding,那么是因为:
- 计算图相同
- 节点的特征也相同
计算图实际上就是节点的根子树结构
表示能力最强的GNN模型将不同的根子树结构映射到不同的节点embedding
单射函数(injective)就是将不同的自变量映射为不同的因变量
表示能力最强的GNN应该将子树映射到节点embedding以单射的形式
同深度的子树可以从叶节点到根节点迭代来表示信息并加以区分
如果GNN每一步集合都可以保留全部邻居信息,也就是每一步都使用单射的邻居聚合函数
设计表现力强的GNN
GNN的表示能力取决于其采用的邻居聚合函数,聚合函数表达能力越强,GNN的表达能力就越强
邻居聚合的过程就可以被抽象为multi-set上的函数
GCN使用的是mean-pool
GraphSAGE使用max-pool
mean-pool无法区分元素占比相同的multi-set
max-pool无法区分集合中有相同的不同的元素
GNN表示能力的总结
- GNN的表示能力由其邻居聚合函数决定
- 邻居节点的聚合是一个在multiset上的函数,multi-set是一个元素可重复的集合
- GCN和GraphSAGE的聚合函数都不能区分某些基本的multi-set,因为聚合函数都不单射,不够具有表达能力
所以,为了增强聚合函数的表达能力,我们需要用神经网络来建模单射的multi-set函数
任意一个单射的multi-set函数都可以表示为:
$ \Phi (\sum_{x \in S}f(x) ) $
其中\(\Phi\)和f都是非线性函数
那么怎样建模\(\Phi\)和f呢,我们可以采用多层感知机
于是,聚合函数就可以变成:
\(MLP_{\Phi}(\sum_{x\in S}MLP_f(x))\)
在实践中,MLP的隐藏层维度在100-500就够用了
于是就出现了一种新的GNN
Graph Isomorphism Network(GIN)
这个神经网络采用了上述的聚合函数,是信息传递类GNN中表示能力最强的GNN
接下来介绍一下WL graph kernel,这是一个经典的获取图级别特征的方法
算法:color refinement
已有一个有V个node的图G
-
给每个节点分配一个初始的颜色\(c^{(0)}(v)\)
-
不停的细化图的颜色通过\(c^{k+1}(v)=HASH(c^{(k)}(v),\{c^{(k)}(u)\}_{u\in N(v)})\)其中HASH函数将不同的输入映射到不同的颜色
-
在K步后的color refinement之后,\(c^{(K)}(v)\)总结了K-hop邻居的结构
迭代至稳定后,如果两个图的颜色集相同,则说明它们同构(isomorphic)
3.GIN
GIN就是用神经网络来模拟单射的哈希函数
\(c^{(k)}(v)\)是根节点的特征
\(\{c^{(k)}(u)\}_{u\in N(v)}\)是邻居节点的特征
所以聚合函数可以建模为
\(MLP_{\Phi}((1+\epsilon)\cdot MLP_f(c^{(k)}(v))+\sum_{u\in N(v)}MLP_f(c^{(k)}(u)))\)
其中\(\epsilon\)是一个可以训练的标量
如果节点是独热编码,那么直接加总是单射的,我们只需要\(\Phi\)来保证单射,于是
\(GINConv(c^{(k)}(v),\{c^{(k)}(u)\}_{u\in N(v)})=MLP_{\Phi}((1+\epsilon)\cdot c^{(k)}(v)+\sum_{u\in N(v)}c^{(k)}(u))\)
GIN的节点嵌入的更新过程
-
给每个节点分配初始向量\(c^{(0)}(v)\)
-
迭代更新\(c^{(k+1)}(v)=GINConv(c^{(k)}(v),\{c^{(k)}(u)\}_{u\in N(v)})\) GINConv相当于可微的color HASH函数,将不同输入映射到不同的嵌入中
-
在K步后的color refinement之后,\(c^{(K)}(v)\)总结了K-hop邻居的结构