图论
200. 岛屿数量
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
示例 2:
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 300grid[i][j]的值为'0'或'1'
class Solution {
public:
int numIslands(vector<vector<char>>& grid) {
//剪枝:空网格直接返回
if (!grid.size()) return 0;
//获取行列数
int rows = grid.size();
int cols = grid[0].size();
//初始化岛屿数
int count = 0;
//遍历所有格子
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
//如果遇到陆地('1'),则进行深度优先搜索(DFS)
//将其和其相邻的陆地全部标记为已访问(将'1'改成'0'),同时将岛屿数量加一
if (grid[i][j] == '1') {
dfs(grid, i, j);
count++;
}
}
}
return count;
}
private:
//深度优先搜索(DFS)作用:将其和其相邻的陆地全部标记为已访问(将'1'改成'0')
//参返分析:输入待遍历的表格和当前所在行列
//终止条件:
// 结构终止:当前行列超出边界
// 业务终止:遇见水
//单层逻辑:将当前格子设为水,表示已访问
void dfs(vector<vector<char>>& grid, int row, int col) {
int rows = grid.size();
int cols = grid[0].size();
if (row < 0 || row >= rows || col < 0 || col >= cols || grid[row][col] == '0') {
return;
}
//将当前格子设为水,表示已访问
grid[row][col] = '0';
//递归处理上下左右
dfs(grid, row - 1, col);
dfs(grid, row + 1, col);
dfs(grid, row, col - 1);
dfs(grid, row, col + 1);
}
};
994. 腐烂的橘子
在给定的 m x n 网格 grid 中,每个单元格可以有以下三个值之一:
- 值
0代表空单元格; - 值
1代表新鲜橘子; - 值
2代表腐烂的橘子。
每分钟,腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1 。
示例 1:
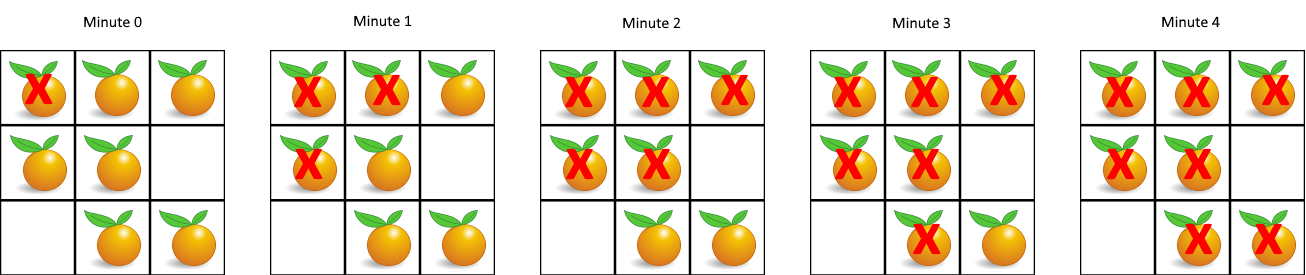
输入:grid = [[2,1,1],[1,1,0],[0,1,1]]
输出:4
示例 2:
输入:grid = [[2,1,1],[0,1,1],[1,0,1]]
输出:-1
解释:左下角的橘子(第 2 行, 第 0 列)永远不会腐烂,因为腐烂只会发生在 4 个正向上。
示例 3:
输入:grid = [[0,2]]
输出:0
解释:因为 0 分钟时已经没有新鲜橘子了,所以答案就是 0 。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 10grid[i][j]仅为0、1或2
class Solution {
public:
int orangesRotting(vector<vector<int>>& grid) {
//获取行列
int rows = grid.size();
int cols = grid[0].size();
//初始化腐烂所需天数
int days = 0;
//定义四个方向向量,用于表示上下左右四个方向(纯技巧)
//四个方向向量 {dirX, dirY} 表示了在二维平面中四个方向的移动
//其中 dirX 表示在 x 轴上的移动,dirY 表示在 y 轴上的移动。
//例如:
//{-1, 0} 表示向上移动一格,{1, 0} 表示向下移动一格
//{0, -1} 表示向左移动一格,{0, 1} 表示向右移动一格
vector<int> dirX = {-1, 0, 1, 0};
vector<int> dirY = {0, -1, 0, 1};
//初始化队列,遍历所有格子,将所有腐烂的橘子加入队列
queue<pair<int, int>> rottenQueue;
for(int i = 0; i < rows; i++) {
for(int j = 0; j < cols; j++) {
if(grid[i][j] == 2) {
rottenQueue.push({i, j});
}
}
}
//形似层序遍历
while(!rottenQueue.empty()) {
int size = rottenQueue.size();
for(int i = 0; i < size; i++) {
pair<int, int> point = rottenQueue.front();
rottenQueue.pop();
//获取烂橘子坐标
int x = point.first, y = point.second;
// 腐烂周围的新鲜橘子,引入 dirX 和 dirY 以后,就能用一个 for 循环表示四种移动
for(int j = 0; j < 4; j++) {
int newX = x + dirX[j];
int newY = y + dirY[j];
// 若周围的位置合法且为新鲜橘子,则标记为腐烂橘子,并将其加入队列
if(newX >= 0 && newX < rows && newY >= 0 && newY < cols
&& grid[newX][newY] == 1) {
grid[newX][newY] = 2;
rottenQueue.push({newX, newY});
}
}
}
if(!rottenQueue.empty()) { // 还有新的腐烂橘子,增加一天
days++;
}
}
// 检查是否还有新鲜橘子
for(int i = 0; i < rows; i++) {
for(int j = 0; j < cols; j++) {
if(grid[i][j] == 1) {
return -1;
}
}
}
return days;
}
};
207. 课程表
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
- 例如,先修课程对
[0, 1]表示:想要学习课程0,你需要先完成课程1。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:true
解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
示例 2:
输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
输出:false
解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
提示:
1 <= numCourses <= 20000 <= prerequisites.length <= 5000prerequisites[i].length == 20 <= ai, bi < numCoursesprerequisites[i]中的所有课程对 互不相同
本质上就是拓扑排序判断是否成环,用深度优先搜索(DFS)来实现拓扑排序,纯技巧,可作为原子操作
class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
// 构建图的邻接表表示
vector<vector<int>> graph(numCourses);
for (auto& p : prerequisites) {
graph[p[0]].push_back(p[1]);
}
// 记录每个节点的访问状态
vector<int> visited(numCourses, 0);
// 对每个节点进行深度优先搜索
for (int i = 0; i < numCourses; ++i) {
if (!dfs(graph, visited, i)) {
return false;
}
}
return true;
}
bool dfs(vector<vector<int>>& graph, vector<int>& visited, int cur) {
// 如果当前节点已被访问,说明存在环,返回 false
if (visited[cur] == 1) {
return false;
}
// 如果当前节点已被其他节点访问,无需重复搜索,直接返回 true
if (visited[cur] == -1) {
return true;
}
// 设置当前节点为已访问
visited[cur] = 1;
// 搜索当前节点的邻居节点
for (int neighbor : graph[cur]) {
if (!dfs(graph, visited, neighbor)) {
return false;
}
}
// 回溯,将当前节点设置为已访问其他节点
visited[cur] = -1;
return true;
}
};
208. 实现 Trie (前缀树)
Trie(发音类似 "try")或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
Trie()初始化前缀树对象。void insert(String word)向前缀树中插入字符串word。boolean search(String word)如果字符串word在前缀树中,返回true(即,在检索之前已经插入);否则,返回false。boolean startsWith(String prefix)如果之前已经插入的字符串word的前缀之一为prefix,返回true;否则,返回false。
示例:
输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]
解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 True
trie.search("app"); // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app"); // 返回 True
提示:
1 <= word.length, prefix.length <= 2000word和prefix仅由小写英文字母组成insert、search和startsWith调用次数 总计 不超过3 * 104次
类似于 LRU,纯技巧构造数据结构
class TrieNode {
public:
bool is_end; // 标记当前节点是否是一个单词的结尾
TrieNode* children[26]; // 存放所有可能的字母子节点
TrieNode() {
is_end = false; // 默认不是单词结尾
for (int i = 0; i < 26; ++i) {
children[i] = nullptr; // 初始化子节点为空指针
}
}
};
class Trie {
public:
TrieNode* root; // 根节点
Trie() {
root = new TrieNode(); // 创建一个空的trie树,只有一个根节点
}
void insert(string word) {
TrieNode* node = root; // 从根节点开始
for (int i = 0; i < word.length(); ++i) { // 遍历单词的每个字母
int index = word[i] - 'a'; // 计算字母的索引(a-z对应0-25)
if (node->children[index] == nullptr) { // 如果子节点为空,表示以当前字母开头的单词还没有加入trie树
node->children[index] = new TrieNode(); // 创建一个新的子节点
}
node = node->children[index]; // 继续进入下一个字母的子节点
}
node->is_end = true; // 将最后一个字母所在节点标记为单词结尾
}
bool search(string word) {
TrieNode* node = root; // 从根节点开始
for (int i = 0; i < word.length(); ++i) { // 遍历单词的每个字母
int index = word[i] - 'a'; // 计算字母的索引(a-z对应0-25)
if (node->children[index] == nullptr) { // 如果子节点为空,表示以当前字母开头的单词不存在
return false;
}
node = node->children[index]; // 继续进入下一个字母的子节点
}
return node->is_end; // 判断最后一个字母所在节点是否是一个单词的结尾
}
bool startsWith(string prefix) {
TrieNode* node = root; // 从根节点开始
for (int i = 0; i < prefix.length(); ++i) { // 遍历前缀的每个字母
int index = prefix[i] - 'a'; // 计算字母的索引(a-z对应0-25)
if (node->children[index] == nullptr) { // 如果子节点为空,表示以当前字母开头的单词不存在
return false;
}
node = node->children[index]; // 继续进入下一个字母的子节点
}
return true; // 前缀匹配成功
}
};
回溯
46. 全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1]
输出:[[1]]
提示:
1 <= nums.length <= 6-10 <= nums[i] <= 10nums中的所有整数 互不相同
回溯三部曲
回溯法可解决问题都可抽象为树,回溯的本质是优雅地枚举
- for 循环:横向遍历可以做出的选择
- 递归:纵向遍历,表示做出选择后的状态转移
- 参返分析:回溯返回值一般为 void,带放回,引入标记已选择元素的 used 数组作参数,同时需要将元素集合作参数
- 终止条件:如果路径的长度等于数组的长度,说明已经找到一个符合条件的结果
- 遍历过程:带放回,故每层都从 0 开始搜索,需要引入 used 数组作为已选择标记。回溯每一个位置可以选择的数字
- 递归
- 如果该数字已经被使用过,继续查找下一个数字
- 如果该数字未被使用过,标记该数字已经使用过,将该数字加入路径中
- 回溯
- 将数字移出路径
- 将数字的访问标记去除
- 递归
class Solution {
public:
//存放符合条件的所有结果的集合
vector<vector<int>> res;
//存放符合条件的单一结果
vector<int> path;
void backtrack(vector<int>& nums, vector<bool>& used){
// 如果路径的长度等于数组的长度,说明已经找到一个符合条件的结果,将其加入结果集合中
if(path.size() == nums.size()){
res.push_back(path);
return;
}
// 回溯每一个位置可以选择的数字
for(int i = 0; i < nums.size(); i++){
// 如果该数字已经被使用过,继续查找下一个数字
if(used[i]) continue;
// 标记该数字已经使用过
used[i]=true;
// 将该数字加入路径中
path.push_back(nums[i]);
// 开始对剩下的数字进行回溯
backtrack(nums, used);
// 回溯完之后,需要将该数字从路径中移除,并取消标记
path.pop_back();
used[i]=false;
}
}
vector<vector<int>> permute(vector<int>& nums) {
// 初始化所有数字的使用情况,默认为false表示未使用过
vector<bool> used(nums.size(), false);
// 开始回溯
backtrack(nums, used);
return res;
}
};