题意分析
我们首先想到,枚举贝茜在 \(x\) 点,枚举度数大于 \(2\) 的点为 \(y\)。设 \(x\) 的度数为 \(a\),\(y\) 的度数为 \(b\)。
我们首先发现每个 \(x\) 点都有一个初始的贡献为 \(a\) 条通往叶子的路径。
如果点 \(y\) 到最近的叶子节点的距离大于到 \(x\) 的点的距离(农夫不能在 \(y\) 点追上贝茜),则 \(y\) 点可以贡献额外的 \(b-2\) 条路径。(\(y\) 的度数减去进入 \(y\)、离开 \(y\) 的初始贡献消耗的度数)。
我们考虑先预处理出每个 \(y\) 点到最近的叶子节点的距离为 \(mi_y\)。
void bfs(int x){
queue<pair<int,int> >q;
q.push(make_pair(x,0));
bool v[70010]={};
while(!q.empty()){
int y=q.front().first,z=q.front().second;
q.pop();
for(int i=hea[y];i;i=nex[i]){
int t=to[i];
if(v[t]!=1){
v[t]=1;
if(siz[t]==1){
mi[x]=z+1;
return;
}
q.push(make_pair(t,z+1));
}
}
}
}
然后再从 \(x\) 点搜索出所有的 \(y\) 点计算出合法贡献。注意不能加上自己。
void dfs(int x,int nu,int fa){
if(siz[x]>2){
if(nu<mi[x]&&nu!=0) ans+=siz[x]-2;
tot++;
}
if(tot>=num) return ;
for(int i=hea[x];i;i=nex[i]){
int t=to[i];
if(t!=fa){
dfs(t,nu+1,x);
}
}
}
我们发现这样会 TLE \(5\) 个点。
我们考虑优化,我们发现枚举的 \(x\) 点数量太多。我们可以枚举 \(y\) 点反推 \(x\) 点。
像这样:
void bf(int x){
queue<pair<int,int> >q;
q.push(make_pair(x,0));
bool v[70010]={};
while(!q.empty()){
int y=q.front().first,z=q.front().second;
q.pop();
if(y!=x)
an[y]+=siz[x]-2;
if(z+1<mi[x])
for(int i=hea[y];i;i=nex[i]){
int t=to[i];
if(v[t]!=1){
v[t]=1;
q.push(make_pair(t,z+1));
}
}
}
}
证明一下复杂度:
我们考虑最坏复杂度,此时树为一棵满二叉树。
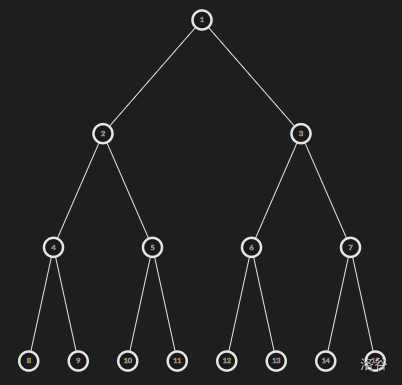
我们设树总共有 \(m\) 层。
第 \(1\) 层不会遍历。
第 \(2\) 层有 \(2^{2-1}\) 个数,每个数会遍历 \(2^{m-1}-1+1\) 次。
有什么规律呢?
我们把向上的部分转移位置,例如 \(2\) 号节点是这样的:
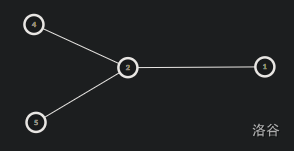
如果有更多节点,图就变成了这样。
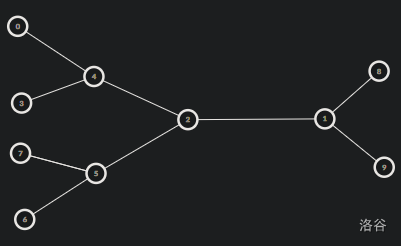
对于第 \(i\) 层遍历了 \(2^{i-1}\times(2^{m-i}-1+2^{m-i-1})\) 次。
化简一下并去掉常数就是 \(2^{m-1}\times2^{m-2}=3\times{2^{m-2}}\) 次。
由于是一个满二叉树,节点数 \(n=2^m-1\),\(m\approx{log(n)}\)。
所以复杂度就是 \(m\times{\tfrac{3}{4}\times{2^m}}\approx{O(n\log{n})}\)。
由于常数较小,故比点分治快。
code
#include<iostream>
#include<queue>
#include<cstdio>
#include<utility>
using namespace std;
int n,siz[70010],mi[70010],num,ans,ma;
int tot,hea[70010],nex[200010],to[200010],an[70010];
void add(int x,int y){
to[++tot]=y;
nex[tot]=hea[x];
hea[x]=tot;
}
void bfs(int x){
queue<pair<int,int> >q;
q.push(make_pair(x,0));
bool v[70010]={};
while(!q.empty()){
int y=q.front().first,z=q.front().second;
q.pop();
for(int i=hea[y];i;i=nex[i]){
int t=to[i];
if(v[t]!=1){
v[t]=1;
if(siz[t]==1){
mi[x]=z+1;
return;
}
q.push(make_pair(t,z+1));
}
}
}
}
void bf(int x){
queue<pair<int,int> >q;
q.push(make_pair(x,0));
bool v[70010]={};
while(!q.empty()){
int y=q.front().first,z=q.front().second;
q.pop();
if(y!=x)
an[y]+=siz[x]-2;
if(z+1<mi[x])
for(int i=hea[y];i;i=nex[i]){
int t=to[i];
if(v[t]!=1){
v[t]=1;
q.push(make_pair(t,z+1));
}
}
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<n;i++){
int x,y;
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
siz[x]++;
siz[y]++;
}
for(int i=1;i<=n;i++){
if(siz[i]>2){
bfs(i);
num++;
ma=max(ma,mi[i]);
}
}
for(int i=1;i<=n;i++){
if(siz[i]>2){
bf(i);
}
}
for(int i=1;i<=n;i++){
if(siz[i]==1){
printf("1\n");
}
else{
ans=siz[i];
tot=0;
printf("%d\n",ans+an[i]);
}
}
return 0;
}