圆方树

为什么只写圆方树呢，因为点双代码比圆方树长一倍

其实是因为边双可以被圆方树表示出来

前言

这里给 tarjan 中的 low 数组的定义明确一下，其代表的是包括自己在内的搜索子树内经过最多一条非树边能够到达的最浅节点

边双

这个很简单，如果有一个点的 low 值等于他的 dfn 序了，那它和栈里剩下的点就形成了一个边双

值的注意的是，对于点双和边双，因为无向图的缘故，导致点有可能会返回自己的父亲，所以尽量使用前向星存图判掉这种情况

这里贴一个板子

void tarjan_e(int now,int eid){
	low[now]=dfn[now]=++idx;
	s.push(now);
	for(int i=g.begin(now);i;i=g.nex(i))
		if(!dfn[g.to(i)]) tarjan_e(g.to(i),i),low[now]=min(low[now],low[g.to(i)]);
		else if(eid^1^i) low[now]=min(low[now],dfn[g.to(i)]);
	if(dfn[now]^low[now]);
	else {
		int u;++co;
		do u=s.get(),col[u]=co,rep[u]=now;
		while(u^now);
	}
}

点双

点双就相对复杂了，因为一个点很有可能在多个点双中存在，所以要分别处理，导致点双的代码十分复杂

所以，就要请出主角，圆方树了，其能够有效处理点双，乃至边双的问题

圆方树

顾名思义，圆方树分为圆点点和方点，圆点是原本图上的点，而方点代表一个点双，与其相连的点都是在同一个点双里面的

拿一张图：

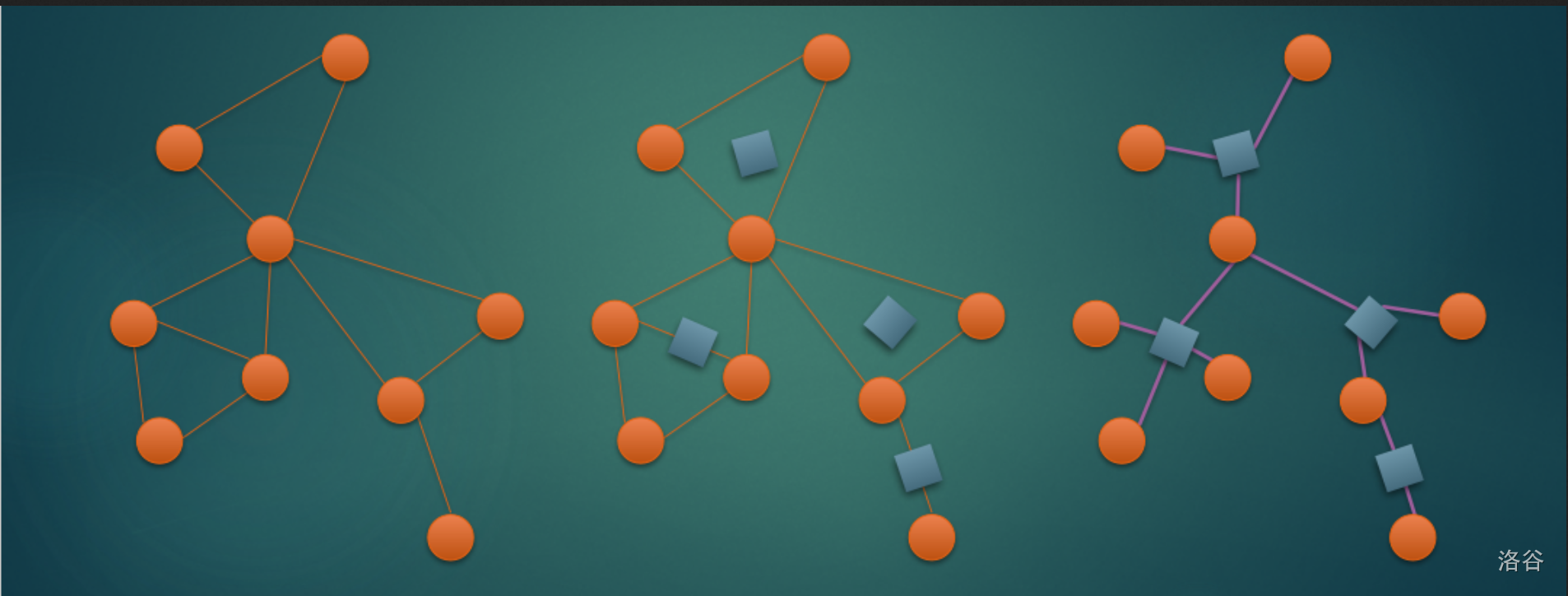
经典

那判点双就是小菜一碟了，任何不是叶子的圆点都是割点

贴一个代码

void genshin(int now){
	dfn[now]=low[now]=++idx;
	s.push(now);
	for(int i=g.begin(now);i;i=g.nex(i))
		if(!dfn[g.to(i)]){
			genshin(g.to(i)); low[now]=min(low[now],low[g.to(i)]);
			if(low[g.to(i)]^dfn[now]);
			else {
				ng.add(now,++np);
				do ng.add(np,s.top());
				while(s.get()^g.to(i));
			}
		}
		else low[now]=min(low[now],dfn[g.to(i)]);
}

这里解释一个点，为什么写不等于就可以，是因为在无向图中，我们没有判掉返回父亲这个操作，所以儿子的 low 最深也是父亲

能不能再给力一点啊

其实，圆方树完全支持维护割边，在一道极其恶心的题中，我通过翻阅最大空间的提交才懂得了如何实现，下面进行讲解

首先，每一条割边的形态都类似下图：

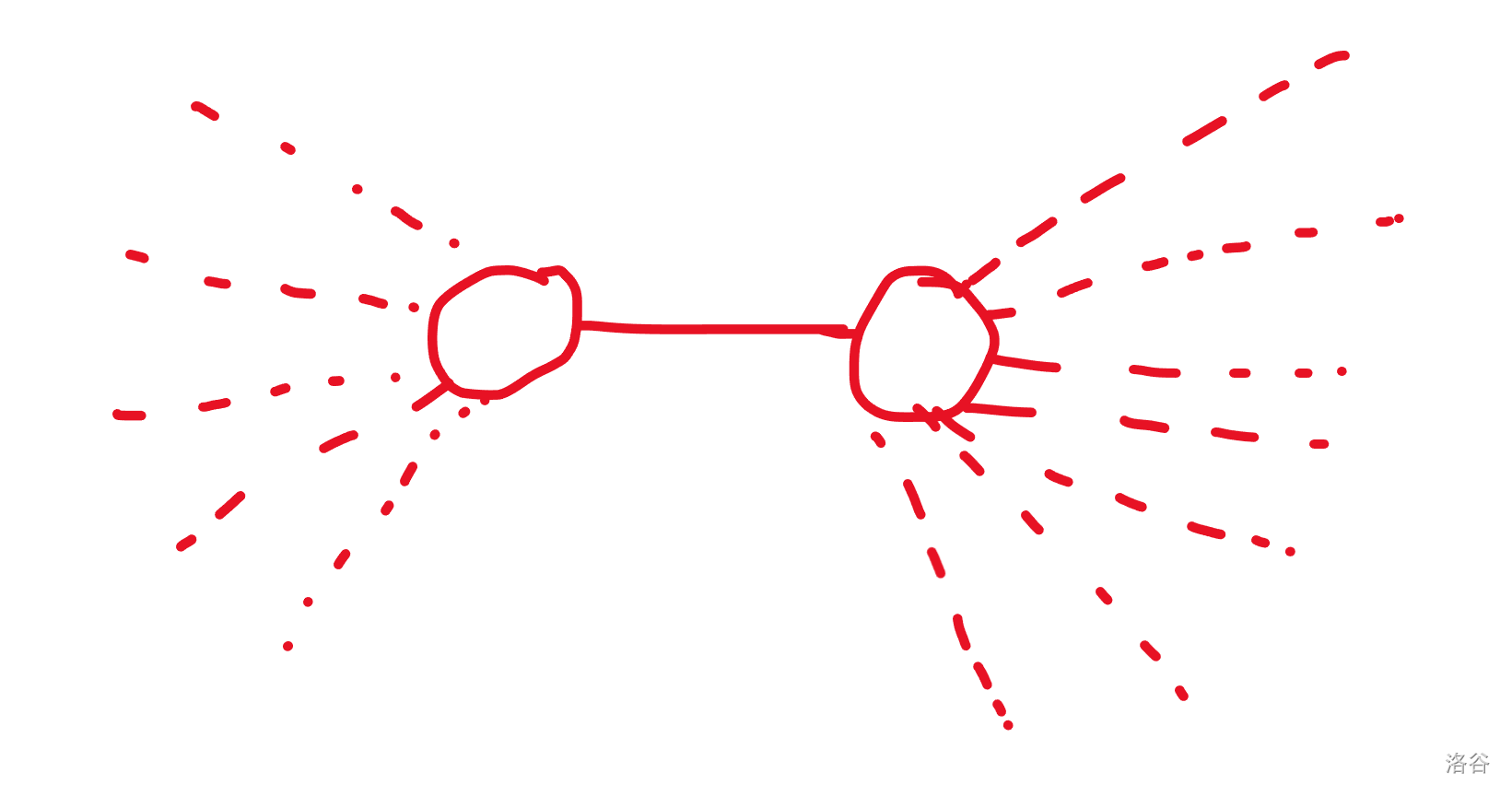
不难看出，对于割边两边的点，其一定能够构成一个点双，换句话说，这两个点一定会通过一个方点相连，我们完全可以将割边映射到这个点上去，在一些割边和割点都要维护的题中，这种方法有奇效

这里附一份代码

void genshin(int now,int eid){
	dfn[now]=low[now]=++idx;
	s.push(now);
	for(int i=g.begin(now);i;i=g.nex(i))
		if(!dfn[g.to(i)]){
			genshin(g.to(i),i); low[now]=min(low[now],low[g.to(i)]);
			if(low[g.to(i)]<=dfn[now]){
				ng.add(now,++np);
                if(low[g.to(i)]<dfn[now]) id[i]=id[i^1]=np;
				do ng.add(np,s.top());
				while(s.get()^g.to(i));
			}
		}
		else if(i^1^eid)low[now]=min(low[now],dfn[g.to(i)]);
}

就加了几行

圆方树使用的范围是有关图的连通性的，这里给几道例题，但是最关键的是一件事，一个点只能走一遍

CF487E

典中典

明显，不能重复走一条路，就建出圆方树来，我们从一个割点走到另一个割点，期间经过的点双中的任何一个点都可以找到一条路径经过，所以与一个方点相连的点中找一个最大的就可以了

对于这一类维护一圈点的问题，只要不维护父亲，怎么乱搞都是对的

一九八四

私题

给一个无向图，询问是否可以不经过一条边或者一个点而联通\(x\) 和 \(y\)

这就是经典扩展圆方树了，把割边映射到点上，两两判一下 lca 就可以了

luogu讨论区的题

给定一个无向图以及三个点 \(s,a,b\) ,求是否存在一条路径从 \(s\) 开始，经过 \(a,b\) 两点而不经过重复的点

明显的圆方树，如果这个 \(s\) ，在 \(a\) 和 \(b\) 的路径中间或者三点不在一条链上，那明显不行，这个可以通过一些树论小技巧求 lca 做到单 \(\log\) ，当然放弃思考也可以染色做到相同复杂度