线段相交Ⅲ

描述

线段相交有两种情形：一种是“规范相交”，另一种是“非规范相交”。规范相交是指两条线段恰有唯一一个不是端点的公共点。即如果一条线段的端点在另一条线段上则不视为相交。如果两条线段有部分重合，也不视为相交。而非规范相交则把以上两种情况都视为相交。如下图所示：

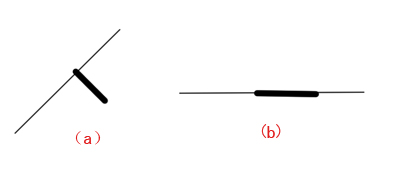
规范相交认为a，b两种情况都是不相交的，而非规范相交认为a，b两种情况都是相交的。

本题要求判断两条线段是否相交。如果是规范相交则输出YES，并输出交点坐标，如果是非规范相交则只需输出YES，如果不相交则输出NO。

输入

输入有多组数据，T表示输入数据的组数。每组测试数据有两行第一行输入一条线段的两个端点的坐标，第二行输入另一个线段的两个端点的坐标。

输出

对于每组测试数据，输出一行。如果是规范相交则输出YES，并输出交点坐标（小数点后面保留3位），如果是非规范相交则只需输出YES，如果不相交则输出NO。

样例输入

4
0 0 1 1
0 1 1 0
0 0 2 2
2 2 3 3
0 0 2 2
1.5 1.5 3 3
0 0 1 1
2 2 3 3

样例输出

YES (0.500,0.500)
YES
YES
NO

分类讨论,考虑斜率存不存在和共线平行的情况,一般情况直接算出交点,判断是否在两个线段内

#include <bits/stdc++.h>
using namespace std;
struct d
{
    double x,y;
};
int judge(d t,d a1,d a2,d b1,d b2)//2为规范相交,1为非规范相交,0为不相交
{
    if(t.x>min(b1.x,b2.x)&&t.x<max(b1.x,b2.x)&&t.y>min(b1.y,b2.y)&&t.y<max(b1.y,b2.y)&&t.x>min(a1.x,a2.x)&&t.x<max(a1.x,a2.x)&&t.y>min(a1.y,a2.y)&&t.y<max(a1.y,a2.y))//规范相交
    {
        return 2;
    }
    else if(t.x>=min(b1.x,b2.x)&&t.x<=max(b1.x,b2.x)&&t.y>=min(b1.y,b2.y)&&t.y<=max(b1.y,b2.y)&&t.x>=min(a1.x,a2.x)&&t.x<=max(a1.x,a2.x)&&t.y>=min(a1.y,a2.y)&&t.y<=max(a1.y,a2.y))//不规范相交
    {
        return 1;
    }
    else//不相交
    {
        return 0;
    }
}
signed main()
{
    int T;
    cin>>T;
    while(T--)
    {
        d a1,a2,b1,b2;
        cin>>a1.x>>a1.y>>a2.x>>a2.y>>b1.x>>b1.y>>b2.x>>b2.y;
        if((a1.y-a2.y)*(b1.x-b2.x)==(a1.x-a2.x)*(b1.y-b2.y))//平行
        {
            if(a1.x-a2.x==0)//斜率不存在
            {
                if(a1.x==b1.x)//共线
                {
                    if(judge(a1,a1,a2,b1,b2)||judge(a2,a1,a2,b1,b2))//有重叠
                    {
                        cout<<"YES"<<endl;
                    }
                    else//不重叠
                    {
                        cout<<"NO"<<endl;
                    }
                }
                else//不共线
                {
                    cout<<"NO"<<endl;
                }
            }
            else//斜率存在
            {
                double bb1=a1.y-(a1.y-a2.y)/(a1.x-a2.x)*a1.x;
                double bb2=b1.y-(b1.y-b2.y)/(b1.x-b2.x)*b1.x;
                if(bb1==bb2)//共线
                {
                    if(judge(a1,a1,a2,b1,b2)||judge(a2,a1,a2,b1,b2))//有重叠
                    {
                        cout<<"YES"<<endl;
                    }
                    else//不重叠
                    {
                        cout<<"NO"<<endl;
                    }
                }
                else//不共线
                {
                    cout<<"NO"<<endl;
                }
            }
        }
        else//不平行
        {
            if(a1.x==a2.x)//a斜率不存在
            {
                double bb2=b1.y-(b1.y-b2.y)/(b1.x-b2.x)*b1.x;
                d t={a1.x,(b1.y-b2.y)/(b1.x-b2.x)*a1.x+bb2};
                if(judge(t,a1,a2,b1,b2)==2)//规范相交
                {
                    printf("YES (%.3f,%.3f)\n",t.x,t.y);
                }
                else if(judge(t,a1,a2,b1,b2)==1)//不规范相交
                {
                    cout<<"YES"<<endl;
                }
                else//不相交
                {
                    cout<<"NO"<<endl;
                }
            }
            else if(b1.x==b2.x)//b斜率不存在
            {
                double bb1=a1.y-(a1.y-a2.y)/(a1.x-a2.x)*a1.x;
                d t={b1.x,(a1.y-a2.y)/(a1.x-a2.x)*b1.x+bb1};
                if(judge(t,a1,a2,b1,b2)==2)//规范相交
                {
                    printf("YES (%.3f,%.3f)\n",t.x,t.y);
                }
                else if(judge(t,a1,a2,b1,b2)==1)//不规范相交
                {
                    cout<<"YES"<<endl;
                }
                else//不相交
                {
                    cout<<"NO"<<endl;
                }
            }
            else//斜率都存在
            {
                double bb1=a1.y-(a1.y-a2.y)/(a1.x-a2.x)*a1.x;
                double bb2=b1.y-(b1.y-b2.y)/(b1.x-b2.x)*b1.x;
                double k1=(a1.y-a2.y)/(a1.x-a2.x);
                double k2=(b1.y-b2.y)/(b1.x-b2.x);
                d t;
                t.x=(bb2-bb1)/(k1-k2);
                t.y=k1*t.x+bb1;
                if(judge(t,a1,a2,b1,b2)==2)//规范相交
                {
                    printf("YES (%.3f,%.3f)\n",t.x,t.y);
                }
                else if(judge(t,a1,a2,b1,b2)==1)//不规范相交
                {
                    cout<<"YES"<<endl;
                }
                else//不相交
                {
                    cout<<"NO"<<endl;
                }
            }
        }
    }
}