模拟赛做到的题,场上写贪心爆栈了qwq
首先在首尾加上两个 \(1\) 表示进出,将两段路中间的间隔作为传送门,恰好有
\(2 \times N\) 个传送门,根据两段路的经过情况给传送门分类别:
00:用 \(N\) 表示,称为无用点,不到达该点。
10:用 \(S\) 表示,称为起点,需要通过向右走走到一次。
01:用 \(T\) 表示,称为终点,需要通过传送到达一次。
11:用 \(M\) 表示,称为中转点,需要分别通过向右和传送到达两次。
容易发现:中转点需要两两配对,起点和终点配对,无用点相互配对。
所以以下三种情况可以直接判无解:
- 中转点个数不为2的倍数
- 起点个数 \(\neq\) 终点个数
- 无用点个数不为2的倍数
接下来考虑具体的配对问题:
对于中转点 \(M\):考虑将连续的四个 \(M\) 以 1212 的配对方式消掉,如图所示:
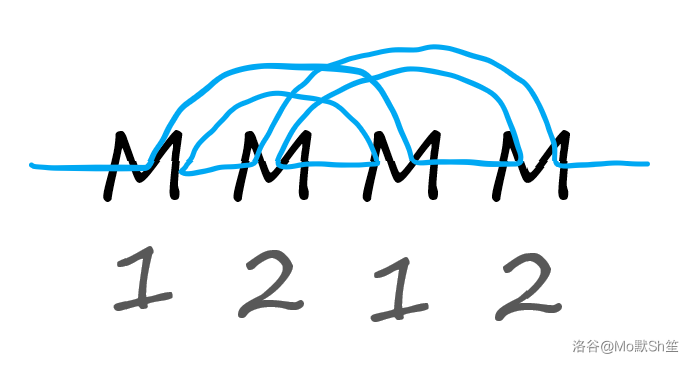
事实上不连续的四个 \(M\) 也可以这样消掉,因为 \(M\) 的左右对应的路都是 \(1\),左相邻的传送门只能是 \(T/M\),右响铃的传送门只能是 \(S/M\),也就是说两段连续的 \(M\) 之间只可能是不断重复的 \(ST\) ,将 \(ST\) 匹配消掉即可,如图所示:

综上所述:当 \(M\) 的个数是 \(4\) 的倍数时,只需要将所有 \(M\) 从左往右按照 1212 的配对方式配对即可。
当 \(M\) 的个数不为 \(4\) 的倍数时,因为 \(M\) 需要两两匹配,有解时一定为 \(2\) 的倍数,匹配时考虑将两个 \(M\) 消掉,对剩下的 \(M\) 按上面的方法匹配。
设两个 \(M\) 中位置靠前的为 \(M_{1}\),位置靠后的为 \(M_{2}\),因为无法使用更多的 \(M\),我们需要通过 \(M_{1}/M_{2}\) 所处连续段的前后的 \(T\) 和 \(S\) 让当前所处位置倒退,以此来二次经过通过传送到达的 \(M_{2}\),这样我们就用一对 \(ST\) 消掉了两个 \(M\),中间的连续的 \(M\) 与其它段的 \(M\) 结合,通过之前的方法消掉,然后会二次经过 \(M_{2}\),正好将落单的 \(ST\) 消掉,两种情况分别如图所示:
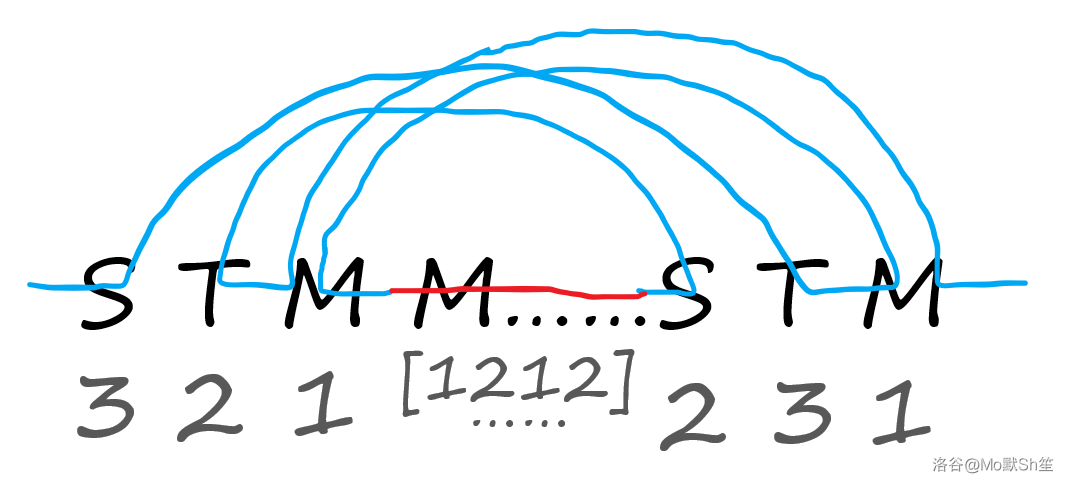

如果两种情况均不满足,比如 MSTM 的情况,判成无解。
细节:因为此时的配对起始位置发生了改变,所以将剩下的 \(M\) 消掉时不能像之前一直接样从左往右,要先记录中间段的 \(M\),再对剩下未匹配的 \(M\) 从左往右记录进行配对。
对于剩下未匹配的 \(S\) 和 \(T\) 和 \(N\) ,直接找到右边第一个还未匹配的对应匹配即可。
时间复杂度:\(\mathcal{O}(n)\)
\(\mathcal{Code}\):
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define db double
#define il inline
#define re register
#define INF 0x3f3f3f3f
#define LINF 0x3f3f3f3f3f3f3f3f
#define F(i,a,b) for(int (i)=(a);(i)<=(b);(i)++)
#define DF(i,a,b) for(int (i)=(a);(i)>=(b);(i)--)
#define G(i,u) for(int (i)=head[u];(i);(i)=nxt[(i)])
inline ll read(){ll x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-48;ch=getchar();}return x*f;}
const int N=200010;
int n,num,tot;
char str[N];
int a[N],t[N],c[N];//1:st 2:nd 3:st+nd
int M[N];
int main()
{
n=read()<<1;
scanf("%s",str);
F(i,1,n-1) a[i]=str[i-1]-'0';
a[0]=a[n]=1;
int cntS=0,cntT=0,cntM=0;
F(i,1,n)
{
if(a[i-1]==1&&a[i]==0) t[i]=1,cntS++;
if(a[i-1]==0&&a[i]==1) t[i]=2,cntT++;
if(a[i-1]==1&&a[i]==1) t[i]=3,cntM++;
}
if(cntS!=cntT||cntM%2)//判无解
{
printf("No");
return 0;
}
int lstL=0,lstR=0,flag=0;
if(cntM%4)
{
for(int l=1,r=1;l<=n;l=r)
{
while(t[r]==3&&r<=n) r++;
r--;//方便记录区间
if(lstL&&lstR)
{
if(t[l-1]==2&&t[r+1]==1)//右边有S+T
{
c[lstL]=c[r]=++num;
c[l-1]=c[r+1]=++num;
flag=1;
}
else if(t[lstL-1]==2&&t[lstR+1]==1)//右边无S+T,左边有S+T
{
c[l]=c[lstR]=++num;
c[lstL-1]=c[lstR+1]=++num;
flag=1;
}
F(i,l,r)//因为起始点变化了,要先将中间段推入数组
if(!c[i]&&t[i]==3)
M[++tot]=i;
lstL=l,lstR=r;
break;
}
else lstL=l,lstR=r;
r++;//归位
while(t[r]!=3&&r<=n) r++;
}
if(!flag)//判无解
{
printf("No");
return 0;
}
}
F(i,1,lstL-1)//挖去中间段,对剩下块统计
if(!c[i]&&t[i]==3)
M[++tot]=i;
F(i,lstR+1,n)//挖去中间段,对剩下块统计
if(!c[i]&&t[i]==3)
M[++tot]=i;
int lstS=0,lstT=0,lstN=0;
F(i,1,n)//对剩下的进行统计
{
if(c[i]) continue;
if(t[i]==1)
{
if(lstT) c[i]=c[lstT]=++num,lstT=0;
else lstS=i;
}
else if(t[i]==2)
{
if(lstS) c[i]=c[lstS]=++num,lstS=0;
else lstT=i;
}
else if(!t[i])
{
if(lstN) c[i]=c[lstN]=++num,lstN=0;
else lstN=i;
}
}
for(int i=1;i<=tot;i+=4)//对剩下的M进行匹配
{
c[M[i]]=c[M[i+2]]=++num;
c[M[i+1]]=c[M[i+3]]=++num;
}
printf("Yes\n");
F(i,1,n)
printf("%d ",c[i]);
return 0;
}