首页 > 其他分享 >MST 题单

MST 题单

时间：2023-08-06 17:48:55浏览次数：38  
标签：10 val int MST 最小 生成 edge 题单

……好多题单的题目都没补掉捏（

如何求 MST

Kruskal

MST 就是最小生成树啦~然后我发现自己最小生成树学的也不好，连夜加急八百里复习了 kruskal 和 Prim。下面简单来讲讲这两个算法吧 awa。

Kruskal 是非常简单的算法，它是怎么做的嘞？首先对所有边按照边权从大到小排个序，然后每次取出边权最小的边，如果两个端点已经连通就不合并了，否则就合并（这是为了防止出现环）。用并查集维护连通性，时间复杂度 \(O(m\log_2m)\)。非常简单的做法，我们也很容易证明它的正确性。

这基于这样一个定理：一个最小生成树一定包含当前图中最小的边。用反证法，假设最小生成树不包含当前最小的边，那么加入最小的边一定会构成一个环，环上所有的边肯定都不会比它小，我们完全可以把它替换，这样生成树会变小/不变。

我们还可以得到一个推论：对于一张图 \(G\)，假设我们用了 \(k\) 条边已经完成了最小生成的森林，然后我们加入剩下的边中的 \(n - k - 1\) 条边，使得边权和最小，那么 \(m - k\) 条边中连接森林中两棵不同的树的最小边一定会被选。把每棵树缩成一个大点就容易得到了。

基于这个推论，我们就可以得到 kruskal。我们也很容易弄清楚 kruskal 的本质了——起初是 \(n\) 个互不干涉的点，中间每个局面都是一个森林（初始盘面的 \(n\) 个孤立的点其实也不是不能看成森林），每次都可以选一条边，连接两棵树，最后变成一棵树。

Prim

Prim 算法又是什么嘞？Prim 算法也不难。首先我们达成共识这是一张连通图。以 \(1\) 为生成树的根，维护集合 \(S\) 为已经最小生成树的点，每次都找与 \(S\) 最近的没加入 \(S\) 的点，加入 \(S\)（也就是算进了最小生成树），然后更新其它点与 \(S\) 的最近距离。

这样是不是也很简单，而且和 Dijkstra 有异曲同工之妙？所以我们也可以用相似的方法证明 Prim：归纳。把每次加入的边定向成从父亲到儿子的边，\(1\) 号点肯定能选，因为它是根没有父亲，所以权值是 \(0\)。然后归纳，我们要证明对于集合 \(S\)，与其相邻的最近的边一定在最小生成树中，我们记这条边为 \((u, v, w)\)（\(u\) 在 \(S\) 内，\(v\) 不在）。我们一定可以想到使用上面的定理：把 \(S\) 里面的点构成了一棵树，然后剩下的孤立点我们一起看成一个森林。连接两个不同森林的最小边（就是这个 \((u, v, w)\)）则一定在最小生成树里面。Prim 时间复杂度 \(O(n^2)\)。当然它可以堆优化但是堆优化就变成了 \(O((m+n)\log_2 n)\) 了那么我还不如去搓一个 Kruskal。代码下面会贴，这里就不写了（

总结

所以，Kruskal 适用于稀疏图，Prim 适用于稠密图。反正我基本上没见过别人稀疏图写 Prim 的(*/ω＼*）OI 中 \(n, m\) 通常同阶，也就是稀疏图，所以大部分人都选择好写的 Kruskal。但是 Prim 也蛮重要的毕竟我今天才看到一道题目完全图必须得用 Prim（呜呜呜当时一直在想 \(O(k^2\log_2 n)\) 这也跑不过去啊没想到是 Prim（

MST 与它的一些性质和小小延伸

最小生成树的算法是不是十分的简单？qwq

那么就一起来看看一些有趣的东西吧~

最小生成树性质：

  1. 最小生成树也是原图的一棵最小瓶颈树。
    最小瓶颈树是啥？最小瓶颈树就是最大边权最小的生成树。
    证明：我们可以从小到大不断加入边，就像 Kruskal 一样，如果两端连通就不加入。最后就得到了最小生成树。很显然，这是最大边权最小的。但是这并不大严谨——在 Kruskal 的过程中我们会有一些边两端被加入过一个连通块，不能选，那么我们能不能通过扔掉本来选的边，然后省几条被扔掉的，构成更小的瓶颈树？不行，因为一条边只会连通两个连通块，每次顶多省一条边，如果省两条边就说明两个连通块里面有多条边连着，那就不叫生成树了。省一条边还不如用边权小的。
  2. 给定无向图两点 \(u,v\)，若要让 \(u\) 到 \(v\) 的路径最长边最短，那么沿着最小瓶颈路的路径上走就是最优方案的一种。
    证明：我们可以从小到大加入所有边，直到 \(u, v\) 连通……好像也是 Kruskal。
  3. 如果不断给图加边，原来不在最小生成树中的边仍然不在。证明见下。

一些与最小生成树有关的问题：

  1. 增量最小生成树：从 \(n\) 点空图开始，依次加入 \(m\) 条带权边，求出每时每刻图中最小生成树权值。若图不连通，输出无解。

解法：当图刚好连通的时候先跑一遍 kruskal，然后每次新增一条边，最小生成树上都会多出一个环。每次试着用新的边替换掉环上最大的边，如果边权变小就换掉。为什么这是对的？因为如果之前边 \(edge\) 不在最小生成树里面，之后也不会在。我们回顾一下 Kruskal 的过程，什么时候 \(edge\) 无法加入？两端点都在同一个连通块内。加入了 \((u, v, w)\) 后呢？根据 Kruskal，拍完序后 \(edge\) 排名不可能考前反而可能靠后，之前都没被加入，靠后了就更不可能加入了。这是一个很有用的性质。

  1. 每对节点之间的最小瓶颈路：\(q\) 次询问询问 \((u,v)\) 之间的最小瓶颈路中最大边长度。

解法：我们既然已经知道了它是在最小瓶颈树上的路径上，那么我们就不妨设 \(f(u, v)\) 为从 \(u\) 到 \(v\) 的最小瓶颈路，然后大力 dfs 一下即可。

  1. 非严格次小生成树：所有生成树按照边权和从小到大排序排名第二的生成树的边权和。

解法：我们很容易发现这样一件事情，非严格最小生成树只可能和最小生成树差一条边。为什么？如果我们换一条边，可以看成加入一条新边，然后树上多了一个环，删除一条旧边。新边边权记为 \(x\)，旧边记为 \(y\)。由于这已经是最小生成树了，所以我们换完边权肯定不会变小，这样就有 \(x\ge y\)，边权差就变成了 \((x-y)\)，它非负。换两次肯定不会比换一次小，所以我们换一次。从而我们也容易得到我们要让 \(y\) 尽量大。所以我们可以求出来最小生成树，每次试着加入一条边 \((u, v, w)\)。维护 \(u\) 到 \(v\) 中最大的边权再试着换掉。树上路径最值，倍增一下即可。

  1. 严格次小生成树：就是边权严格大于最小生成树的边权和最小的生成树。这个绕口令大家可以多读几遍（不是

解法：仿照非严格次小生成树的操作，我们会发现它和最小生成树顶多之差一条边，但是我们这次就不一样了。新边记为 \(x\)，旧边记为 \(y\)，我们这次严格要求 \(x>y\)。首先 \(x\ge y\) 是肯定满足的，所以我们还可以记录 \(u, v\) 之间最大的边。但是如果它和 \(x\) 相等怎么办？所以还可能换严格次大的边，我们要记录这个东西。

怎么求树上路径边权次大的边？树上倍增。这里面倍增有点点小细节。我们令 \(jump(i, j)\) 为 \(i\) 的 \(2^j\) 级祖先，\(f(i, j)\) 为 \(i\) 到它 \(2^j\) 级祖先的最大边权，\(g(i, j)\) 为 \(i\) 到它 \(2^j\) 级祖先的次大边权。\(f(i, j) = \max\{f(i, j - 1), f(jump(i, j - 1), j - 1)\}\) 这是不必说的。那么 \(g\) 呢？\(i\) 到 \(2^j\) 级祖先有两段——\(i\) 到 \(jump(i, j - 1)\)；\(jump(i, j - 1)\) 到 \(jump(i, j)\)。不难发现当

  • \(f(i, j - 1) = f(jump(i, j - 1), j - 1)\) 时，\(g(i, j) = \max\{g(i, j - 1), g(jump(i, j - 1), j - 1)\}\)。
  • \(f(i, j - 1) > f(jump(i, j - 1), j - 1)\) 时，\(g(i, j) = \max\{g(i, j - 1), f(jump(i, j - 1), j - 1)\}\)。
  • \(f(i, j - 1) < f(jump(i, j - 1), j - 1)\) 时，\(g(i, j) = \max\{f(i, j - 1), g(jump(i, j - 1), j - 1)\}\)。

还是蛮好理解的吧，下面我们来看看几道题 qwq

Kruskal 重构树

Kruskal 重构树很厉害，比上面说的东西都要厉害，所以要把它单独拿出来。

还记得 Kruskal 的本质吗？

起初是 \(n\) 个互不干涉的点，中间每个局面都是一个森林（初始盘面的 \(n\) 个孤立的点其实也不是不能看成森林），每次都可以选一条边，连接两棵树，最后变成一棵树。

Kruskal 重构树就是，每次选一条边的时候，建立一个虚点进行连接，点权为边权，然后将两个连通块连向这个点。这样说比较抽象，举个例子就很容易懂了，比如酱紫
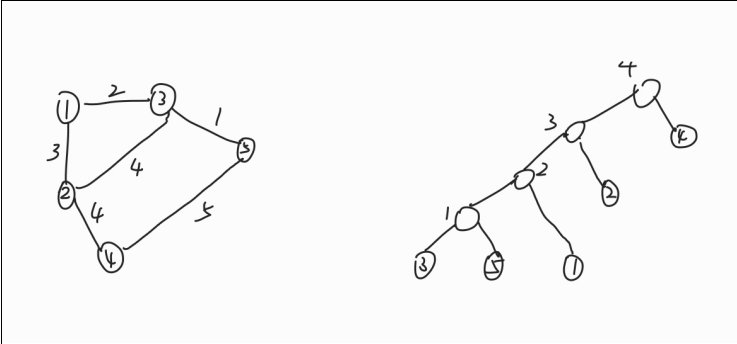
pPk7nCF.png
（这张图是从 Democy 巨爷的讲义上偷的 QWQ）

那么有了 Kruskal 重构树，它有什么性质呢？

  1. 原图中的所有点在其中都是叶子节点。
  2. 如果把叶子节点点权看成 \(-inf\) 的话，点权满足大根堆性质。而且从上到下点权单调不升。
    为什么？因为每次一定是深层的树我们先合并，用的边权小，后合并的边权大。
  3. 对于 \(u, v\) 的瓶颈路，它们 LCA 的点权就是它最小瓶颈路上最长边的长度。
    为什么？我们不妨先建出来最小生成树。Kruskal 过程就是从小到大加入所有边，当 \((u, v)\) 第一次连通时，由于是从小到大加入边的，所以这条边就是最长边。对应到 Kruskal 重构树上去，每次就是合并两个连通块（虽然过程中多了一个建立虚点）。连接 \(u, v\) 所对应的连通块，连通块里面的点互相间的最长边也就出来了，是这个边权 \(w\)。对应到图上，就是他们的 LCA。

一些题目

P4047

典题。当我们看见了“最小距离最长”，是不是和瓶颈树有点像？虽然这道题很明显不是瓶颈树，但是我们可以用一点相似的想法。

我们很容易发现这样一件事情：最近的两个点一定在同一个部落里面。为什么？如果不在同一个集合里面，那么我们的最近距离只会变短，但不会变长。所以我们可以采用 Kruskal 的方法不断加入边，直到有 \(k\) 个连通块时停止，这个时候就已经划分好了所有部落了，直接统计即可。这就是很贪心的思路。

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e3;
int n, k;
double x[MAXN + 10], y[MAXN + 10];
struct node {
	int from, to;
	double val;
} edge[MAXN * MAXN + 10];
bool cmp(node &x, node &y) {
	return x.val < y.val;
}
double dist(int i, int j) {
	return sqrt((x[i] - x[j]) * (x[i] - x[j]) + (y[i] - y[j]) * (y[i] - y[j]));
}

int fa[MAXN + 10];
int Find(int x) {
	if(fa[x] == x) return x;
	else return fa[x] = Find(fa[x]);
}
void Union(int u, int v) {
	int U = Find(u), V = Find(v);
	fa[U] = V;
}

void init() {
	cin >> n >> k;
	for(int p = 1; p <= n; p++)
		fa[p] = p;
	for(int p = 1; p <= n; p++)
		cin >> x[p] >> y[p];

	int tot = 0;
	for(int p = 1; p <= n; p++) {
		for(int i = 1; i <= n; i++) {
			edge[++tot].from = p;
			edge[tot].to = i;
			edge[tot].val = dist(p, i);
		}
	}

	sort(edge + 1, edge + tot + 1, cmp);
	int cnt = n;
	for(int p = 1; p <= tot; p++) {
		int u = edge[p].from, v = edge[p].to;
		if(Find(u) != Find(v))
			Union(u, v), cnt--;
		if(cnt == k) break;
	}
	double ans = 0x3f3f3f3f;
	for(int p = 1; p <= tot; p++) {
		int u = edge[p].from, v = edge[p].to;
		if(Find(u) != Find(v))
			ans = min(ans, edge[p].val);
	}
	cout << fixed << setprecision(2) << ans << endl;
}
int main() {
	init();
}

UVA1395

我们不难想到这种暴力做法，按边权从小到大排序，对于每条边 \(i\)，不断向右加入边 \(j\)（当然如果在同一个连通块就不加入了，和 Kruskal 一样），直到构成一棵生成树，这样的生成树一定是含边 \(i\) 中最苗条的。怎么证明？我们每次求苗条生成树实际上就是求从边权大于等于第 \(i\) 条边的边（包括第 \(i\) 条边）的最小瓶颈树，那么我们的过程和 Kruskal 一样也就不难理解了 awa

顺便这道题本来我以为边数差不多 \(1e4\) 那么 \(O(m^2\log_2 n)\) 就很危险，不过实际上 \(m\le \dfrac{100\times 99}{2} = 4950\)。这里面有一个除以二还是很灵性的……

//SIXIANG
#include <iostream>
#include <algorithm>
#include <vector>
#define KILLERQUEEN 2147483647//I like this song(
#define MAXN 100000
#define QWQ cout << "QWQ" << endl;
using namespace std;
struct node {
	int from, to, val;
};
int fa[1010], n, m;
node edge[50 * 100 + 10];
bool cmp(node &x, node &y) {
	return x.val < y.val;
}
int Find(int x) {
	if(fa[x] == x) return x;
	else return fa[x] = Find(fa[x]);
}
void Union(int u, int v) {
	int U = Find(u), V = Find(v);
	fa[V] = U;
}
int init() {
	cin >> n >> m;
	if(!(n + m)) return -1;
	
	for(int p = 1; p <= n; p++) fa[p] = p;
	for(int p = 1; p <= m; p++)
		cin >> edge[p].from >> edge[p].to >> edge[p].val;
	
	sort(edge + 1, edge + m + 1, cmp);
	
	int L = 1, R = 1, ans = KILLERQUEEN;
	for(; L <= m; L++) {
		int cnt = 0;
		for(int p = 1; p <= n; p++) fa[p] = p;
		for(R = L; R <= m; R++) {
			if(Find(edge[R].from) != Find(edge[R].to)) {
				Union(edge[R].from, edge[R].to);
				cnt++;
			}
			if(cnt == n - 1)
				ans = min(ans, edge[R].val - edge[L].val);
		}
	}
	cout << (ans == KILLERQUEEN ? (-1) : ans) << endl;
	return 0;
}
int main() {
	while(1)
		if(init() < 0) return 0;
}

CF1851G

一道很巧妙地题目。我们不难发现这样一点，\((u, v)\) 两点之间的耗费可以看成一个边权 \((h_i - h_j)\)，此时问题转化成了给出 \(q\) 组询问，每次问你从 \(s\) 到 \(t\) 有没有一条路径长度小于等于 \(e\)。很显然这个东西根本不可做。然后我们深入思考，这道题没有直接给出边权，而是用一个 \(h\) 来给出的，那么这样有什么性质呢？稍加思索即可得出，如果从 \(s\) 走到了点 \(p\)，那么花费一定是 \(e+h_s-h_p\)。\(e, h_s\) 已知。

这题并不让我们求最短路径，而是有没有这样的路径，所以问题就变成了这个——有没有一条从 \(s\) 到 \(t\) 的路径，满足其中所有经过的点 \(p\) 都有 \(h_p\le e+h_s\)。如果只有一组询问，我们很容易得到解法：把所有点权小于等于 \(e+h_s\) 的点加入图里面，然后判断 \(s, t\) 的连通性，可以用并查集。如果多组询问呢？我们可以把所有询问离线一下，按照 \(e+h_s\) 排序，这样可以保证所有点只增不删，把边也排序一下，对于边 \((u, v)\) 按照 \(\max{h_u, h_v}\) 排序（因为只有 \(h_u \le e + h_s, h_v \le e + h_s\) 同时满足才会加入图里面），用双指针一个扫询问，一个加入边，最后并查集判连通即可。

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2e5;
int n, m, h[MAXN + 10];
struct node {
	int from, to, val;
} edge[MAXN + 10];
vector <node> gra[MAXN + 10];
bool cmp1(node &x, node &y) {
	return x.val < y.val;
}

struct query {
	int s, e, t, ind;
} Q[MAXN + 10];
bool cmp2(query &x, query &y) {
	return (x.e + h[x.s]) < (y.e + h[y.s]);
}
int ANS[MAXN + 10];

int fa[MAXN + 10];
int Find(int x) {
	if(fa[x] == x) return x;
	else return fa[x] = Find(fa[x]);
}
void Union(int u, int v) {
	int U = Find(u), V = Find(v);
	fa[U] = V;
}

void init() {
	cin >> n >> m;
	for(int p = 1; p <= n; p++)
		fa[p] = p;
	for(int p = 1; p <= n; p++)
		cin >> h[p];

	for(int p = 1, x, y, z; p <= m; p++) {
		cin >> x >> y;
		edge[p].from = x;
		edge[p].to = y;
		edge[p].val = max(h[y], h[x]);
	}

	sort(edge + 1, edge + m + 1, cmp1);
	int q; cin >> q;
	for(int p = 1; p <= q; p++) {
		cin >> Q[p].s >> Q[p].t >> Q[p].e;
		Q[p].ind = p;
	}
	sort(Q + 1, Q + q + 1, cmp2);

	int j = 1;
	for(int i = 1; i <= q; i++) {
		int limit = h[Q[i].s] + Q[i].e;
		while(j <= m)
			if(edge[j].val <= limit)
				Union(edge[j].from, edge[j].to), j++;
			else break;
		ANS[Q[i].ind] = (Find(Q[i].s) == Find(Q[i].t));
	}
	for(int p = 1; p <= q; p++)
		cout << (ANS[p] ? "YES" : "NO") << endl;
	cout << endl;
}
int main() {
	int T; cin >> T;
	while(T--)
		init();
}

这可能是一种比较典的离线做法，那么它可不可以在线呢？有的，就是这道喜闻乐见（雾）的题目

P4768

这道题就是美名远扬的 SPFA 死了梗的来源地，但是这不是重点（

我们来看看这道题，和上面那道题很像。我们抽象一下题目

给定一张 \(n\) 点 \(m\) 条边的图，每条边有两个属性——边权和海拔。给出 \(q\) 组询问，给出一个出发点 \(s\) 和水位线 \(e\)。如果一条边海拔不低于水位线那么就可以通过，求从 \(s\) 出发能走到哪个点 \(t\)，使得 \(t\) 到 \(1\) 最短路最小。

一个比较显然的事情就是我们可以用 Dijkstra（但是不能用 SPFA 因为这道题额外卡了）预处理从 \(1\) 点开始到每个点的最短路记为 \(dis(i)\)。然后我们的问题就转化成了，每次询问一个 \(s\) 和 \(e\)，每次经过的边要求海拔大于等于 \(e\)，求能到的 \(dis(t)\) 最小的 \(t\)。

如何处理每次经过的边要求海拔大于等于 \(t\) 呢？我可以向上面一道题一样离线，但是这题要求我们强制在线，我们不能离线。我们可以怎么办？回到原题上来，我们要干的事情就是，找到经过的边海拔大于等于 \(e\) 的，能到的最小的 \(t\)。其实就是问你 \(s\) 到 \(t\) 最短边是不是大于等于 \(e\)。这看上去和我们的瓶颈路很像，类似的证明方法求一个最大生成树，最大生成树上 \(s, t\) 两点之间求一个最短边即可。但是这里是让我们求所有点，怎么办？我们用 Kruskal 重构树。这里是最大生成树所以此时重构树点权满足大根堆性质。然后结合一下 Kruskal 重构树我们容易得到对于点 \(u\)，它所有子树中的节点互相间的最短边一定大于等于 \(val_u\)（\(val_u\) 是 \(u\) 的点权）。

维护一下 \(s\) 点的祖先 \(anc\) 满足 \(val_{anc}> e\) 且 \(val_{anc}\) 最小。怎么维护？树上倍增。

#include <bits/stdc++.h>
#define QWQ cout << "qwq" << endl;
using namespace std;
const int N = 6e5, M = 4e5, inf = 0x3f3f3f3f;
struct E {
	int from, to, val, hight;
} edge[M + 10];
bool cmp(E &x, E &y) {
	return x.hight > y.hight;
}
struct node {
	int to, val;
	node(int T, int V) {
		to = T, val = V;
	}
	bool operator < (const node &other) const {
		return val > other.val;
	}
};

int n, m;
int fa[N + 10], root[N + 10], RT;
struct tree {
	int ls, rs, val;
} T[4 * N + 10];
int Find(int x) {
	if(x == fa[x]) return x;
	else return fa[x] = Find(fa[x]);
}
void Union(int u, int v) {
	int U = Find(u), V = Find(v);
	fa[U] = V;
}
void build() {
	sort(edge + 1, edge + m + 1, cmp);
	for(int p = 1; p <= n; p++) {
		fa[p] = root[p] = p;
		T[p].val = inf;
		T[p].ls = T[p].rs = 0;
	}
	int nd = n;
	for(int p = 1; p <= m; p++) {
		int u = edge[p].from, v = edge[p].to, w = edge[p].hight;
		int U = Find(u), V = Find(v);
		if(U == V) continue;
		nd++;
		T[nd].ls = root[U];
		T[nd].rs = root[V];
		T[nd].val = w;
		root[U] = root[V] = nd;
		Union(u, v);
	} 
	RT = nd;
}

vector <node> gra[N + 10];
void link(int x, int y, int z) {
	gra[x].push_back(node(y, z));
	gra[y].push_back(node(x, z));
}
int dis[N + 10];
bool vis[N + 10];
void dijkstra() {
	memset(vis, 0, sizeof(vis));
	memset(dis, 0x3f, sizeof(dis));
	dis[1] = 0;
	priority_queue <node> que;
	que.push(node(1, 0));
	while(!que.empty()) {
		node fr = que.top(); que.pop();
		int u = fr.to;
		if(vis[u]) continue;
		vis[u] = 1;
		
		for(int p = 0; p < gra[u].size(); p++) {
			int v = gra[u][p].to, w = gra[u][p].val;
			if(dis[v] > dis[u] + w) {
				dis[v] = dis[u] + w;
				if(!vis[v]) que.push(node(v, dis[v]));
			}
		}
	}
}

int jump[N + 10][30], value[N + 10];
void dfs(int u, int fa) {
	value[u] = dis[u];
	
	jump[u][0] = fa;
	for(int p = 1; p <= 20; p++)
		jump[u][p] = jump[jump[u][p - 1]][p - 1];
	if(T[u].ls) dfs(T[u].ls, u);
	value[u] = min(value[u], value[T[u].ls]);
	if(T[u].rs) dfs(T[u].rs, u);
	value[u] = min(value[u], value[T[u].rs]);
}
int query(int s, int e) {
	//Find t(T[t].val >= e and T[t].val smallest)
	
	int t = s;
	for(int p = 20; p >= 0; p--)
		if(T[jump[t][p]].val > e)
			t = jump[t][p];
	return value[t];
}
void clear() {
	for(int p = 0; p <= N; p++)
		gra[p].clear();
	memset(jump, 0, sizeof(jump));
}
void init() {
	clear();
	cin >> n >> m;
	for(int p = 1; p <= m; p++) {
		cin >> edge[p].from >> edge[p].to >> edge[p].val >> edge[p].hight;
		link(edge[p].from, edge[p].to, edge[p].val);
	}
	build();
	dijkstra();
	memset(value, 0x3f, sizeof(value));
	dfs(RT, 0);
	int Q, K, S, last = 0;
	cin >> Q >> K >> S;
	while(Q--) {
		int s, e;
		cin >> s >> e;
		s = (s + K * last - 1) % n + 1;
		e = (e + K * last) % (S + 1);
		cout << (last = query(s, e)) << endl;
	}
}
int main() {
	int T; cin >> T;
	while(T--)
		init();
}

P2573

有向图的最小生成树？——朱刘算法！

我当然不会朱刘算法，而且省选并不会给你放一道黑科技板子，所以我们要深入研究题目性质。注意到这里面有一个海拔，而且是在点数最大的前提下走的路最少。

我们先看第一问点数最大，这简单我 dfs 一下就好了吧。

然后我们看第二问，最小有向生成树。直接解肯定不好做，但是我们是在点数最大的前提下，这给了我们启发。首先我们会发现定向这个玩意好像我可以用 Prim，当然我可以用 Prim 的框架跑。可是直接 Prim 是错的，举个小栗子，\(n = 3, m = 3\) 的图中，\(h(1) = 3, h(2) = 2, h(3) = 1\)，然后有边 \((1, 2, 1), (1, 3, 2), (3, 2, 1)\)。Prim 会先选 \((1, 2, 1)\) 这条边，但事实上我们应该先选 \((1, 3, 2)\)，否则我们就没办法做到点数最大了。怎么办？我们 Prim 的时候按照海拔从大到小排序就好了。

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2e5;
#define int long long
int h[MAXN + 10], inf, dis[MAXN + 10];
bool vis[MAXN + 10];
int cnt1 = 0, n, m;
struct node {
	int to, hight, val;
	bool operator < (const node &other) const {
		if(hight != other.hight) return hight < other.hight;
		else return val > other.val;
	}
	node(int T, int H, int V) {
		to = T, hight = H, val = V;
	}
};
vector <node> gra[MAXN + 10];
void link(int x, int y, int z) {
	gra[x].push_back(node(y, h[y], z));
}
bool has[MAXN + 10];
void dfs(int u) {
	has[u] = 1, cnt1++;
	for(int p = 0; p < gra[u].size(); p++) {
		int v = gra[u][p].to;
		if(!has[v]) dfs(v);
	}
}

void Prim() {
	int ans = 0;
	memset(dis, 0x3f, sizeof(dis));
	dis[1] = 0;
	priority_queue <node> que;
	que.push(node(1, h[1], 0));
	while(!que.empty()) {
		node fr = que.top(); que.pop();
		int u = fr.to;
		if(vis[u]) continue;
		vis[u] = 1;
		ans += fr.val;

		for(int p = 0; p < gra[u].size(); p++) {
			int v = gra[u][p].to, w = gra[u][p].val;
			if(dis[v] > w) {
				dis[v] = w;
				if(!vis[v]) que.push(node(v, h[v], dis[v]));
			}
		}
	}
	cout << ans << endl;
}

void init() {
	cin >> n >> m;
	for(int p = 1; p <= n; p++) cin >> h[p];
	for(int p = 1, x, y, z; p <= m; p++) {
		cin >> x >> y >> z;
		if(h[x] >= h[y]) link(x, y, z);
		if(h[y] >= h[x]) link(y, x, z);
	}
	dfs(1);
	cout << cnt1 << ' ';
	Prim();
}
signed main() {
	init();
}

顺带一提，为啥我跑得这么慢呜哇，虽然我有 define int long long 这样的坏习惯，但是为啥别人会比我快 1s 啊呜呜呜，实在是人傻常数大，嘲讽。

P4180

做法上面扯完了。这道题是我第一次在 lyd 巨佬的书上看到的，当时应该是照着书的做法剽的代码，所以代码写的不伦不类我是真的看不懂，我明天重写一份吧 qwq

标签：10,val,int,MST,最小,生成,edge,题单
From： https://www.cnblogs.com/thirty-two/p/17606673.html

相关文章

  • 第二周训练题单
    R、paritygame#include<bits/stdc++.h>usingnamespacestd;#defineintlonglongconstintN=1e5+50;intn,m,fa[N],r[N];map<int,int>mp;intans,cnt=0;intfind(intx){if(fa[x]==-1)returnx;intpre=find(fa[x])......
  • 教程：开始使用 Microsoft Sentinel 中的 Jupyter Notebook 和 MSTICPy——威胁狩猎用，含
    教程：开始使用MicrosoftSentinel中的JupyterNotebook和MSTICPy项目2022/05/026个参与者  备注AzureSentinel现在称为MicrosoftSentinel，我们将在几周内更新相关页面。详细了解最近的Microsoft安全性增强。本教程介绍如何运行“MicrosoftSentinelMLNotebook入门......
  • [并查集] 题单刷题摘要
    题单1.P6121[USACO16OPEN]ClosingtheFarmGP3144[USACO16OPEN]ClosingtheFarmS（逊版）思路\(\scr{Solution}\)每一时刻关闭农场，求是否全联通。也就是维护将单个集合分成多个集合。很容易想到爆搜算法，用vector邻接表建图，每次跑完图就将当前点的连边关系删去。复杂度......
  • 第三周训练题单
    数字三角形#include<bits/stdc++.h>usingnamespacestd;#defineintlonglongint32_tmain(){ios::sync_with_stdio(false),cin.tie(nullptr);intn;while(cin>>n){for(inti=1;i<=n;i++){for(in......
  • 第三周题单
    互不侵犯KING思路：dp[i][j][k]表示前i行，且已经用了j个国王，且第i行的摆放状态为k（二进制）；dp[i][j][k]=dp[i-1][j-num[now]][pre]，now表示第i行的状态，pre表示上一行的状态，num[i]维护一行的状态为i的国王数量，且需保证now和pre满足为相邻行的条件#include<bits/stdc++.h>usingname......
  • 贪心（不同情况下有不同策略）题单报告
    书接上回。感觉这个标题起得云里雾里的颇有上次讲的“反悔自动机”的奇妙风范，坏了会回旋镖插我自己身上了（感觉这样的贪心很厉害。什么叫不同情况下有不同策略呢？就是说你要分讨，分讨的每一种情况我们都要保证这是当前的最优解。这听起来是不是还是很扯，其实这是为了方便我自己看的......
  • 贪心（反悔贪心）题单报告
    Democy爷给了一份贪心的题单，但是由于我是小笨比，所以很多题我都不是很会做，现在来简单写一份总结，加强一下印象qwq。首先什么叫贪心？贪心就是我每次都选择一个最大值。比如说我现在有\(n\)个物品，每个物品都有一个价值，我们可以选\(k\)件物品，我们怎么样让选择的价值和最大呢？傻子......
  • 第二周训练题单
    多项式输出小细节比较多#include<bits/stdc++.h>usingnamespacestd;#defineintlonglongint32_tmain(){ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);intn;cin>>n;for(intx,i=n;i>=0;i--){......
  • Linux系列---【CentOS 7通过MSTSC连接远程桌面】
    安装对应的yum源yumlistlightdmxorgxrdpxrdp可以看到这些软件都在epel中，如果没有的话，请先安装对应的yum源。命令如下：yuminstall-yepel-release确认yum源没有问题之后，我们就可以进行安装了。安装lightdmxorgxrdpxrdplightdm提供了图形登录界面和用户会话管理......
  • ubuntu云服务器通过mstsc远程登录
    安装一个轻量级桌面环境，并实现通过Windows11的远程桌面服务访问，以及将所需的服务添加到开机自启，可以按照以下步骤进行操作：首先，通过SSH登录到云服务器。可以使用终端或PuTTY（Windows用户）等工具进行SSH登录。安装轻量级桌面环境，推荐使用Xfce桌面环境。运行以下命令......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99