前言
数学符号约定
\(\operatorname{lowbit}(x)\):表示 \(x\) 的二进制最低位。
\([a,b]\):表示区间 \(a\sim b\),其中包含 \(a,\,b\) 端点,其区间长度为 \(b - a + 1\)。
如非特殊说明,将会按照上述约定书写符号。
题目大意
有一个初始全为 \(0\) 的序列 \(A\),你需要支持一下操作:
add P F:将 \(a_P\) 增加 \(F\)。
find L R:查询区间 \([L,R]\) 的和。
题目分析
树状数组板子题,因为是模板题,所以在这里介绍一下树状数组。
很多时候,大家习惯性的把树状数组放在线段树前面讲,然而我认为把线段树放在树状数组前面讲更够更方便大家理解树状数组这个数据结构。
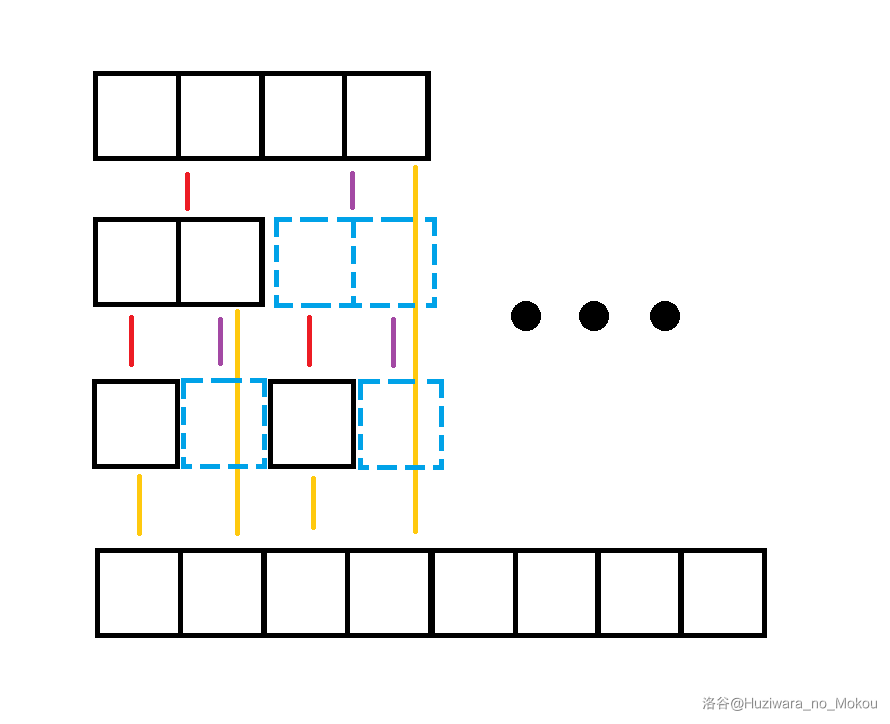
如果你熟悉线段树的话,看到上图应该就能立刻理解树状数组是个什么东西了,它本质上就是一颗没有右儿子的线段树。
我们首先考虑建立一棵树,让叶子节点维护原始信息,非叶子节点维护区间信息。然后我们让这棵树成为一颗二叉树,因为这样的复杂度可以跟二分一样挂钩。然后让一个节点左儿子维护的是区间 \([L,mid]\),让右儿子维护 \([mid+1,R]\),这样一颗二叉树就是我们所说的线段树,它的建树是 \(O(n)\) 的,单点修改和区间查询都是 \(O(\log n)\) 的。
但是,让我们考虑一下,我们真的需要把整棵线段树全部建出来吗?答案是否定的,在本题中,像这种「单点加、维护区间和」问题,我们可以偷个懒,我们把线段树的右儿子全部砍掉,然后考虑此时我们的单点修改,其实就可以直接对该点所在的区间进行增量变化。
这么说可能比较抽象,我们来一起举个例子:现在,我们需要修改 \(a_4\) 这个位置,如果是线段树的话,我们就需要递归到维护 \(a_4\) 的叶子节点,增加完后在一步一步的 pushup 上去,但是这样太麻烦了,我们换一个思路,我们修改的时候从离 \(4\) 最近的左儿子——区间 \(1 \sim 4\) 开始改,然后一步一步往上跳直到跳到根节点,边跳边改,这样就没有我们递归下去的那一部分常数了。
但是,我们的任何创新都要建立在正确的基础上,我们先反问一下自己,这样能保证正确性吗?如果你要是还像线段树那样区间查询的话,那确实是不能保证正确性的。因为毕竟我们砍掉了右儿子嘛,我们递归到的区间拼起来肯定是不完整的。不过,让我们换个思路,考虑转换一下区间和,不难想到,区间和还等于两个前缀和的差。所以如果我们能够保证查询前缀和的结果是正确的就好了。
幸运的是,我们可以保证查询前缀和的正确性,我们考虑我们离某数 \(x\) 最近的左儿子所维护的区间右端点,实际上就是数 \(x\) 本身,那么前缀和一定保证需要加上 \(x\) 及其之前的部分,所以此时我们可以保证查询的前缀和一定是完整的。其实,上面内容所讲的数据结构,就是现在我们要讲的「树状数组」。
好,原理讲完了,现在该谈谈如何写代码,因为我们将 \(a_x\) 的信息放到了离 \(x\) 最近的左儿子里面,然后它还是那个左儿子所维护的区间的右端点,所以我们不妨直接让我们的数组 \(B\) 的第 \(x\) 位置维护那个左儿子所维护的区间。然后我们现在对编号进行一下分析,不难发现,我们的父亲节点一定在 \(x + \operatorname{lowbit}(x)\) 里面。证明比较复杂,不过理由如下:
首先,我们肯定有如下引理:
\(\text{Lemma 1}\):若当前点 \(x\) 表示的区间长度为 \(len\),那么它的父区间所代表的节点位置一定是 \(x + len\)。
\(\text{Proof}\):考虑我们子区间的定义是来自于向下分治的结果,所以子区间的长度一定是父区间的一半,由于我们砍掉了分治的右向分支,并用右端点 \(a\) 的位置保存最长的右端点为 \(a\) 的区间信息,所以不难得出,当我们 $x $ 增加 \(len\) 的时候就跳到了区间的右端点,也就是 \(x\) 所代表区间的父区间。
所以,我们现在所需要证明的就变成了 \(\operatorname{lowbit}(x)\) 为 \(x\) 所代表的区间。
首先,我们不难得出一个引理:
\(\text{Lemma 2}\):对于编号为 \(2^n\) 的位置,其一定代表了区间 \([1,2^n]\)。
\(\text{Proof}\):首先,我们让位置 \(1\) 只维护单点 \(1\) 的信息,然后根据 \(\text{Lemma 1}\),我们不难得出其父区间位置为 \(2\),其父区间的父区间位置为 \(4\),以此类推,其第 \(n\) 级父区间位置一定为 \(2^n\),由于我们是从 \(1\) 一路推上来的,又由于位置 \(a\) 所维护的是最长的右端点为 \(a\) 的区间信息,故可以得出 \(\text{Lemma 2}\)。
其次,我们还有一个引理:
\(\text{Lemma 3}\):树状数组为一个分形结构。
\(\text{Proof}\):显然,因为树状数组是反向分治的结果,所以对于任意一对左右儿子,我们都有左儿子的结构与右儿子的一样。
那么对于一个数 \(x\),我们可以根据 \(\text{Lemma 3}\) 来得到一个新的引理:
\(\text{Lemma 4}\):位置 \(x\) 总是可以被分形直到所维护的相对区间为 \([1,2^n]\)。
\(\text{Proof}\):首先,我们总能将任意正整数分解为若干个 \(2^i\) 相加,于是我们不妨设 \(2^m\) 为 \(x\) 的最高位,根据 \(\text{Lemma 1}\),我们可以得出 \(x\) 所在的区间一定在 \([2^m+1,2^{m+1}]\) 区间内。根据 \(\text{Lemma 3}\),由于左右儿子结构相同,我们不妨对区间重新标号,让 \(2^m+1\) 为当前区间的 \(1\) 号位置。重复上述过程,直到 \(x\) 为 \(2^n\) 次方。此时根据 \(\text{Lemma 2}\),我们不难得出 \(x\) 所维护的即为相对区间 \([1,2^n]\)。
现在,我们可以综上了:
\(\text{Lemma 5}\):位置 \(x\) 所维护的区间长度为 \(\operatorname{lowbit}(x)\)。
\(\text{Proof}\):我们重新观察 \(\text{Lemma 4}\) 的证明过程,不难发现我们每一次分形都是让右儿子的位置编号全部减去 \(2^m\),也就是减去 \(x\) 的最高位,然后最后剩下的 \(2^n\) 其实就是 \(x\) 的最低位,也就是 \(\operatorname{lowbit}(x)\),又根据 \(\text{Lemma 4}\) 可以得出,位置 \(x\) 所维护的相对区间是 \([1,\operatorname{lowbit}(x)]\),故位置 \(x\) 所维护的区间长度为 \(\operatorname{lowbit}(x)\)。
故此时,对于单点加操作 add(pos, val),我们不难写出如下代码:
void add(int pos, int val) {
for(int i = pos; i <= n; i += lowbit(i)){
c[i] += val;
}
}
查询操作 query(l,r) 就变成了:
int ask(int pos){
int ans = 0;
for(int i = pos; i; i -= lowbit(i)){
ans += c[i];
}
return c[i];
}
int query(int l, int r){
return ask(r) - ask(l-1);
}
代码实现
// clang-format off
// There is No Misaka for Codeforces. /dk
#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL
#define debug(x) cerr << #x << ": " << (x) << endl;
#define debugf(fmt, args...) fprintf(stderr, fmt, ##args)
#else
#define debug(...) void(114514);
#define debugf(...) void(1919810);
#endif
namespace FastIO // Powered By LgxTpre. <3 <3 <3
{
template <typename T = int>
inline T read() {
T s = 0, w = 1; char c = getchar();
while (!isdigit(c)) { if (c == '-') w = -1; c = getchar(); }
while (isdigit(c)) s = (s << 1) + (s << 3) + (c ^ 48), c = getchar();
return s * w;
}
template <typename T>
inline void read(T &s) {
s = 0; int w = 1; char c = getchar();
while (!isdigit(c)) { if (c == '-') w = -1; c = getchar(); }
while (isdigit(c)) s = (s << 1) + (s << 3) + (c ^ 48), c = getchar();
s = s * w;
}
template <typename T, typename... Args> inline void read(T &x, Args &...args) { read(x), read(args...); }
template <typename T>
inline void write(T x, char ch) {
if (x < 0) x = -x, putchar('-');
static char stk[25]; int top = 0;
do { stk[top++] = x % 10 + '0', x /= 10; } while (x);
while (top) putchar(stk[--top]);
putchar(ch);
return;
}
} // namespace FastIO
struct ModTools {
#define int long long
ModTools(int MODD = 1e9 + 7) : MOD(MODD) { }
void ChangeMod(int MODD) { MOD = MODD; }
inline void Madd(int &a, int b) { a = a + b >= MOD ? a + b - MOD : a + b; }
inline void Msub(int &a, int b) { a = a - b < 0 ? a - b + MOD : a - b; }
inline void Mmul(int &a, int b) { a = a * b % MOD; }
inline int add(int a, int b) { return (a + b >= MOD) ? (a + b - MOD) : (a + b); }
inline int mul(int a, int b) { return (a % MOD) * (b % MOD) % MOD; }
inline int sub(int a, int b) { return (a - b < 0) ? (a - b + MOD) : (a - b); }
template <typename... Args> inline int add(int a, int b, Args &...args) { return add(a, add(b, args...)); }
template <typename... Args> inline int mul(int a, int b, Args &...args) { return mul(a, mul(b, args...)); }
template <typename... Args> inline void Madd(int &a, int b, Args &...args) { return Madd(a, add(b, args...)); }
template <typename... Args> inline void Mmul(int &a, int b, Args &...args) { return Mmul(a, mul(b, args...)); }
inline int inv(int x) {
int A = 0, B = 0;
int d = exgcd(x, MOD, A, B);
assert(d == 1);
return sub(A, 0);
}
inline int fastpow(int base, int index) {
int ans = 1;
while (index) {
if (index & 1) ans = mul(ans, base);
base = mul(base, base);
index >>= 1;
}
return ans;
}
inline int sqr(int x) { return mul(x, x); }
private:
int exgcd(int A, int B, int &X, int &Y) {
if (B == 0) {
X = 1, Y = 0;
return A;
}
int res = exgcd(B, A % B, X, Y);
int temp = Y;
Y = X - A / B * Y;
X = temp;
return res;
}
int MOD;
#undef int
};
namespace NumberTheory {
inline int gcd(int A, int B) {
int C;
while (B) C = B, B = A % B, A = C;
return A;
}
int exgcd(int A, int B, int &X, int &Y) {
if (B == 0) {
X = 1, Y = 0;
return A;
}
int res = exgcd(B, A % B, X, Y);
int temp = Y;
Y = X - A / B * Y;
X = temp;
return res;
}
} // namespace NumberTheory
// clang-format on
namespace Larry76 {
#define int long long
using namespace FastIO;
using namespace NumberTheory;
const int MAX_SIZE = 1e6 + 10;
const int INF = 0x7f7f7f7f7f7f7f7fll;
const double eps = 1e-9;
struct pii {
int x, y;
inline bool operator < (const pii &oth) const{
if(x==oth.x)
return y < oth.y;
return x < oth.x;
}
};
ModTools mt(1e9 + 7);
inline int sqr(int x) { return x * x; }
inline int random(int l, int r) {
static mt19937_64 rnd(time(0));
uniform_int_distribution<int> dist(l,r);
return dist(rnd);
}
int fac[MAX_SIZE];
int ifac[MAX_SIZE];
void initfac(int n) {
fac[0] = 1;
for(int i=1;i<=n;i++) {
fac[i] = mt.mul(fac[i-1],i);
}
ifac[n] = mt.inv(fac[n]);
for(int i=n-1;i>=0;--i) {
ifac[i] = mt.mul(ifac[i+1], i+1);
}
}
inline int C(int n, int m) { // n choose m
return mt.mul(fac[n],ifac[m],ifac[n-m]);
}
inline int A(int m, int n) { // A_n^m
return mt.mul(fac[n],ifac[m]);
}
///////////// Start Coding //////////////
int n,q;
int tree[MAX_SIZE];
inline int lowbit(int x){
return x & (-x);
}
void add(int pos, int val){
for(int i = pos; i<=n; i+=lowbit(i)){
tree[i] += val;
}
}
int ask(int pos){
int ans = 0;
for(int i=pos;i;i-=lowbit(i)){
ans += tree[i];
}
return ans;
}
int query(int l, int r){
return ask(r) - ask(l-1);
}
int findstr() {
char c = getchar();
while (c != 'a' && c != 'f') c = getchar();
return c == 'a' ? 1 : 2;
}
void main(){
read(n,q);
while(q--){
switch(findstr()){
case 1:{
int p = read();
int f = read();
add(p,f);
break;
}
case 2:{
int l = read();
int r = read();
write(query(l,r),'\n');
break;
}
}
}
}
////////////// End Coding ///////////////
#undef int
} // namespace Larry76
int main() {
#ifdef LOCAL
time_t t1 = clock();
#endif
Larry76::main();
#ifdef LOCAL
time_t t2 = clock();
fprintf(stderr, "Used Time: %lldms.\n", t2 - t1);
#endif
return 0 ^ 0;
}