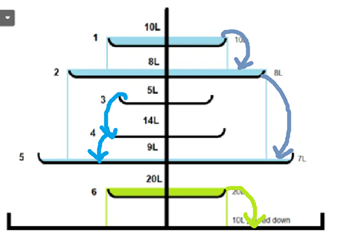
有n个盘子组成的塔,向第i个盘子上倒水,若溢出会落到下面第一个直径大的盘子里,直到落到底部的水池为止。现给出q次询问,\((r,v)\)代表向第r个盘子里倒入体积为v的水,求水最终会停在哪个盘子
一开始用ST表保存区间内盘子直径最大值,给出 \(r\) 后,递归求解 \([ r,n ]\) 区间内最大值k,并继续求 \([r,k]\) 区间内最大值,直到取到第 \(r\) 个,回溯过程中逐步计算储水量。
但是看到严格单调递增序列就放弃了
然后卡了一段时间,突然发现好像有点眼熟 (
第一个想法
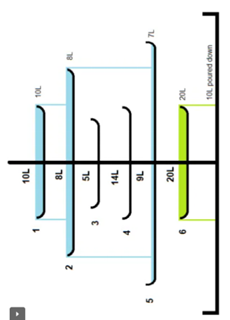
看正的比较难想,但横过来就很直观
当我们说水向下流,实际上我们在说水向右找到第一个比他大的盘子,那么就是单调栈了
数组 \(f[i]\) 表示第i个盘子下边第一个比他大的盘子编号,这样形成链状的查询,可以依次访问
但数据量太大,时间复杂度还是很高
因此要用倍增,类似ST表的方法,每次跳跃跳2的幂次
数组 \(f[i][j]\) 存储从第i个盘子开始,跳 \(2^j\) 到达的盘子编号
数组 \(summ[i][j]\) 存储从第i个盘子开始,到之上 \(2^j\) 个盘子的储水量总和
查询的时候特判当前储水量,然后从大到小循环j,向上跳跃,最后输出父节点
第二个想法 (但是没写
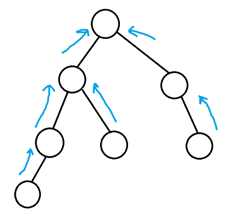
可以看到在一个大的盘子之上有许多小盘子依次连接,最终汇聚到一个统一的大盘子,又最终汇聚到底部的水池
于是这提醒我们想到树
对于一个盘子,他下面第一个直径大于它的盘子为他的父节点,上面所有可以到达他的盘子为他的子树,根节点代表底部水池
那么从叶节点向上遍历即为流水顺序,在这过程中计算储水量
但是数据太大,所以仍然要用到倍增,使用类似倍增求LCA的方法,向上寻找
但是不是求公共祖先,实质上和第一种方法相同,只不过套上了树的形式
#include <iostream>
#include <cstdio>
#include <cstring>
#include <stack>
#define ll long long
using namespace std;
const int N = 1e5 + 10;
int n, q, d[N], c[N], R, V, f[N][20], summ[N][20];
stack<int>s;
inline void Monotonic_Stack() { // 单调栈板子
for(int i = 1; i <= n; i ++) {
while (!s.empty() && d[i] > d[s.top()]) {
f[s.top()][0] = i; // 初始化右边第一个大的盘子编号
summ[s.top()][0] = c[i]; // 初始化总和
s.pop();
}
s.push(i);
}
while(!s.empty()) f[s.top()][0] = 0, s.pop();
}
inline void PrepareRMQ() { // ST表板子
for (int j = 1; (1 << j) <= n; j ++)
for (int i = 1; i <= n - (1 << j); i ++) {
f[i][j] = f[f[i][j - 1]][j - 1];
summ[i][j] = summ[i][j - 1] + summ[f[i][j - 1]][j - 1];
}
}
inline int query(int r, int val) { // 计算
if (c[r] >= val) return r;
val -= c[r]; // 先减掉当前盘子容量
for (int i = 18; i >= 0; i --)
if (f[r][i] && val > summ[r][i]) {
val -= summ[r][i]; // 向上寻找
r = f[r][i]; // 更新位置
}
return f[r][0]; // 返回父节点
}
int main() {
scanf("%d%d", &n, &q);
for (int i = 1; i <= n; i ++) scanf("%d%d", &d[i], &c[i]);
Monotonic_Stack(); // 单调栈
PrepareRMQ(); // 准备工作
while (q -- ) {
scanf("%d%d", &R, &V);
printf("%d\n", query(R, V));
}
return 0;
}