2791. 树中可以形成回文的路径数

Description

Difficulty: 困难

Related Topics: 位运算, 树, 深度优先搜索, 动态规划, 状态压缩

给你一棵 树（即，一个连通、无向且无环的图），根 节点为 0 ，由编号从 0 到 n - 1 的 n 个节点组成。这棵树用一个长度为 n 、下标从 0 开始的数组 parent 表示，其中 parent[i] 为节点 i 的父节点，由于节点 0 为根节点，所以 parent[0] == -1 。

另给你一个长度为 n 的字符串 s ，其中 s[i] 是分配给 i 和 parent[i] 之间的边的字符。s[0] 可以忽略。

找出满足 u < v ，且从 u 到 v 的路径上分配的字符可以 重新排列 形成 回文 的所有节点对 (u, v) ，并返回节点对的数目。

如果一个字符串正着读和反着读都相同，那么这个字符串就是一个 回文 。

示例 1：

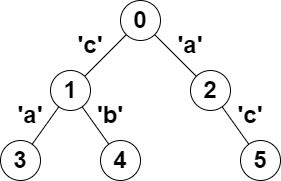
输入：parent = [-1,0,0,1,1,2], s = "acaabc"
输出：8
解释：符合题目要求的节点对分别是：
- (0,1)、(0,2)、(1,3)、(1,4) 和 (2,5) ，路径上只有一个字符，满足回文定义。
- (2,3)，路径上字符形成的字符串是 "aca" ，满足回文定义。
- (1,5)，路径上字符形成的字符串是 "cac" ，满足回文定义。
- (3,5)，路径上字符形成的字符串是 "acac" ，可以重排形成回文 "acca" 。

示例 2：

输入：parent = [-1,0,0,0,0], s = "aaaaa"
输出：10
解释：任何满足 u < v 的节点对 (u,v) 都符合题目要求。

提示：

• n == parent.length == s.length
• 1 <= n <= 10⁵
• 对于所有 i >= 1 ，0 <= parent[i] <= n - 1 均成立
• parent[0] == -1
• parent 表示一棵有效的树
• s 仅由小写英文字母组成

Solution

回文字符串等价于所有出现字符至多一个出现奇数次，可以用位运算来记录状态。
同时依据异或运算的法则，任意两个节点的异或等于从root到各个节点的状态的异或。
Language: Python3

class Solution:
    def countPalindromePaths(self, parent: List[int], s: str) -> int:
        g = defaultdict(list)

        for i, p in enumerate(parent):
            g[p].append(i)
        
        res = 0
        record = defaultdict(int)
        record[0] = 1

        def dfs(root, curr):
            nonlocal res

            for c in g[root]:
                bit = curr ^ (1 << (ord(s[c]) - ord("a")))
                res += record[bit]
                for i in range(26):
                    res += record[(1 << i) ^ bit]
                record[bit] += 1
                dfs(c, bit)

        dfs(0, 0)

        return res