题目:24. 两两交换链表中的节点
思路:
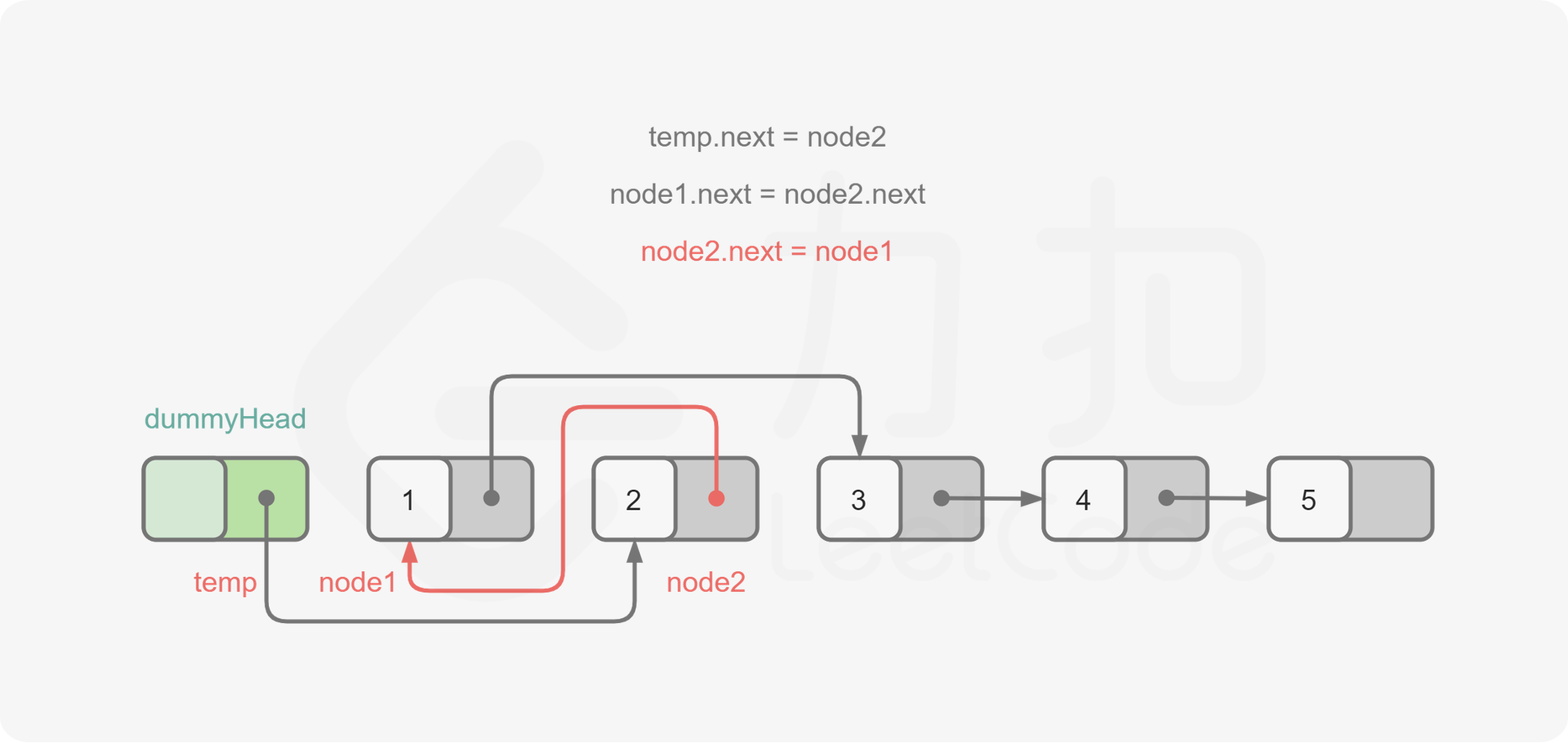
首先给他加一个虚拟头结点,然后思考反转的逻辑,这是每两个为一组,比如1,2是一组、3,4是一组,如果说1,2一组2,3一组就变成了链表的逆转了。
那么指针的逻辑是:
- 两个指针一个r指向要交换的二元组的第一个节点
- 一个l指向前一个节点
- 二元组的第二个节点直接通过
r.Next来获取t
之后切换的逻辑是:
l.Next指向tr.Next指向t.Nextt.Next指向r
然后再把这个链表"拉直",就发现交换成功了,当然要记得再迭代新的位置:
- l = r
- r = r.Next
代码:
双指针迭代
/**
* Definition for singly-linked list.
* type ListNode struct {
* Val int
* Next *ListNode
* }
*/
func swapPairs(head *ListNode) *ListNode {
// 0 1 2 开始
// 0->2,1->2.Next,2->1
res := new(ListNode)
res.Next = head // 添加虚拟头节点
l, r := res, res.Next
for r != nil {
t := r.Next
if t == nil { // 如果就剩下一个节点直接退出
break
}
l.Next = t
r.Next = t.Next
t.Next = r
l = r
r = r.Next
}
return res.Next
}
参考:
题目:19. 删除链表的倒数第 N 个结点
思路:
最简单的方式就是遍历一遍得到链表长度,然后再根据链表的长度进行操作即可。
但是题目要求一次遍历完成删除操作,那就有文章可以做了——我们可以先派遣一个先锋,让他先走n步,这样当先锋到达结尾时,后边的节点就是要删除的节点,我们整理一下:
我们需要有删除的节点的前一个节点位置的控制权
我们准备一个pre、一个cur以及tmp = cur.Next,首先让cur先走n步,然后开始一步一步遍历,if tmp== nil的时候,cur在最后一个节点的位置,pre在要删除的节点的前一个位置,此时我们只需要让pre.Next = pre.Next.Next即可完成删除操作。
迭代:直接pre和cur都下一步就可以了,即pre = pre.Next以及cur = cur.Next
代码:
/**
* Definition for singly-linked list.
* type ListNode struct {
* Val int
* Next *ListNode
* }
*/
func removeNthFromEnd(head *ListNode, n int) *ListNode {
res := new(ListNode)
res.Next = head // 虚拟头
pre, cur := res, res
for i := 1; i <= n; i++ { // 前锋先走n步
cur = cur.Next
}
for cur != nil {
tmp := cur.Next
if tmp == nil { // 此时cur在最后一个节点处,pre在要删除的元素前一个节点
pre.Next = pre.Next.Next
}
pre = pre.Next
cur = cur.Next
}
return res.Next
}
参考:
题目:面试题 02.07. 链表相交
思路:
必须要注意的一点是,这里的相交是结构上的问题,而不是数值上的问题;是真的在链表结构上有相交的部分(指向同一个地址)。
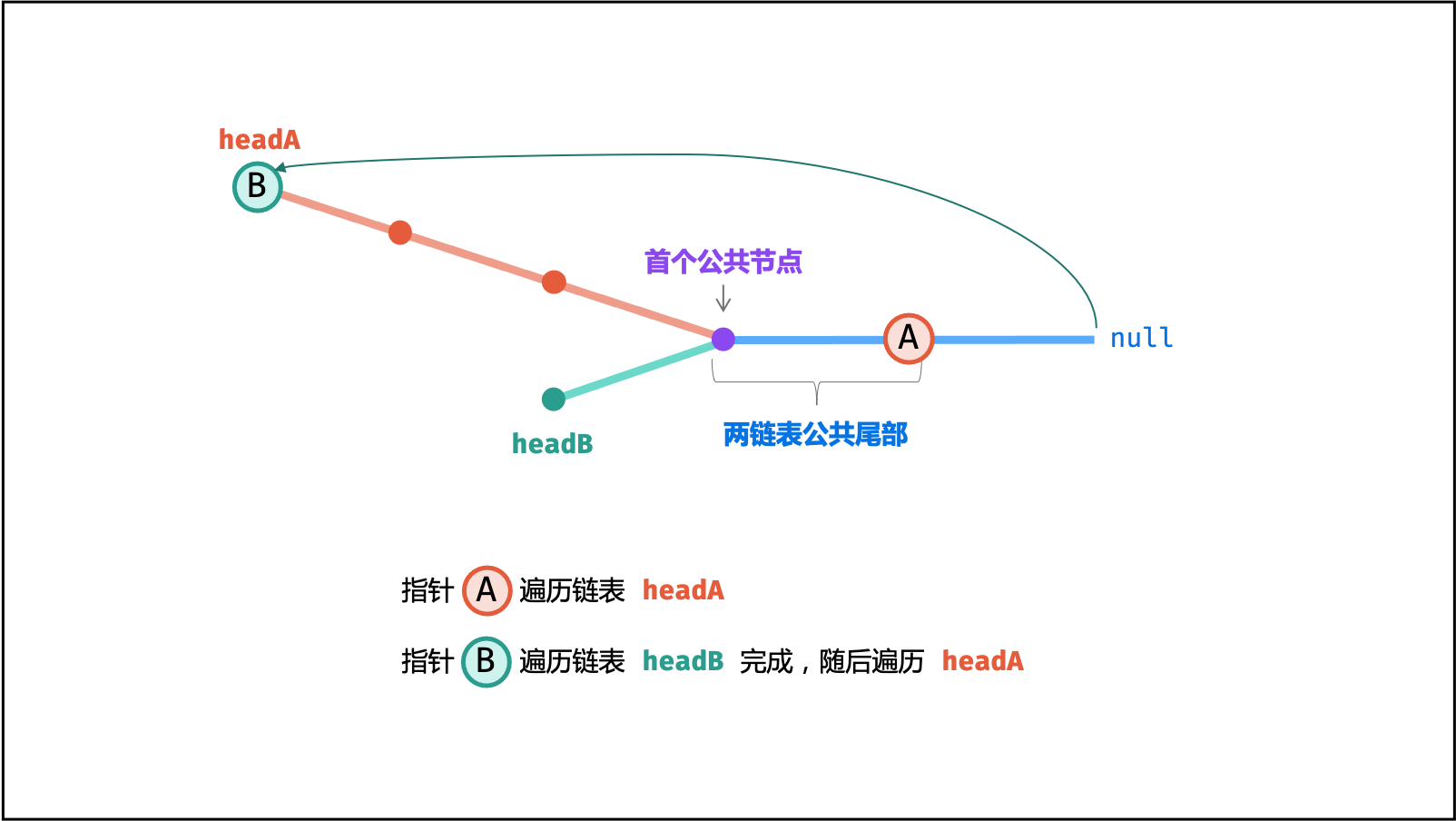
那实际上数学上的一个问题,A + B 和 B + A 同时开始走,如果有公共部分就会在最后走到一起。
当然也可以用哈希的方式来解决。
代码1:
双指针数学方法解决
func getIntersectionNode(headA, headB *ListNode) *ListNode {
nodeA, nodeB := headA, headB
for nodeA != nodeB { // 当nodeA和nodeB都是nil的时候就会停止(如果没有公共部分)
if nodeA == nil {
nodeA = headB // 跑完A跑B
}else {
nodeA = nodeA.Next
}
if nodeB == nil {
nodeB = headA // 跑完B跑A
}else {
nodeB =nodeB.Next
}
}
return nodeA // 或者nodeB
}
代码2:
哈希,空间复杂度比较高
func getIntersectionNode(headA, headB *ListNode) *ListNode {
maps := make(map[*ListNode]bool, 0)
for headA != nil {
maps[headA] = true
headA = headA.Next
}
for headB != nil {
if _, ok := maps[headB]; ok {
return headB
}
headB = headB.Next
}
return nil
}
参考:
题目:142. 环形链表 II
思路:
还是两种方法一个哈希一个双指针,这次是一个快指针一个慢指针。
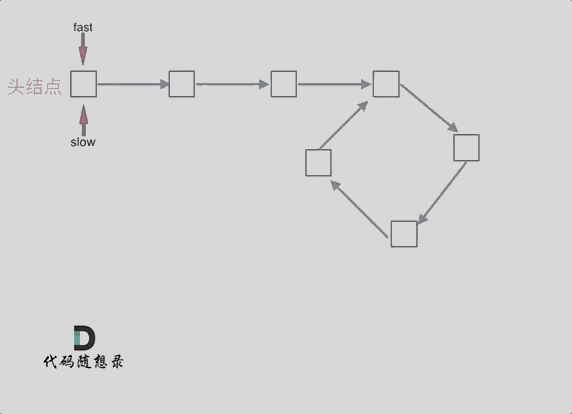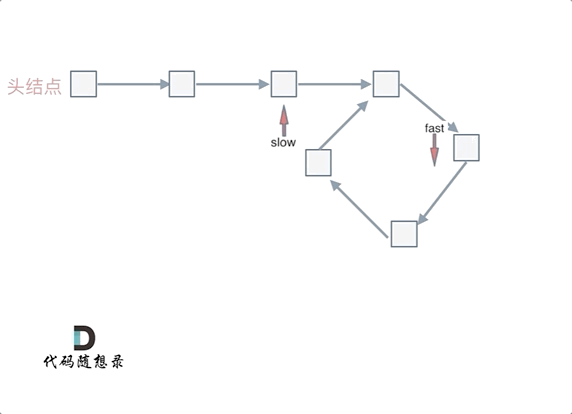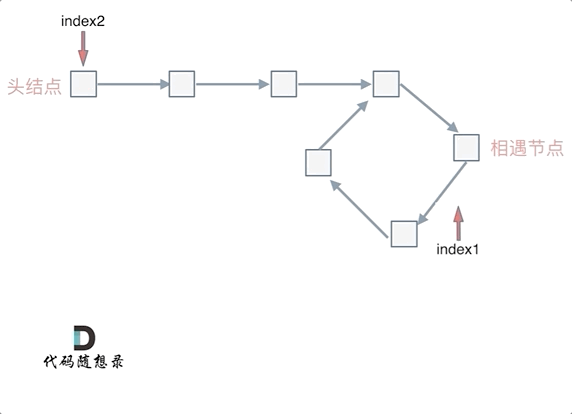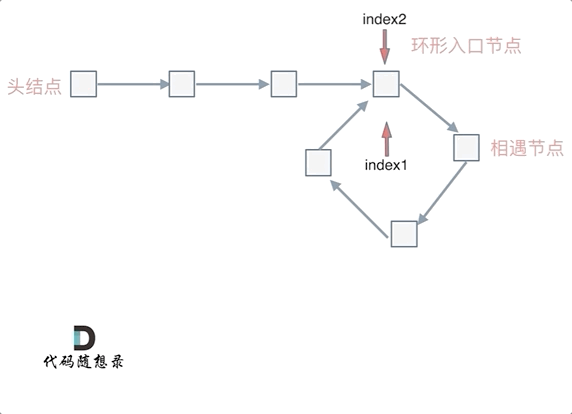
假设从头结点到环形入口节点 的节点数为x。 环形入口节点到 fast指针与slow指针相遇节点 节点数为y。 从相遇节点 再到环形入口节点节点数为 z。 如图所示:
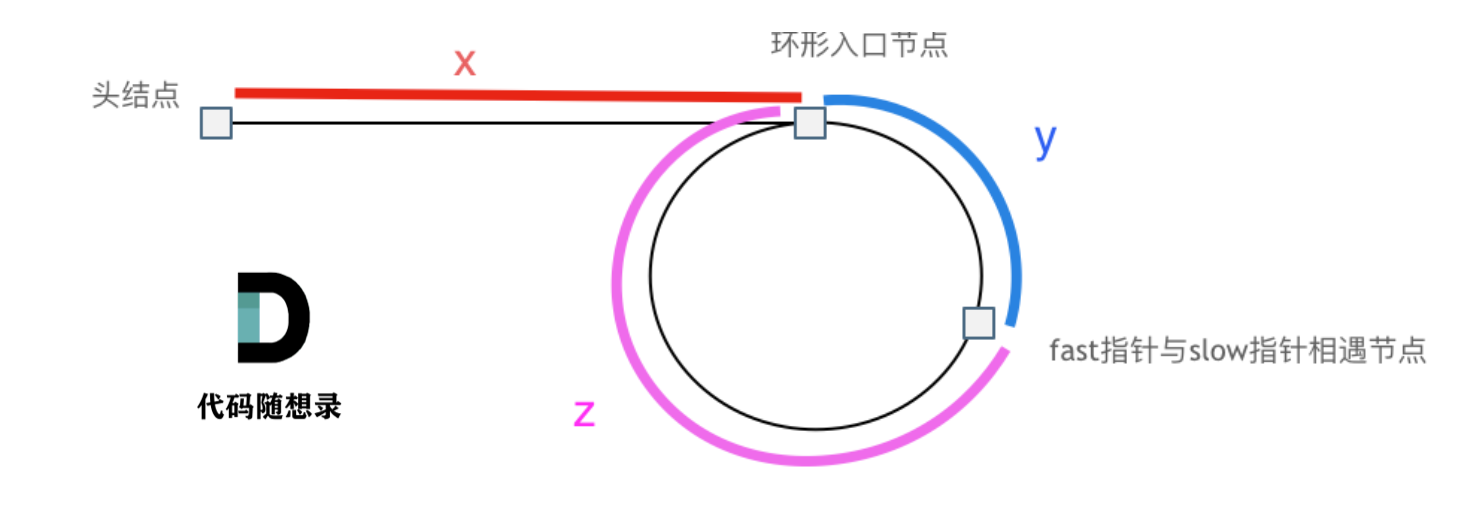
那么相遇时: slow指针走过的节点数为: x + y, fast指针走过的节点数:x + y + n (y + z),n为fast指针在环内走了n圈才遇到slow指针, (y+z)为 一圈内节点的个数A。
因为fast指针是一步走两个节点,slow指针一步走一个节点, 所以 fast指针走过的节点数 = slow指针走过的节点数 * 2:
(x + y) * 2 = x + y + n (y + z)
两边消掉一个(x+y): x + y = n (y + z)
因为要找环形的入口,那么要求的是x,因为x表示 头结点到 环形入口节点的的距离。
所以要求x ,将x单独放在左面:x = n (y + z) - y ,
再从n(y+z)中提出一个 (y+z)来,整理公式之后为如下公式:x = (n - 1) (y + z) + z 注意这里n一定是大于等于1的,因为 fast指针至少要多走一圈才能相遇slow指针。
这个公式说明什么呢?
先拿n为1的情况来举例,意味着fast指针在环形里转了一圈之后,就遇到了 slow指针了。
当 n为1的时候,公式就化解为 x = z,
这就意味着,从头结点出发一个指针,从相遇节点 也出发一个指针,这两个指针每次只走一个节点, 那么当这两个指针相遇的时候就是 环形入口的节点。
也就是在相遇节点处,定义一个指针index1,在头结点处定一个指针index2。
让index1和index2同时移动,每次移动一个节点, 那么他们相遇的地方就是 环形入口的节点。
代码:
双指针
/**
* Definition for singly-linked list.
* type ListNode struct {
* Val int
* Next *ListNode
* }
*/
func detectCycle(head *ListNode) *ListNode {
slow, fast := head, head
for fast != nil {
slow = slow.Next // 慢指针每次走一步
if fast.Next == nil {
return nil
}
fast = fast.Next.Next // 快指针每次走两步
if fast == slow { // 当快指针 = 慢指针时,满指针距离节点距离 = 头部距离节点距离
p := head
for p != slow {
p = p.Next
slow = slow.Next
}
return p // 找到入口
}
}
return nil
}
参考:
总结:
做链表题最好是有一个虚拟头指针辅助,作甚么操作都会变得方便一点,翻转不需要。
要对链表进行操作:
- 首先就是想好在一次变更中,按照什么顺序进行Next的变更才能得到正确的结果,一般可以通过画图来辅助理清思路。
- 然后根据上述过程找到对他操作会对哪些节点产生影响,保证在遍历过程中持有对这些节点的控制权(也就是有位置指针或者能通过
.Next来获得) - 最后就是进行迭代时怎么获得正确的位置,以及最终的结果要返回的是哪个位置。
举个例子,24. 两两交换链表中的节点:
0(虚拟头)-> 1 -> 2 -> 3 -> 4要交换的是12和34
- 交换节点时的第一次操作:
- 0的Next指向2
- 1的Next要改为2的Next
- 2的Next要改为1
- 那么通过上述我们知道,我们至少需要有1前面节点的控制权(因为1和2可以通过
.Next获取),当然实际过程中最好是有两个节点的控制权比较清晰,即0和1的位置 - 当一次操作完成后现在的顺序是
0-> 2-> 1-> 3-> 4,我们要对3、4进行操作,对比一下我们要把在节点0(虚拟头)位置的指针改成1所在位置,在节点1位置的指针改成3所在位置。