本篇题解为此题较简单做法及较少码量,并且码风优良,请放心阅读。
题目简述
给定一个平面内的 \(N\) 个点的坐标,求这 \(N\) 个点中选 \(4\) 个点可构成正方形的方案数。
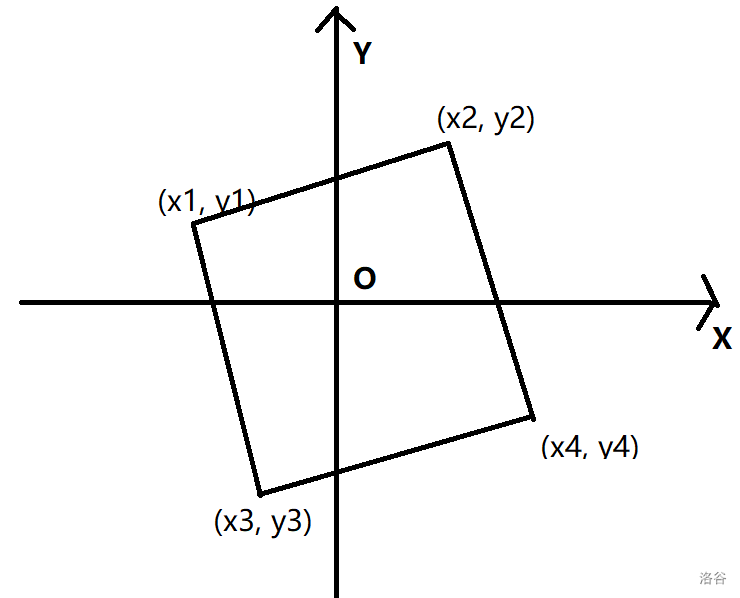
注:构成的正方形的边需平行于 \(x\) 轴或 \(y\) 轴。
例如下图就不符合要求,则不考虑这种情况:
思路
此题基本纯思维题,算法考的不多。
一看数据范围,\(4 \le N \le 2000\)?既然数据范围这么小,那么 \(O(N^2)\) 的时间复杂度是能过的,但如果暴力枚举 \(4\) 个点的话时间复杂度是 \(O(N^4)\),时间复杂度爆炸啊。
所以还是需要一点小优化的,本蒟蒻一开始只想到了枚举 \(3\) 个点,接着判断另一个点是否存在,但这个想法的时间复杂度是 \(O(N^3)\),还是会超时。
那么我们沿袭这个思想就可以想到,直接 \(N^2\) 枚举 \(2\) 的点,接着判断另外两个点是否存在即可,但这枚举的两个点需为两个对角的点,这里我们枚举左上和右下两个点。
接着只需要解决如何判断另外两个点是否存在的问题即可,很容易想到用 map 容器去储存点是否存在的信息。
即可推出判断的语句:\(mp_{x_i,y_i}\) 且 \(mp_{x_j,y_j}\) 且 \(mp_{x_i,y_j}\) 且 \(mp_{x_j,y_i}\) 且 \(x_i<x_j\) 且 \(y_i<y_j\)。
map 容器的初始化直接在输入时初始化即可。
经过以上分析,即可得出代码:
#include<iostream>
#include<map>
using namespace std;
int n, x[2005], y[2005];
long long ans = 0; // 开 long long 好习惯
map<int, map<int, bool> > mp; // 不要写成 >>,中间要有空格
int main() {
cin >> n; // 输入
for(int i = 1; i <= n; i ++) {
cin >> x[i] >> y[i]; // 输入
mp[x[i]][y[i]] = true; // 初始化处理
}
for(int i = 1; i <= n; i ++) {
for(int j = 1; j <= n; j ++) {
if(i == j) continue; // 特判 i = j 的情况
if(mp[x[i]][y[i]] && mp[x[j]][y[j]] && mp[x[i]][y[j]] && mp[x[j]][y[i]] && x[i] < x[j] && y[i] < y[j]) ans ++; // 满足要求 ans++
}
}
cout << ans << endl; // 输出,记得换行
return 0;
}