2020牛客杯NOIP赛前集训提高第一场 T2 牛牛的猜球游戏 题解
目录比赛链接
题目
题目描述
牛牛和牛妹在玩猜球游戏,牛牛首先准备了 \(10\) 个小球,小球的编号从 \(0~9\)。
首先牛牛把这 \(10\) 个球按照从左到右编号为 \(0,1,2,3···9\) 的顺序摆在了桌子上,接下来牛牛把这 \(10\) 个球用 \(10\) 个不透明的杯子倒扣住。
牛牛接下来会按照一定的操作顺序以极快的速度交换这些杯子。
换完以后他问牛妹你看清楚从左到右的杯子中小球的编号了么?
由于牛妹的动态视力不是很好,所以她跑来向你求助。你在调查后发现牛牛置换杯子其实是有一定原则的。
具体来讲,牛牛有一个长度大小为 \(n\) 的操作序列。
操作序列的每一行表示一次操作都有两个非负整数 \(a,b\),表示本次操作将会交换从左往右数第 \(a\) 个杯子和从左往右数第 \(b\) 个杯子(\(a\) 和 \(b\) 均从 \(0\) 开始数)。
请注意是换杯子,而不是直接交换 \(a\) 号球和 \(b\) 号球。
牛牛和牛妹一共玩了 \(m\) 次猜球游戏,在每一轮游戏开始时,他都将杯子中的小球重置到从左往右依次为 \(0,1,2,3···9\) 的状态。
然后在第 \(i\) 轮游戏中牛牛会按照操作序列中的第 \(l_i\) 个操作开始做,一直做到第 \(r_i\) 个操作结束(\(l\) 和 \(r\) 的编号从 \(1\) 开始计算)。
由于你提前搞到了牛牛的操作序列以及每一次游戏的 \(l,r\)。
请你帮助牛妹回答出牛牛每一轮游戏结束时,从左至右的杯子中小球的编号各是多少。
输入格式
首先输入一行两个正整数 \(n,m\),表示操作序列的长度以及进行游戏的次数。
接下来 \(n\) 行每行两个非负整数 \(a,b\),表示交换左数第 \(a\) 个杯子和左数第 \(b\) 个杯子。(\(a,b\) 均从 \(0\) 开始数起)接下来 \(m\) 行每行两个正整数 \(l,r\) 表示该轮游戏中牛牛从第 \(1\) 个操作开始做,一直做到第 \(r\) 个操作结束。(\(l\) 和 \(r\) 的编号从 \(1\) 开始计算)
输出格式
对于每一轮游戏,输出一行 \(10\) 个非负整数,表示从左至右每一个杯子中小球,输出的整数之间用空格隔开,行末不允许有多余空格。
样例
样例1输入
5 3
0 1
1 2
2 3
0 1
9 0
1 5
5 5
3 5
样例1输出
9 1 3 0 4 5 6 7 8 2
9 1 2 3 4 5 6 7 8 0
9 0 3 2 4 5 6 7 8 1
数据范围
对于 \(30\%\) 的测试数据,保证 \(1≤n,m≤500\)
对于 \(60\%\) 的测试数据,保证 \(1≤n,m≤4\times10^4\)
对于 \(60\%\) 以外另 \(10\%\) 的测试数据,保证 \(a,b\in\{0,1,2\}\)
对于 \(100\%\) 的测试数据,保证 \(1≤n,m≤10^5,0≤a,b≤9,1≤l≤r≤n\)
分析
我们从数据范围入手进行分析:\(n\) 和 \(m\) 的最大值是 \(10^5\),也就是说用 \(n\times\sqrt n\) 的笨办法稍微卡卡常数就能过,而我们又发现这道题总共也就是 \(10\) 个球在换来换去,交换的方法也就是那 \(n\) 种,所以我们理所当然的想到了分块暴力。旁边有巨佬说莫队也可以,奈何我太菜了写不来
思路
所谓分块,就是将本来 \(10^5\) 次的交换操作拆分成一个一个\(_{(?)}\)的区间并提前预处理好,这样当我们重复进行多次计算时遇到这些区间就可以直接读取结果跳过。如下图:

这样的操作乍看来对程序的提升不大,但当要求的操作次数(如题目中的 \(m\))很大而且操作总数(如题目中的 \(n\))很大时,分块思想对程序的提升相当明显。
那么我们运用这样的思路来分析这道题:
我们在读入每步操作之后,对总共 \(n\) 步操作进行预处理,将其拆分成 \(\sqrt n\) 个 \(\sqrt n\) 步操作组成的区间。
这样的话,我们在进行从 \(l\) 到 \(r\) 的操作的时候,只需要从 \(l\) 处理到下一个区间开始的地方,套用区间预处理的结果一直到 \(r\) 前最后一个区间,再按照普通的方法处理剩下的操作就行了。可以参照下图理解:
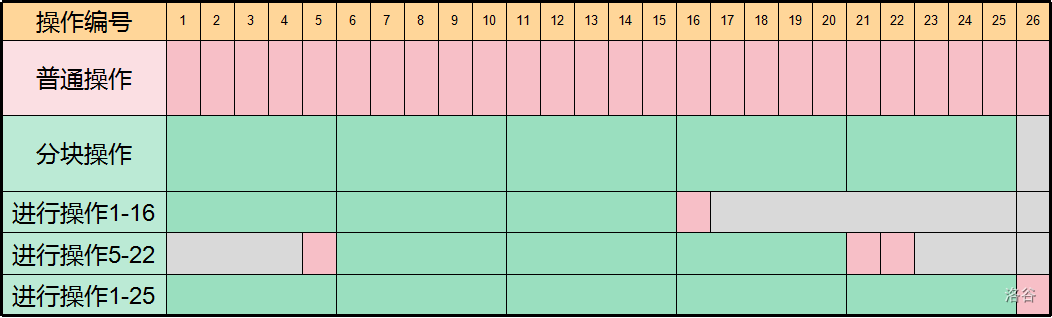
接下来,我们还需要解决如何存储每块的结果。我们定义一个长度为 \(10\) 的数组 \(A[i]\) 分别存储原来在第 \(i\) 个位置的杯子在进行完区间内的操作后的位置。如下图:
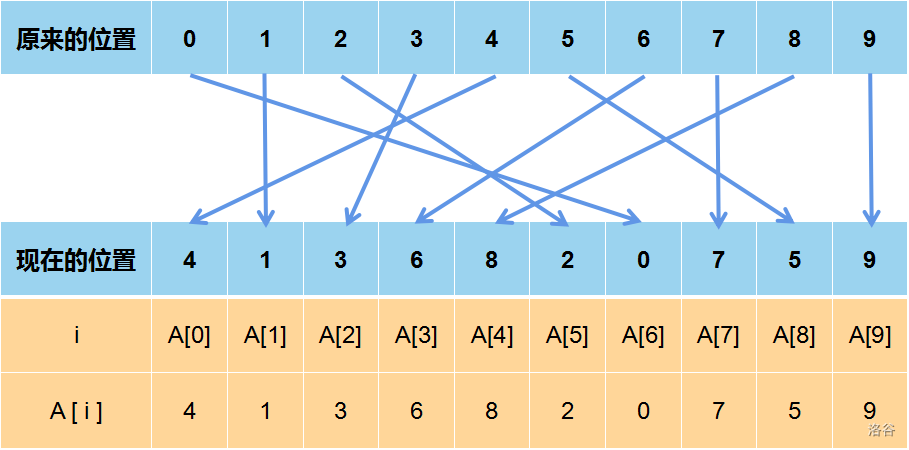
优化 卡常
对于题目中的 \(10^5\),最多只会被分成316个区间,每个区间316个数,对于最差情况处理 \(l\) 到第一个区间左端及最后一个区间右端到 \(r\) 的距离为 \(2\times315=630\) ,最大时间复杂度 \(10^5\times(630+316)\approx10^7\) ,我们稍微卡一下常数勉强能过。至于卡常的方法呢……
| 优化项目(单项) | 优化后时间(同数据五次平均值) |
|---|---|
| 无优化 | 3.4294 s |
scanf → getchar |
3.1618 s |
printf → putchar |
1.1348 s |
int → register int |
3.3127 s |
void → inline void |
3.3228 s |
O2 |
2.7832 s |
| 综合优化 | 0.3742 s |
好啦!现在我们就能愉快的过啦!
代码
为了增强代码的可读性,删除了 register 等优化并手打了一些空格。
#include<cstdio>
#include<math.h>
using namespace std;
int movemem[400][10];//存储分的块
int N, M, sqrtN, L, R;
int getnum()//快读
{
int x = 0, f = 1;
char c = getchar();
while( c<'0' || c>'9' )
{
if( c=='-' )
f=-1;
c = getchar();
}
while( c >= '0' && c <= '9' )
{
x = ( x<<1 ) + ( x<<3 ) + ( c^48 );
c = getchar();
}
return x*f;
}
void Copy( int a[] , int b[] )//复制数组
{
for( int i = 0 ; i <= 9 ; i ++ )
a[i] = b[i];
return;
}
void Swap( int &a , int &b )//交换两个数
{
int temp = a;
a = b;
b = temp;
return;
}
struct Oper//每步操作的左右杯子位置(你也可以用两个数组或者其他啥东东存)
{
int l, r;
}oper[100005];
int main()
{
N = getnum();
M = getnum();
sqrtN = sqrt( N );//N开方作为分块大小及个数
for( int i = 1 ; i <= N ; i++ )//读入每步操作的左右位置
{
oper[i].l=getnum();
oper[i].r=getnum();
}
for( int i = 1 ; i <= (N/sqrtN) ; i++ )//预处理,进行分块
{
int n[10] = {0,1,2,3,4,5,6,7,8,9};//就是上面讲的A[i]
for( int j = 1 ; ((j<=sqrtN) && (sqrtN*(i-1)+j<=N)) ; j++ )
{// 最后一个分块不能超过N的范围 ↑
Swap( n[oper[sqrtN*(i-1)+j].l] , n[oper[sqrtN*(i-1)+j].r] ); //预处理
}
Copy( movemem[i] , n );//存储每一块的最终结果
}
for( int i=1 ; i<=M ; i++ )//进行每一轮游戏
{
L = getnum() , R = getnum();//读入每轮游戏的操作开头和结尾
int n[10] = {0,1,2,3,4,5,6,7,8,9} , ans[10];//ans[]用于过程中临时存储
for( int j = L ; j <= R; j++ )
{
if( ((j-1)%sqrtN==0) && (j+sqrtN<=R) )
{//若遇到一个块的开头且这个块的结尾在这轮游戏的操作结尾之前就直接调用分块答案
for( int k=0 ; k<=9 ; k++)
{
ans[k] = n[ movemem[ j/sqrtN+1 ][ k ] ];//调用分块答案
}
j += sqrtN-1;
Copy( n , ans );//将答案合并
}
else//如果没遇到哪个块的开头
{
Swap( n[oper[j].l] , n[oper[j].r] );//进行暴力模拟
}
}
for( int j = 0 ; j <= 9 ; j++ )
{
putchar( n[j]+'0' ),putchar( ' ' );//putchar快速输出
}
putchar( '\n' );
}
return 0;
}
最后……
写的这么好的题解不给个赞吗 (〃'▽'〃)
其他的思路:
标签:10,游戏,牛牛,题解,7605T2,区间,操作,杯子 From: https://www.cnblogs.com/if-OF/p/nowcoder-7605-T2.html