这个人赛时只过了这题,但是同学 @sinsop90 赛时只没过这题,怎么会是呢?
考虑到 \(s,t\) 之间路径必须经过关键点,假设这个关键点为 \(k\),那么路径形式一定是 \(s\to k\to t\)(废话)。
画一下图发现这条路径的长度等于 \(s\to t\) 的简单路径长度加上 \(k\) 挂到 \(s\to t\) 简单路径这条链上所经过的路径长度的 \(2\) 倍。
即:
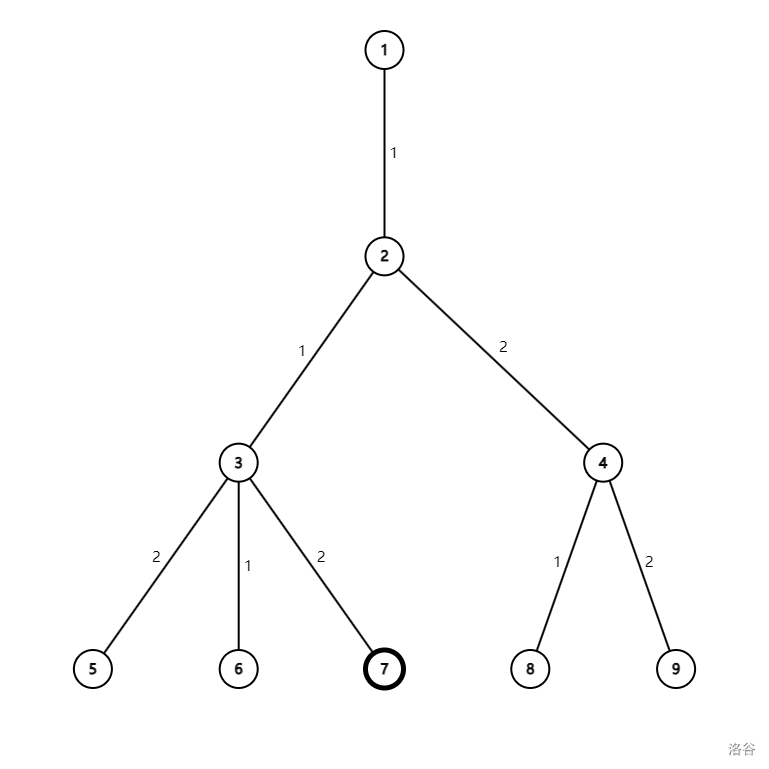
考虑 \(1\to 7\to 9\) 这条路径,其长度相当于 \(1\to 2\to 4\to 9\) 简单路径长度加上 \(7\to 3\to 2\) 这条路径长度的 \(2\) 倍。
设 \(S\) 为关键点的集合,\(d(k,s\to t)\) 表示 \(k\) 挂到 \(s\to t\) 路径的长度。
对于一个询问 \((s,t)\),\(s\to t\) 路径长度时容易求的,我们只需要计算 \(\min\limits_{k\in S}d(k,s\to t)\) 即可。
考虑到 \(k\) 挂到 \(s\to t\) 路径上的那个点是唯一且在路径 \(s\to t\) 上的(上图中 \(k=7,s=1,t=9\),\(7\) 挂到 \(1\to 9\) 的点是 \(2\)),可以预处理出对于每个点 \(u\),离它最近的关键点的距离 \(f_u\),那么 \(\min\limits_{k\in S}d(k,s\to t)=\min\limits_{u\in \{s\to t\}}f_u\),\(\{s\to t\}\) 表示 \(s\to t\) 简单路径上的点构成的集合(包括 \(s,t\))。
这个 \(f_u\) 显然可以通过树形 dp 求出,问题转换为求 \(s\to t\) 路径上的点的 \(f\) 值的最小值,树剖解决即可。因为我用的是线段树,复杂度 \(O(n\log^2 n)\),其实可以 st 表做到 \(O(n\log n)\)。
赛时代码,写得有点丑陋。
标签:路径,limits,min,Hard,rStage5,挂到,NAPC,长度,关键点 From: https://www.cnblogs.com/Ender32k/p/17569338.html