振幅法测向即为对天线接收到的信号幅度信息进行分析处理,以获得信号角度信息的方法,主要分为波束搜索法(最大振幅法)和全向振幅单脉冲测向法。
**
- 1
- 2
1.波束搜索法
** 波束搜索法的原理图如1所示。接收天线从以v的速度在一定搜索角度内顺时针旋转,当天线接收到的信号幅度高于检测门限时,记下此时旋转角度theta1;继续旋转,当天线接收到的信号幅度低于检测门限时,记下此时的旋转角度为theta2。因为当接收天线和辐射源角度重合越多,接收到的信号幅度越大,故令1/2(theta1+theta2)为测向角。不难看出,虽然利用该法测向操作简单,但是不易选择门限值,这也导致测向误差可能会很大。

2.全向振幅单脉冲测向法
测向系统框图如图2所示,测向天线以圆阵的形式均匀分布在360度的范围内,再根据天线输出的信号幅度信息求得信号方位角。

2.1 相邻比幅法
以相邻比幅法为例进行测向。如图3所示为相邻比幅法的天线方向图,假设接收信号的均匀圆阵由N个天线组成,则相邻天线的夹角theta_s=360/pi;且假设圆阵中的天线方向图满足对称性,即F(theta) = F(-theta)。fai为欲测向方位角(注:图3摘自学位论文《无人机目标无源定位方法研究》)
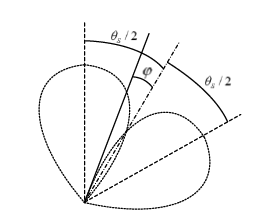
通常令F(theta)=exp(-k*theta^2),即高斯函数,其中,半功率波束宽度的定义为F(theta_r/2)=1/squrt(2);带进去可得
F(theta) = exp(-1.3835(theta/theta_r)^2)。
因此,可以求得两个天线各自的输出信号s1和s2。其中s1=lg[K1*F(theta_s/2-fai)*A];s2=lg[K2*F(theta_s/2+fai)*A](A为方向矢量,K为各通道幅度响应)。
令s1-s2可得,s1-s2=lg[K1*F(theta_s/2-fai)/(K2*F(theta_s/2+fai))];
再令R=10(s1-s2).(通常都写为10lg,此处可不用这么写)
再令K1=K2,且将F带入R中,可得 fai=theta_r^2*R/(12*theta_s), 具体推导如图所示
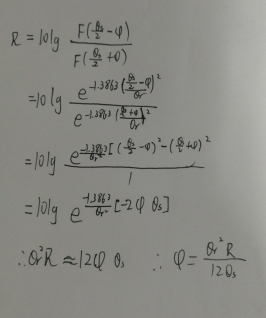
2.2 全向比幅法
F(theta)=exp(-k*theta^2),求其傅里叶级数展开式。(注:由于其为偶函数,故bn=0,只求an即可),得到公式如图所示。

又因为要根据所有方向天线接收到的信号进行分析处理,故对每个方向输出加权之后再求和,权值为cos(theta_s*i)及·sin(theta_s*i),得到的公式如图所示。
`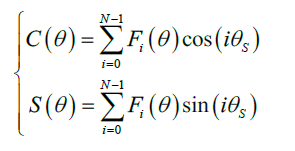
将F带入,并通过和差化积可得:
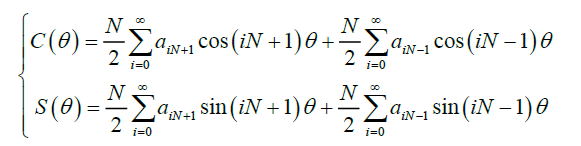
近似取得
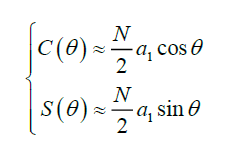
故可求得方位角为
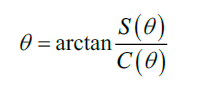
2.3 相邻比幅法的MATLAB实现
MATLAB代码如下:
% 参数设置 % 天线阵列为2,信号的角度为30,信噪比为10,信号长度为n=500。 theta=30; % 信号来波角度 j = sqrt(-1); % 产生虚数符号 M = 2; % 阵元数/天线数 dd = 0.5; d = 0:dd:(M-1)*dd; iwave = 1; % 几个来波 snr = -20; n = 500; A = exp(-j*2*pi*d.'*sin(theta* pi / 180)); % 方向矢量 S = randn(iwave,n); x = A*S; X = awgn(x,snr,'measured'); % X 为产生的信号%------------------------------------------%
% 假设天线的波束宽度为45,则半波束宽度为22.5,
H_theta = 22.5;
A_theta = 45;
F_theta = 22.5;
S_theta = 67.5;
k = -1.3863;
M_theta = (F_theta+S_theta)/2;
R_theta = theta - M_theta;
F1 = exp(k(R_theta+M_theta)2/(H_theta2)); % 天线方向图
F2 = exp(k(R_theta-M_theta)2/(H_theta2));
S1 = F1.X(1,:);
S2 = F2.X(1,:);
%-----------------------------------------%
%A = F1/F2;
A = abs(S1/S2);
R = 10log10(A);
R_angle = H_theta^2/(24A_theta)*R;
angle = M_theta-R_angle;
es = theta - angle;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
