7.17后记

P6090 题解

传送门

神仙题

先考虑 \(O(|\Sigma| ^8)\) 做法：

\(\Sigma\)：字符总数，本题为 大写字母 \(26\) 个+小写字母 \(26\) 个+数字 \(10\) 个。

预处理两个字母一首一尾可以组成多少种长度相同的字符串，枚举正方体 \(8\) 个顶点，计算每两个点之间贡献的积。

for (int a1 = 1; a1 <= 62; a1++)
    for (int a2 = 1; a2 <= 62; a2++) 
        ...
            for (int a8 = 1; a8 <= 62; a8++) 
                ans += v[a1][a2] * v[a1][a3] * ... * v[a7][a8];

再考虑 \(O(|\Sigma| ^7)\) 做法：

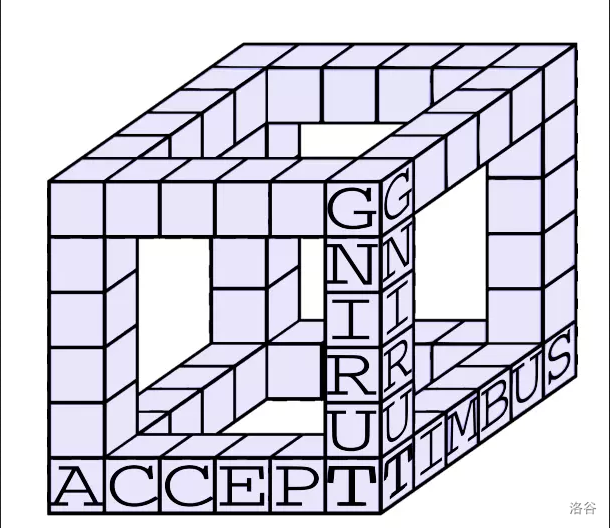
图中点 \(G\)，\(A\)，\(T\)，\(S\) 之间三条边的贡献可以提前用 \(O(\sum ^4)\) 的复杂度预处理出来，

for (int l = 1; l <= 62; l++) 
	for (int i = 1; i <= 62; i++) 
		for (int j = 1; j <= 62; j++) 
			for (int k = 1; k <= 62; k++) 
				f[i][j][k] += v[l][i] * v[l][j] * v[l][k];

就只用枚举 \(7\) 个点了。

再推广一下，

我们可以把正方体分成 \(4\) 部分，每一部分都能用上面的预处理直接得出答案，就只用枚举体对角线的 \(4\) 个点了，复杂度 \(O(|\Sigma| ^4)\)。

注意：不同长度要分开处理

卡常优化小技巧

不影响答案时，多层循环时最后一层循环最好和循环内多维数组的最后一个下标对应，如图：

这样读取数组时是从 CPU 缓存直接读取的，速度更快。

经过折磨的测试，不这么写会喜提 TLE。

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 5, mod = 998244353;

int n, ans;
int cnt[11];
int v[11][63][63];
int f[11][63][63][63];

int tran(char c) {
	if (c >= 'a' && c <= 'z') return c - 96;
	else if (c >= 'A' && c <= 'Z') return c - 38;
	else if (c >= '0' && c <= '9') return c + 5;
	else return 0;
}

string s[maxn];

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> s[i];
		s[i + n] = s[i];
		reverse(s[i + n].begin(), s[i + n].end());
	}
	n *= 2;
	sort(s + 1, s + 1 + n);
	n = unique(s + 1, s + n + 1) - s - 1;//去重
	for (int i = 1; i <= n; i++) {
		cnt[s[i].size()]++;
		v[s[i].size()][tran(s[i][0])][tran(s[i][s[i].size() - 1])]++;
	}
	for (int len = 3; len <= 10; len++) {
		if (!cnt[len]) continue;
		for (int l = 1; l <= 62; l++) {
			for (int i = 1; i <= 62; i++) {
				if (!v[len][l][i]) continue;
				for (int j = 1; j <= 62; j++) {
					if (!v[len][l][j]) continue;
					for (int k = 1; k <= 62; k++) {
						if (!v[len][l][k]) continue;
						(f[len][i][j][k] += 1ll * v[len][l][i] * v[len][l][j] % mod * v[len][l][k] % mod) %= mod;
					}
				}
			}
		}
		for (int l = 1; l <= 62; l++) {
			for (int i = 1; i <= 62; i++) {
				for (int j = 1; j <= 62; j++) {
					if (!f[l][i][j]) continue;
					for (int k = 1; k <= 62; k++) {
						(ans += 1ll * f[len][i][j][k] * f[len][i][j][l] % mod * f[len][i][k][l] % mod * f[len][j][k][l] % mod) %= mod;
					}
				}
			}
		}
	}
	cout << ans;
	return 0;
}

Tenzing and Triangle

线段树优化 \(dp\)（大雾）

Wonderful Jump

文文的摄影布置

区间中寻找三元组（i,j,k），使得 \(A_i-B_j+A_k\) 最大

算术天才⑨与等差数列

等差数列（公差为 \(k\) ）\(\rightarrow\) %\(k\) 相同

判重：维护 \(\text{pre[i]}\) 记录 \(i\) 点前第一个与 \(i\) 相等的位置

每个值开 \(set\) ，记录值在序列上位置，方便修改 \(pre\)

区间gcd

1. 信息 + 信息
2. 标记 + 标记
3. 信息 + 标记

方差

维护区间平方和

P不知道多少

二维数点