云斗杯 T2 题解
赛时脑抽了只打了 60pts 暴力 xwx。
题目描述
给定两个长度为 \(n\) 的 \(01\) 序列 \({a_n}\) 和 \({b_n}\),与另一个矩阵 \({c_{n,n}}\)。矩阵 \({c_{n, n}}\) 的生成规则如下:
\[c_{i, j} = a_i \times b_j \]现给定一个数 \(k\),求在矩阵 \(c_{n, n}\) 内,有多少个连续子矩阵满足其中有 \(k\) 个 \(1\)?
样例 #1
样例输入 #1
4 4
0 1 1 1
1 0 1 0
样例输出 #1
6
样例解释
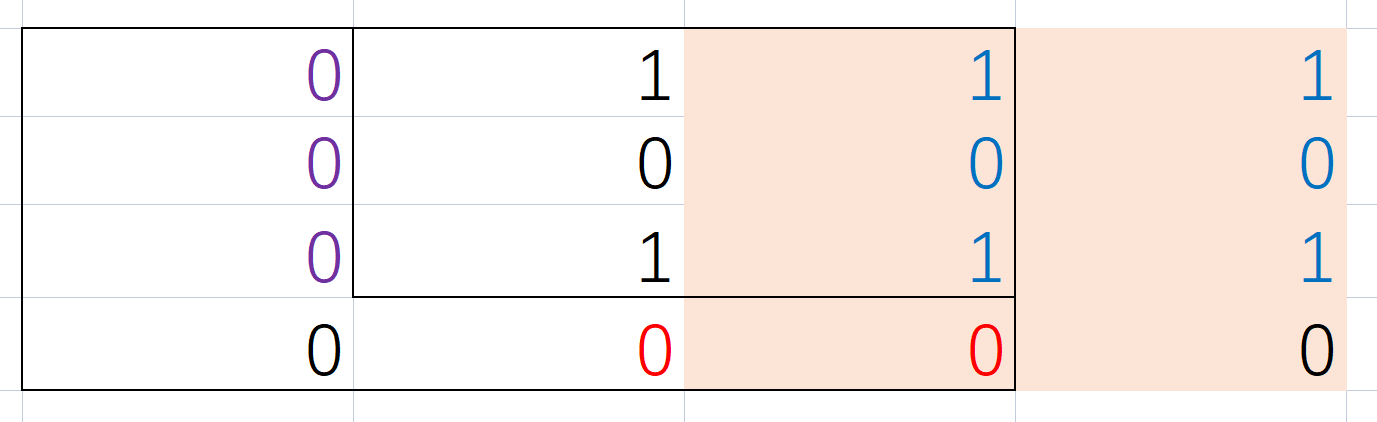
如图,取蓝色字部分、米色背景部分、两个粗线框内部,以及小粗线框加上紫色或绿色的 \(0\) 构成的矩阵均符合题意。
数据范围
$1 \leq n \leq 3 \times 10^5, 1 \leq k \leq 10^{12} $
思路
首先看到 \(n\) 的范围意识到这个矩阵没法直接求出来,只能转化题意。
然后我们来考虑一个包含 \(k\) 个 \(1\) 的矩阵应该怎样生成,发现,一个子矩阵包含 \(k\) 个 \(1\),当且仅当这个子矩阵对应的两个序列中的区间和乘积为 \(k\)。这个结论很好证明,因为每一个 \(a\) 中的 \(1\) 都可以与 \(b\) 中对应列上的 \(1\) 生成一个 \(1\)。
那么,现在问题就转化为了求两个序列中,区间和为 \(k\) 的某个因数的区间的个数。如果暴力去 \(dp\),会发现要 \(n^2\) 枚举。但是,这样做会枚举到很多没用的数,且会浪费很多信息。我们又知道,\(10^{12}\) 以内的数最多有 \(6720\) 个不同的因数;而且,\(n\) 只有 \(3 \times 10^5\),这也就意味着,有很多 \(k\) 的因数是超出 \(n\) 的范围的。所以,我们直接枚举 \(k\) 的所有因数,然后用前缀和+双指针直接处理即可。
代码:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 3e5+100;
const int mod = 998244353;
inline ll read(){
ll x = 0; char ch = getchar();
while(ch<'0' || ch>'9') ch = getchar();
while(ch>='0'&&ch<='9') x = x*10+ch-48, ch = getchar();
return x;
}
int a[N], b[N];
ll sa[N], sb[N];
int n; ll K;
ll fa[N], fb[N];
ll yin[10000], toty;
int main(){
n = read(), K = read();
for(ll i = 1; i*i<=K; ++i){
if(K%i) continue;
yin[++toty] = i;
if(K/i!=i) yin[++toty] = K/i;
}
for(int i = 1; i<=n; ++i){
a[i] = read();
sa[i] = sa[i-1]+a[i];
}
for(int i = 1; i<=n; ++i){
b[i] = read();
sb[i] = sb[i-1]+b[i];
}
// for(int i = 1; i<=n; ++i){
// for(int j = 1; j<=i; ++j){
// ++fa[sa[i]-sa[j-1]];
// }
// }
// for(int i = 1; i<=n; ++i){
// for(int j = 1; j<=i; ++j){
// ++fb[sb[i]-sb[j-1]];
// }
// }//暴力部分 xwx
int ans = 0;
for(ll i = 1; i<=toty; ++i){
ll yina = yin[i], yinb = K/yin[i];
if(yina > sa[n] || yinb > sb[n]) continue;
ll tmpa = 0, tmpb = 0;
for(int l = 1, r = 1, ta = 0, tb = 0; r<=n; ++r){
if(sa[r] < yina) continue;
while(sa[r]-sa[l-1] > yina) ++l, ++ta;
if(sa[r]!=sa[r-1]){
tmpa = (tmpa+1ll*ta*tb%mod)%mod;
ta = 0, tb = 0;
}
++tb;
if(r == n){
while(sa[r]-sa[l-1] == yina) ++l, ++ta;
tmpa = (tmpa+ta*tb%mod)%mod;
}
}
for(int l = 1, r = 1, ta = 0, tb = 0; r<=n; ++r){
if(sb[r] < yinb) continue;
while(sb[r]-sb[l-1] > yinb) ++l, ++ta;
if(sb[r]!=sb[r-1]){
tmpb = (tmpb+ta*tb%mod)%mod;
ta = 0, tb = 0;
}
++tb;
if(r == n){
while(sb[r]-sb[l-1] == yinb) ++l, ++ta;
tmpb = (tmpb+1ll*ta*tb%mod)%mod;
}
}
ans = (ans+1ll*tmpa*tmpb)%mod;
}
// for(int i = 1; i<=n; ++i){
// if(K%i) continue;
// if(i>sa[n]) continue;
// ll tmp = K/i;
// if(tmp>sb[n]) continue;
// ans = (1ll*ans+1ll*fa[i]*fb[tmp]%mod)%mod;
// }
printf("%d\n", ans);
return 0;
}