插头 DP,是一类解决网格图上连通性问题的状压 DP。
相关概念
轮廓线:已经决策的方格和未决策方格之间的分界线。
插头:用来描述连通性,一个方格与其某一方向的相邻方格连通,则称这个方格有某个方向的插头。容易发现在轮廓线上,每个时刻都是有 \(n\) 个上插头与 \(1\) 个左插头。
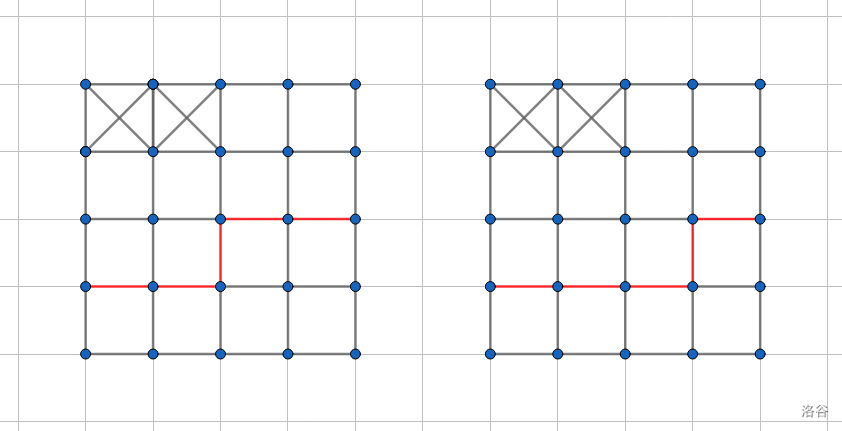
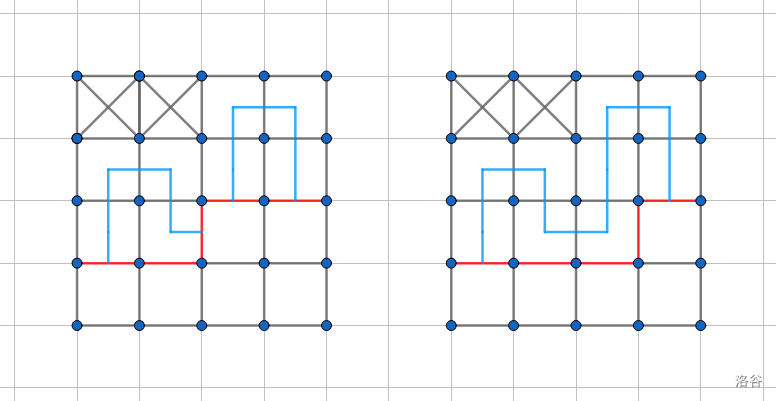
如图,红线部分为 \((3,3)\) 决策前后的轮廓线。
括号表示法
对于连通性问题,需要将当前的插头的状态进行压缩用于转移。
在哈密顿回路问题中,插头一定两两配对,且不存在相交关系,因此可以用括号表示法,将当前路径的左端插头设为 ( 并用 \(1\) 表示,右端插头设为 ) 并用 \(2\) 表示,不含插头的位置则用 0 表示。
在哈密顿路径问题中,插头可能独立存在,将这样路径设为 () 并用 \(3\) 表示。
由于合法的括号序列个数小于 \(4^{m+1}\),因此可以使用手写哈希表来减少空间,转移之和上一个方格相关,因此类似滚动数组的开两个哈希表即可。
状态转移
以 模板题 为例。
注意到左插头和上插头(如果存在)转移后分别变成了上插头和左插头(如果存在),且在括号序列的位置不变,转移时只需要考虑当前的两个插头即可。
设当前决策方格的左插头为 \(p_1\),上插头为 \(p_2\)。
特判当前方格存在障碍的情况,此时 \(p_1,p_2\) 必须均为 \(0\),转移后同样均为 \(0\)。
以下转移均以当前方格以及与当前方格存在插头的方格均不存在障碍为前提。
- 若 \(p_1,p_2\) 均为 \(0\),转移相当于新建一个连通块,当前方格需要向下向右都连通,转移后 \(p_1=1,p_2=2\)。
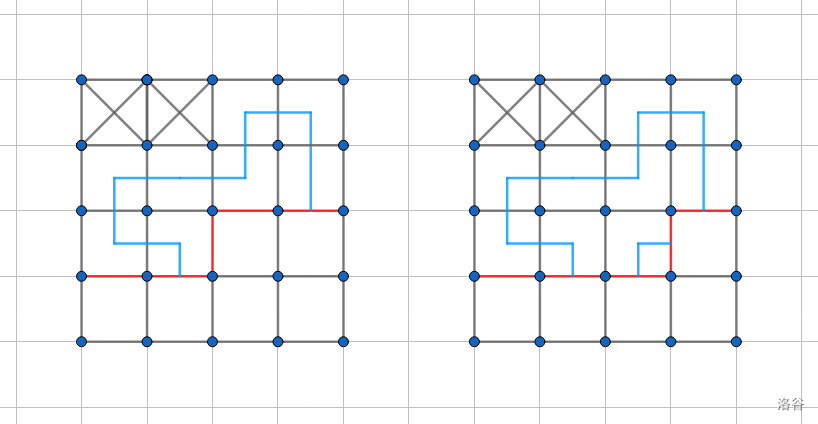
- 若 \(p_1\) 不为 \(0\),\(p_2\) 为 \(0\),转移相当于拓展一个连通块,向下或向右有两种情况。
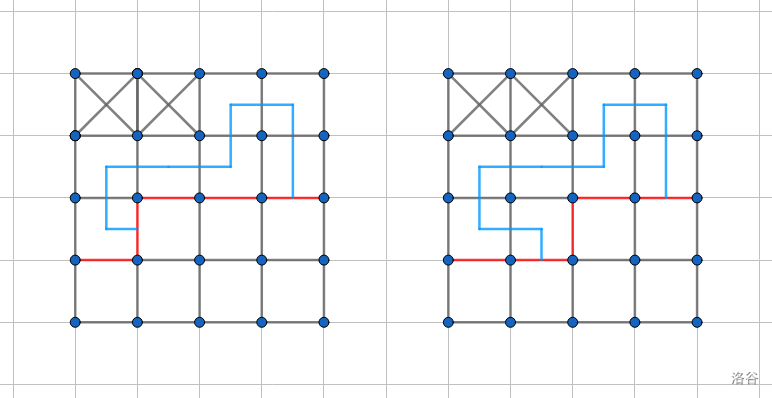
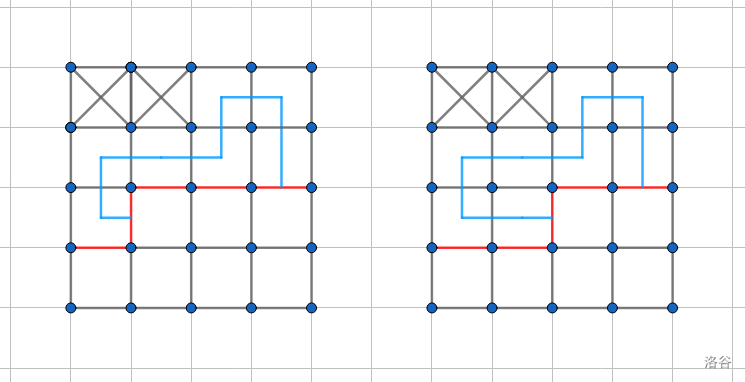
- 若 \(p_1\) 为 \(0\),\(p_2\) 不为 \(0\),同理也有两种情况。
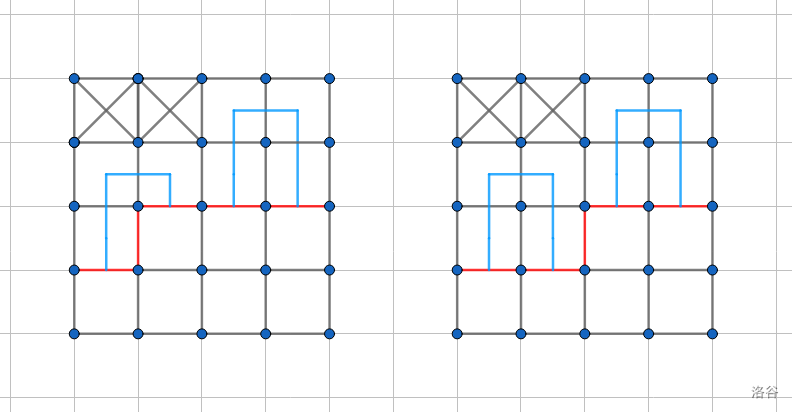
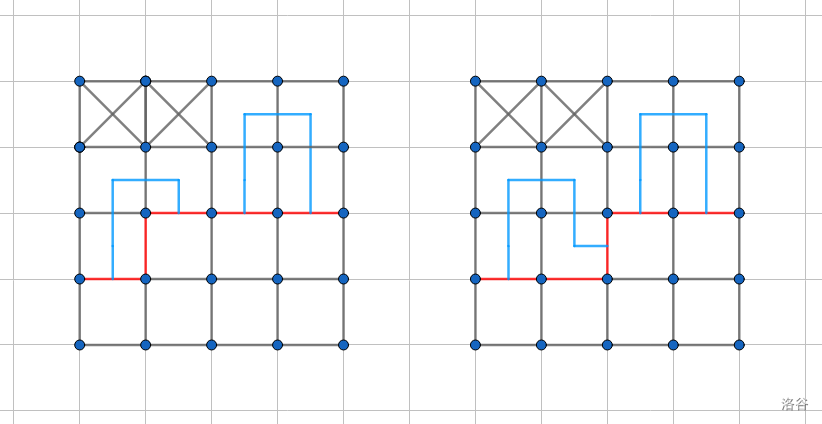
- 若 \(p_1=1,p_2=1\),转移相当于合并两个连通块,此时 \(p_2\) 对应的右括号变成左括号。
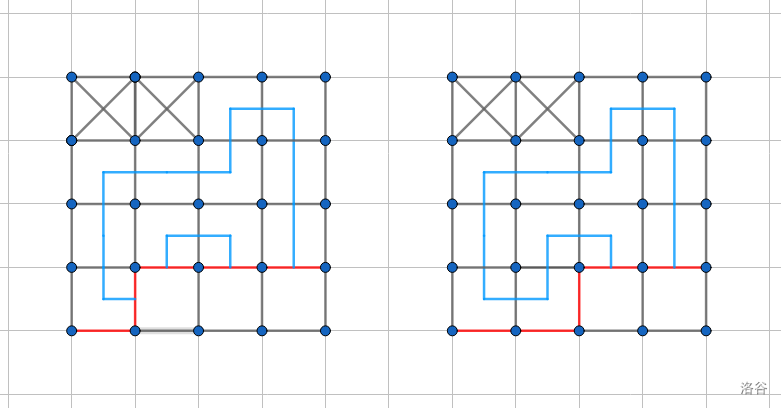
- 若 \(p_1=2,p_2=2\),同理,此时 \(p_1\) 对应的左括号变成右括号。
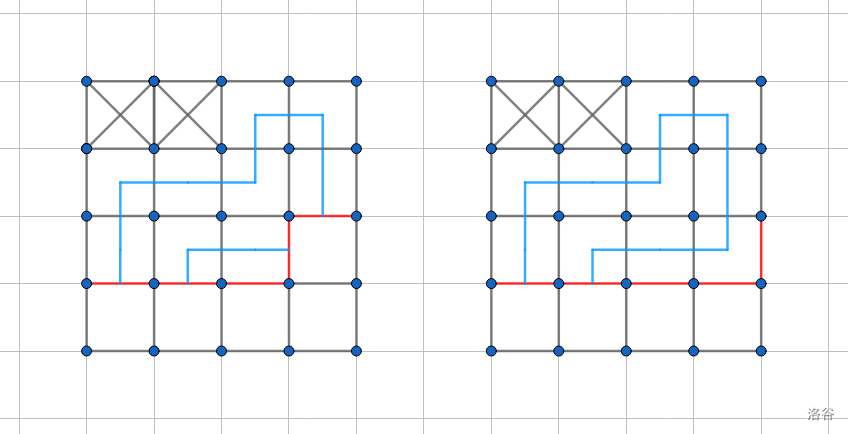
- 若 \(p_1=2,p_2=1\),二者直接合并。
- 若 \(p_1=1,p_2=2\),回路闭合。

当切换一行时,注意到左插头从最后一位移至第一位,需要改变状态。
点击查看代码
int n,m;
char mp[15][15];
int ex,ey;
int head[mod+10],nxt[maxn];
int st[2][maxn],cnt[2];
ll dp[2][maxn],ans;
inline void update(int now,int s,ll val){
int p=s%mod+1;
for(int i=head[p];i;i=nxt[i]){
if(st[now][i]==s) return dp[now][i]+=val,void();
}
st[now][++cnt[now]]=s,dp[now][cnt[now]]=val;
nxt[cnt[now]]=head[p],head[p]=cnt[now];
}
int main(){
n=read(),m=read();
for(int i=1;i<=n;++i){
scanf("%s",mp[i]+1);
for(int j=1;j<=m;++j){
if(mp[i][j]=='.') ex=i,ey=j;
}
}
int now=0;
update(now,0,1);
for(int i=1;i<=n;++i){
for(int k=1;k<=cnt[now];++k) st[now][k]<<=2;
for(int j=1;j<=m;++j){
memset(head,0,sizeof(head));
now^=1;
cnt[now]=0;
for(int k=1;k<=cnt[now^1];++k){
int s=st[now^1][k];
ll val=dp[now^1][k];
int p1=(s>>2*(j-1))&3,p2=(s>>2*j)&3;
int t=s-(p1<<2*(j-1))-(p2<<2*j);
if(mp[i][j]=='*'){
if(!p1&&!p2) update(now,s,val);
}
else{
if(!p1&&!p2){
if(mp[i+1][j]=='.'&&mp[i][j+1]=='.') update(now,t+(1<<2*(j-1))+(2<<2*j),val);
}
else if(p1&&!p2){
if(mp[i+1][j]=='.') update(now,s,val);
if(mp[i][j+1]=='.') update(now,t+(p1<<2*j),val);
}
else if(!p1&&p2){
if(mp[i+1][j]=='.') update(now,t+(p2<<2*(j-1)),val);
if(mp[i][j+1]=='.') update(now,s,val);
}
else{
if(p1==1&&p2==1){
int tmp=1;
for(int l=j+1;l<=m;++l){
if((s>>(2*l)&3)==1) ++tmp;
if((s>>(2*l)&3)==2) --tmp;
if(!tmp){
update(now,t-(1<<2*l),val);
break;
}
}
}
else if(p1==2&&p2==2){
int tmp=1;
for(int l=j-2;l>=0;--l){
if((s>>(2*l)&3)==2) ++tmp;
if((s>>(2*l)&3)==1) --tmp;
if(!tmp){
update(now,t+(1<<2*l),val);
break;
}
}
}
else if(p1==2&&p2==1){
update(now,t,val);
}
else{
if(i==ex&&j==ey) ans+=val;
}
}
}
}
}
}
printf("%lld\n",ans);
return 0;
}
参考资料
-
《基于连通性状态压缩的动态规划问题》 - 陈丹琦