一些杂题,主要是贪心(模拟费用流)。
Bohater
有 \(n\) 只怪物,为了打败第 \(i\) 只怪物,你会下降 \(d_i\) 的血量。击败怪物后,会掉落回复 \(a_i\) 生命值的血药。任何时刻血量都不能小于等于 \(0\)。问是否存在一种打怪顺序使得自身不死掉。
数据范围:\(n \le 10^5\)。
简单贪心,我们把怪物分为两种类型:击败后加血和击败后扣血。对于第一种怪物,我们可以采取先打 \(d_i\) 小的,因为我们需要攒血量去打 \(d_i\) 大的怪物。对于第二种怪物,我们倒着考虑。我们这样就可以发现,倒着看时,\(d_i\) 为血药,\(a_i\) 为减小的血量,为了使得血量不小于 \(0\),我们需要把减少的血量小的放前面,在原顺序中也就是把 \(a_i\) 小的放后面。
不离
有 \(2\) 个属性 \(x\) 和 \(y\) 以及 \(n\) 件装备,第 \(i\) 件装备需要在 \(x \ge a_i, y \ge b_i\) 时才能穿上,穿上后会使 \(x\) 加上 \(c_i\),使 \(y\) 加上 \(d_i\)。如果想让所有装备都穿上,最初的 \(x\) 最小应该是多少。在 \(x\) 最小的前提下,\(y\) 最小是多少。
数据范围:\(n\le 10^5\)。
我们先考虑 \(x\)。我们可以先把装备按 \(a_i\) 排序,一件一件穿。当 \(x\) 无法达到 \(a_i\) 时,我们就提升初始的 \(x\),把这段差值补上。这样就求出了最小的初始 \(x\)。
我们再考虑 \(y\)。既然有了初始的最小 \(x\),我们就可以模拟穿装备的过程。一件一件穿,当力量值大于 \(a_i\) 时,我们把这件装备扔到按 \(b_i\) 排序的堆里。当力量值小于 \(a_i\) 时,我们再从堆里一件一件拿装备穿,过程和求 \(x\) 的过程一样。由于 \(x\) 是我们求出的最小解,因此一定有解。
专业网络
有 \(n\) 个人,可以花费 \(b_i\) 元和这个人成为朋友,也可以在朋友数超过 \(a_i\) 时和它成为朋友。询问和这些人成为朋友的最小花费。
数据范围:\(n\le 2\times 10^5\)。
你谷评分逆天,2400评绿
我们考虑能够最多节约多少钱。我们先把所有人按照 \(a_i\) 排序,这时我们发现正着考虑不太好,因为我们花钱一定是买 \(a_i\) 更大的,因此我们从后往前考虑。我们先认为所有人都是花钱买的,我们遇到一个人先把它扔到堆里,同时把他的钱节约下来,让他成为不通过花钱交上朋友的人。如果我们发现当前 \(a_i\) 要大于现在买的人数,那我们就取出堆顶,把他买下来。这样就完成了。
说着简单想起来是真难
排列鞋子
有 \(n\) 双鞋子,分左右鞋,放在编号为 \(0\sim 2n-1\) 的位置上。我们要求最终的序列为:编号 \(2i\) 位置上的鞋子是左鞋,编号为 \(2i+1\) 的位置上的鞋子是右鞋,并且编号 \(2i\) 和 \(2i+1\) 的位置上的鞋子的大小相等。每次可以交换相邻的两只鞋子,问最少交换多少次可以满足上面的条件。
数据范围:\(n\le 10^5\)。
我们可以从右往左扫这个序列,遇到没有用过的鞋子就在它左边找到和它配对的,把那只鞋子移过来即可。我们来证明一下这个算法的正确性。
首先,如果我们要把这两只鞋子移动到一起,如果最终移动到的位置在这两个鞋子之间,那么操作次数不变。我们考虑对其他鞋子的影响。首先对左半部分的鞋子不会有影响,它们的位置不变。而对于在这两个鞋子之间的鞋子 \(x\),如果与它配对的鞋子在最终移动到的位置的右边,则操作数不变,如果在最终移动到的位置的左边,则操作数会增加。则我们需要尽可能减少这样的情况出现。而移动到最右端时这样的情况就会变为 \(0\)。因此这样是最优的。
这样就可做了。用一个树状数组统计答案即可。
Buy Low Sell High
已知接下来 \(n\) 天的股票价格,每天你可以买进一股股票,卖出一股股票,或者什么也不做。最终最多能赚多少钱。
数据范围:\(n\le 3\times 10^5\)。
模拟费用流开始
本题很容易建出费用流模型。见下图。
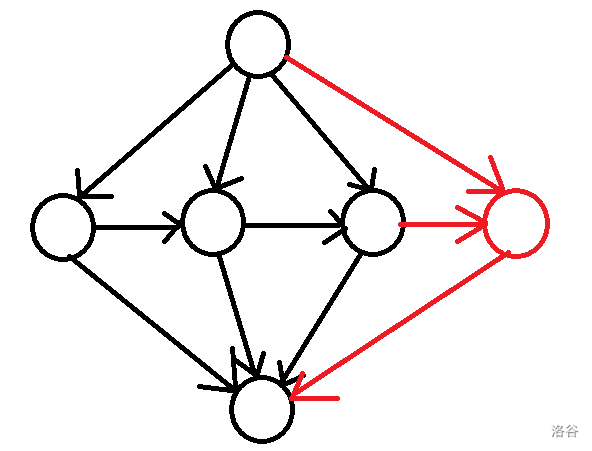
其中源点向每天连流量为 \(1\),费用为 \(-c_i\) 的边,每天向下一天连流量为 \(+\infty\),费用为 \(0\) 的边,每天向汇点连流量为 \(1\),费用为 \(c_i\) 的边。每新加进来一天就会多增加三条边。我们考虑增加了这三条边会对网络产生什么影响。见下图。
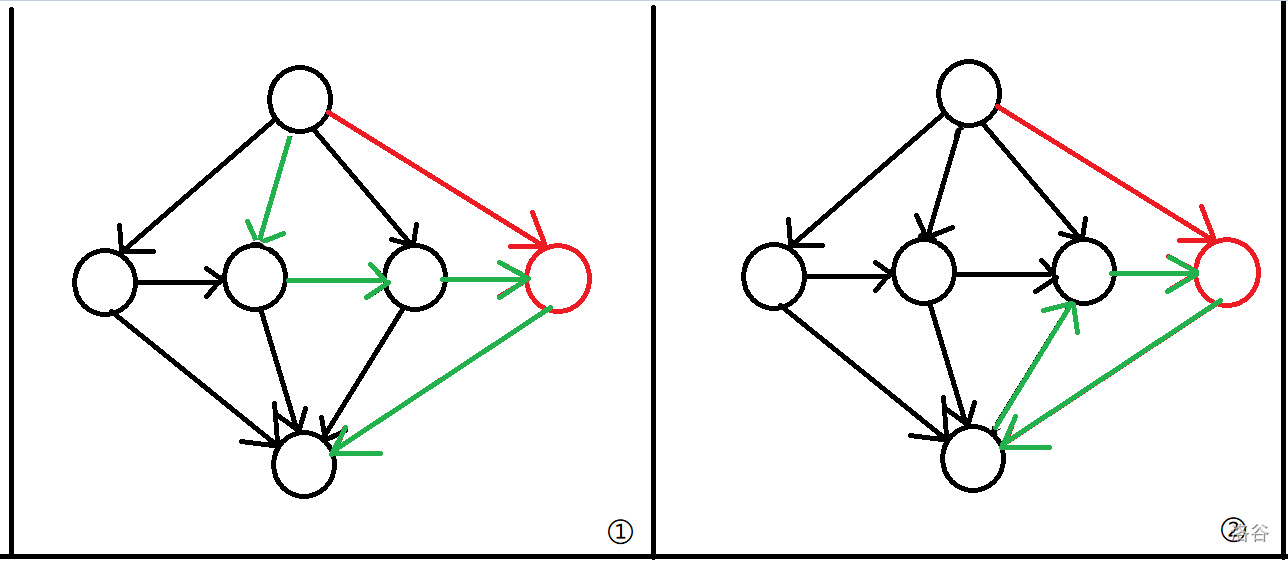
(图二中为将负环消掉,也是费用流中的一个算法)
我们可以发现,新一轮增广只会选择之前没有选择的一天来买股票,或者反悔掉之前卖出的一股股票来现在卖。这样就可以开一个堆维护了。
数据备份
长度为 \(n\) 的序列,要求选 \(k\) 个数,要求这 \(k\) 个数不能相邻,求选出的数最大总和。
数据范围:\(n\le 10^5\)。
本题也是比较经典的模拟费用流例题。我们先把费用流模型建出来,见图一。
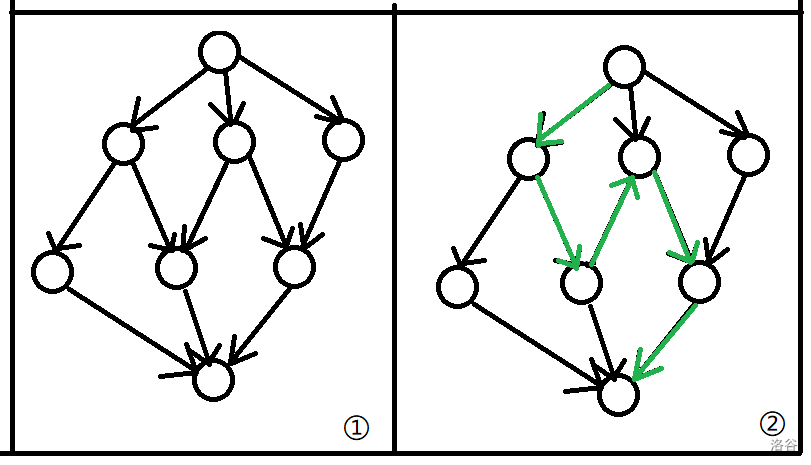
我们这里把数字与数字之间的间隙看作点,把数看作边。我们考虑一次增广的情况,见图二。可以发现,单次增广会把一段区间的状态全部取反,同时这段区间必须满足 0 101...101 0,即两边都不选,并且中间选和不选交替。我们还能发现,这样一次增广后,会把三段区间变为一段区间。用堆和链表维护即可。
我们也可以从贪心的角度来说明这个结论。每次的决策必然是选择最小的,或者是最小值的两边的值。我们可以先选择上最小值,然后删除这三个数,加入值为 \(a_{i-1}+a_{i+1}-a_i\) 的数。这样如果下次再选择到这个数,就代表着我们反悔了。代码和上面的做法完全一样。
另外,由于本题建出了费用流模型,我们可以用 wqs 二分来解决,这里不再说明。
Olympiad in Programming and Sports
有 \(n\) 个学生,每人有两种技能,分别是 \(a,b\) 表示编程能力和运动能力。你需要将他们分为两个团队分别参加编程比赛和体育比赛,编程团队有 \(p\) 人,体育团队有 \(s\) 人,一个学生只能参加其中一项。每个团队的力量是其成员在对应领域能力总和,两个团队的实力和最大是多少。
数据范围:\(n\le 3000\)。
本题依旧可以建出费用流模型。
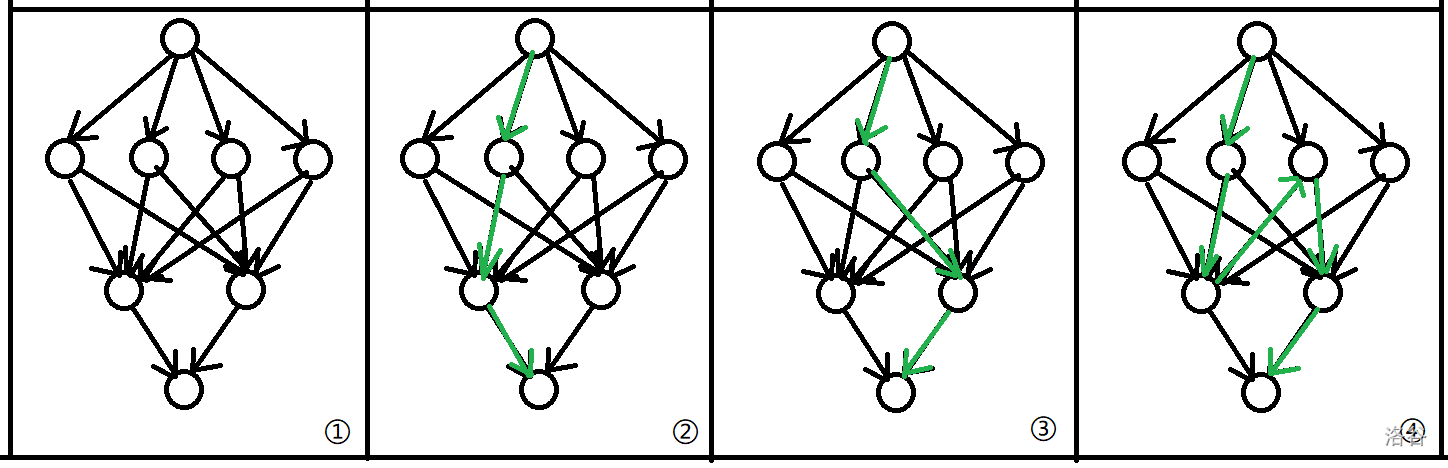
图一即为网络。图二、三、四都为单次增广可能的路径,我们可以选择一个没有被选择的人来让他选择编程或者运动,或者是让它顶替掉一个选择过别的运动的人。我们可以按照这个想出反悔贪心策略:开三个堆来维护 \(a_i, b_i, b_i-a_i\)。一开始先选择编程能力最大的,然后每轮不断取出最大的 \(b_i\) 和最大的 \(a_i+(b_i-a_i)\),重复 \(s\) 轮即可。
Raffles
有 \(n\) 个奖池,第 \(i\) 个奖池有 \(p_i\) 元奖金,已经有 \(l_i\) 张彩票押在上面。现在有 \(t\) 张彩票,你要把这些彩票押到奖金池中,并且在每个奖金池中你押的彩票数不能超过原有的彩票数。如果你在第 \(i\) 个彩票池押了 \(t_i\) 张彩票,你中奖的概率就是 \(\frac{t_i}{t_i+l_i}\),中奖会获得该彩票池的所有奖金。一共有 \(q\) 次事件,每次事件会使一个彩票池中 \(l_i\) 加一或减一。每次事件后输出获得奖金的最大期望值。
数据范围:\(n, q, t\le 2\times 10^5\)。
我们考虑往某个池子里放一个彩票增加的期望钱数。
\[\begin{aligned} \frac{t_i+1}{t_i+1+l_i}-\frac{t_i}{t_i+l_i} &=\frac{(t_i+1)(t_i+l_i)-t_i(t_i+1+l_i)}{(t_i+1+l_i)(t_i+l_i)} \\ &=\frac{l_i}{(t_i+1+l_i)(t_i+l_i)} \end{aligned} \]我们再考虑如果没有修改操作如何求出答案。我们只需要维护两个堆,一个存放当前的决策,一个存放下一次的决策(就比如当前池子里押了 \(x\),下一次决策即为 \(x+1\))。每次拿出下次决策收益最大的,循环 \(t\) 次即可。
当有修改时,我们可以先将其在堆中的信息更新一遍,然后从下一次决策中取出最大的和当前决策进行比较,如果更大就替换。这样复杂度其实是对的,因为我们每次重新跑一遍只会引起一张彩票的变化。
Cardboard Box
\(n\) 个关卡,对每个关卡,你可以花 \(a_i\) 代价得到一颗星,也可以花 \(b_i\) 代价得到两颗星,也可以不玩。问获得 \(w\) 颗星最少代价。
数据范围:\(n\le 3\times 10^5\)。
我们考虑从有 \(i\) 颗星变为 \(i+1\) 颗星的方法:
- 直接选一个之前 \(0\) 颗星的关卡增加一颗星,代价 \(a_i\)。
- 选已经选了一颗星的关卡变为两颗星,代价 \(b_i-a_i\)。
- 让之前一颗星的关卡变为零颗星,一个零颗星的关卡变为两颗星,代价 \(b_i-a_j\)。
- 让之前两颗星的关卡变为一颗星,一个零颗星的关卡变为两颗星,代价 \(b_i-b_j+a_j\)。
我们分类讨论完就可以直接开五个堆分别维护 \(a_i,b_i, -a_i, b_i-a_i, -b_i+a_i\)。每次从上面的决策中选择最大值即可。
序列
给定两个长度为 \(n\) 的正整数序列 \(\{a_i\}\) 与 \(\{b_i\}\),确定两个长度为 \(K\) 的序列 \(\{c_i\}, \{d_i\}\),其中 \(1 \leq c_1 < c_2 < \cdots < c_K \leq n , 1 \leq d_1 < d_2 < \cdots < d_K \leq n\),并要求 \(\{c_1, c_2, \cdots , c_K\} \cap \{d_1, d_2, · · · , d_K\}\geq L\)。目标是最大化 \(\sum^{K}_{i=1} a_{c_i} +\sum^{K}_{i=1} b_{d_i}\)。
数据范围:\(n\le 2\times 10^5\)。
我们建出费用流模型。
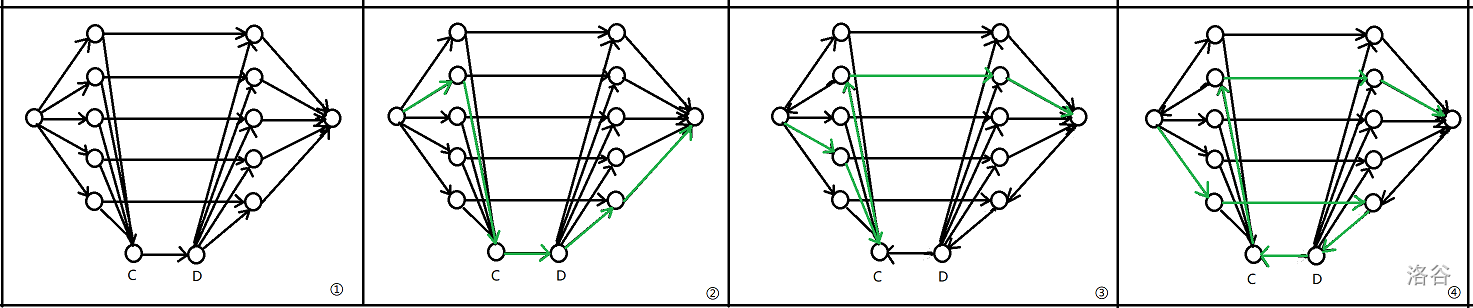
可以发现,只要弧 CD 有流量,那么一定会去选择流它。当弧 CD 没有流量后,我们有如下选择:
- 选择相同下标的数字。
- 找一个可用的左部点和一个左部点被选择的右部点。
- 上面的对称情况。
模拟即可,同时当我们第二或第三种情况后某个点的左部点和右部点都被选择,则可以为弧 CD 增加一点流量。也就是上图中的图四。