图的应用--最小生成树
生成树
概念:所有顶点均由边连接在一起.但不存在回路.
一个图可以有许多不同的生成树.
生成树特点:
- 生成树的顶点个数与图的顶点个数相同.
- 生成树是图的极小联通子图,去掉一条边则非联通
- 一个有n个顶点的连通图的生成树有n-1条边
- 在生成树中再加一条边必然形成回路
- 生成树中任意两个顶点间的路径是唯一的
还有n个顶带n-1条边的图不一定是生成树

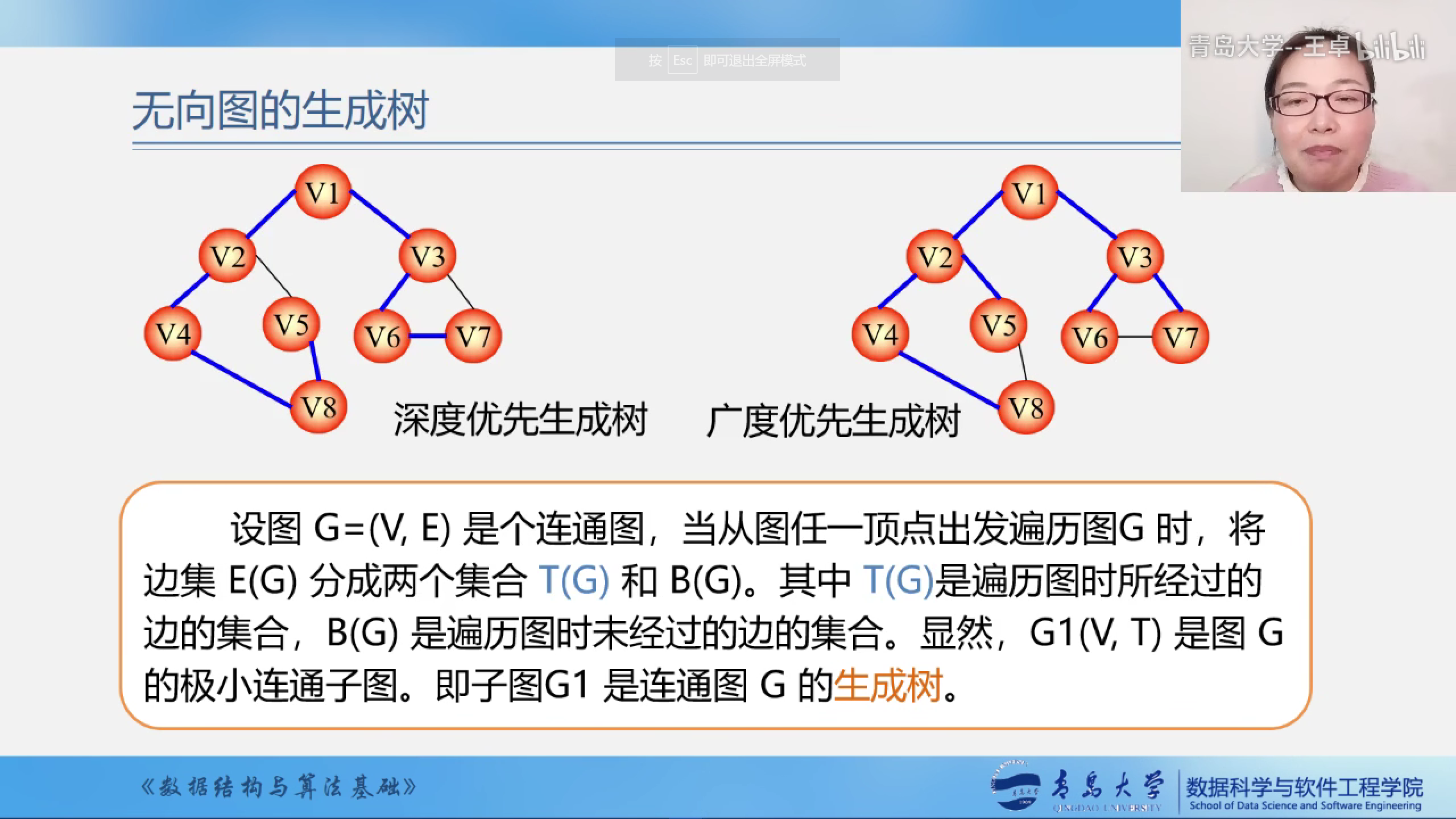
无向图的生成树
使用dfs搜索找到的生成树.叫做深度优先生成树
使用bfs搜索找到的生成树,叫做广度优先生成树.
最小生成树的定义
给定一个无向网络,在该网的所有生成树中,使得各边权值之和最小的那颗生成树成为该网的最小生成树,也叫最小代价生成树.

典型用途

构造最小生成树(MST)

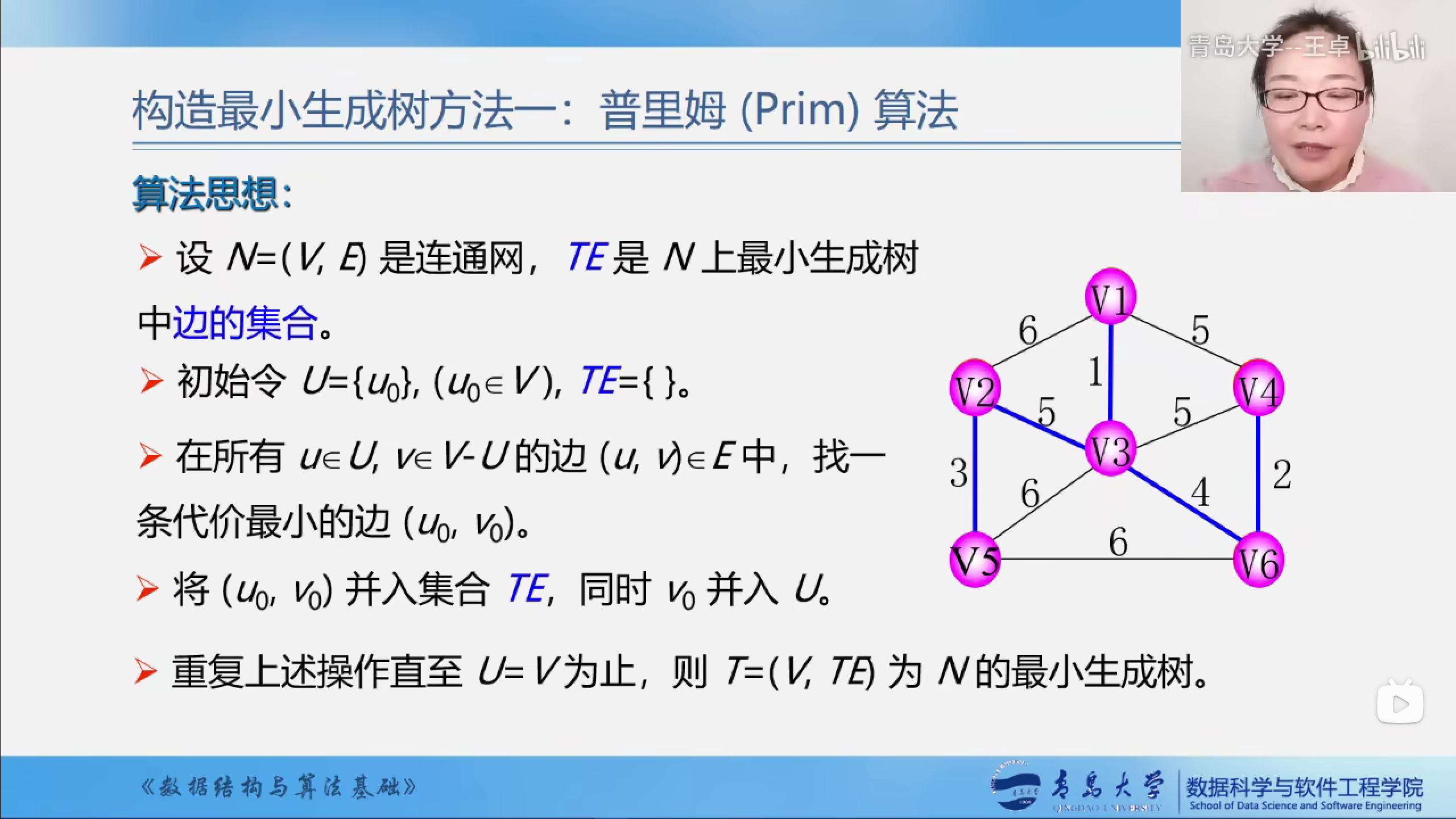
在生成树的构造过程中,图中n个顶点分属两个集合:
- 已落在生成树上的顶点集:U
- 尚未落在生成树上的顶点集:V-U
- 接下来则应在所有连通U中顶点和V-U中顶点的边中选取权值最小的边.

方法1:Prim算法
方法2:Kruskal算法
直接了当的贪心,但是不能形成环.
最小生成树可能不唯一

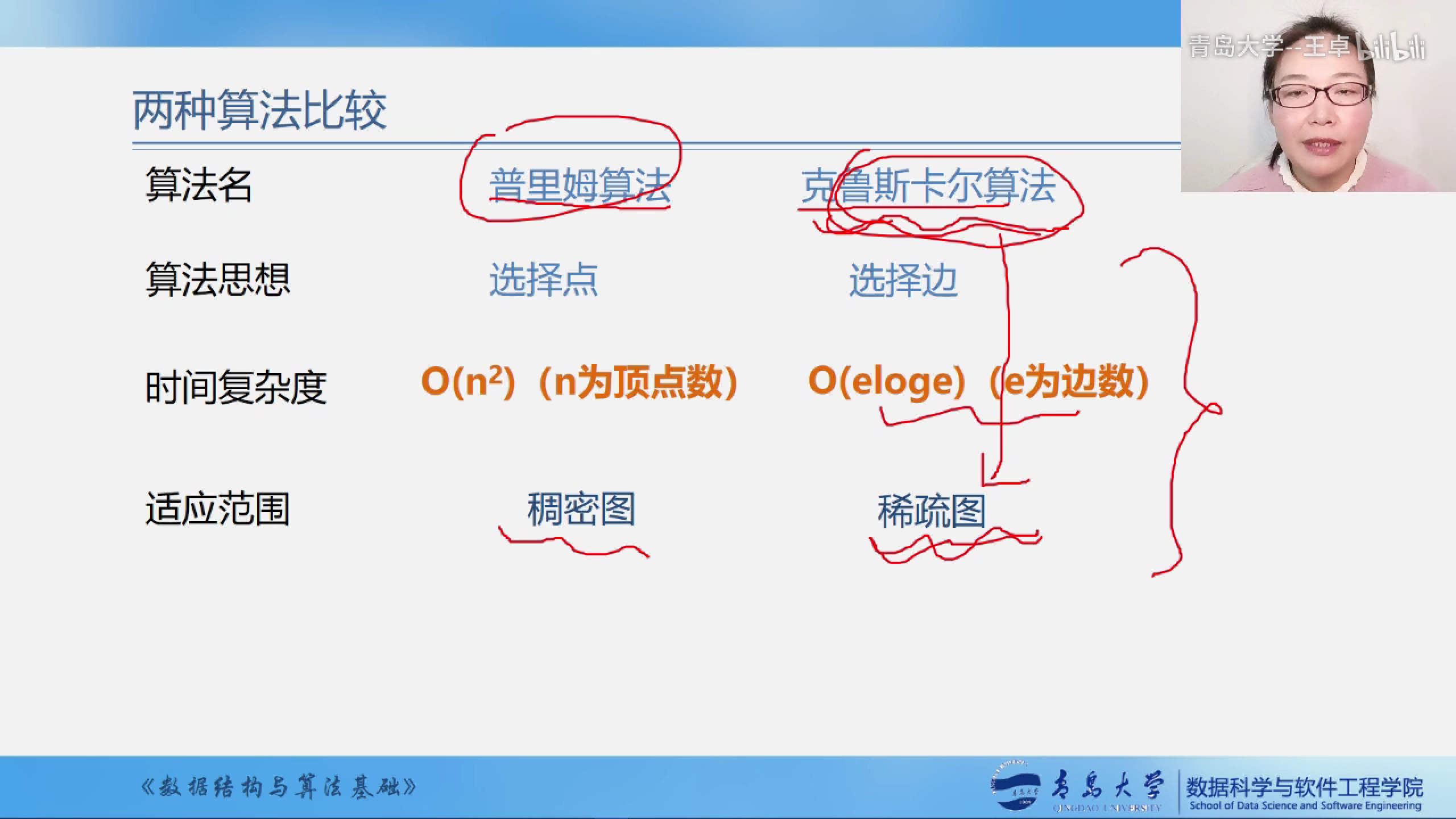
两种算法的比较
P3366 【模板】最小生成树
使用并查集来构建Kruskal算法

#include <bits/stdc++.h>
#define yes cout<<"YES"<<'\n'
#define no cout<<"NO"<<'\n'
using namespace std;
typedef pair<int, int> PII;
const int N = 200008;
struct Node {
int x, y, v;
} a[N];
int fa[50008], n, m;
bool cmp(Node a, Node b) {//自定义排序按照边权的大小进行排序
return a.v < b.v;
}
int findset(int x) {//并查集的findset
if (fa[x] == x) {
return x;
}
int y = findset(fa[x]);
fa[x] = y; //路径压缩
return fa[x];
}
void Kruskal() {
for (int i = 1; i <= n; i++) {
fa[i] = i; //并查集初始化
}
sort(a + 1, a + m + 1, cmp);//排序
int ans = 0;//记录答案
int cnt = n;//现在有几个连通块,初始化的时候有n个
for (int i = 1; i <= m; i++) {
int x = findset(a[i].x);
int y = findset(a[i].y);
if (x != y) {//如果a[i].x和a[i].y不在一个集合里面的话
fa[x] = y;//合并两个集合
ans += a[i].v;//将边权加入到里面
cnt--;//连通块的数量减1
}
if (cnt == 1) {//如果cnt为1就退出循环
break;
}
}
if (cnt == 1) {//打印结果
cout << ans << '\n';
} else {
cout << "orz" << '\n';
}
}
int main () {
cin >> n >> m;
for (int i = 1; i <= m; i++) {
cin >> a[i].x >> a[i].y >> a[i].v;
}
Kruskal();
return 0;
}