一个简单跳转过程的分析
1.源代码如下
#include <stdio.h>
int sub(int d, int e) {
return d - e;
}
int sum(int a, int b) {
int c = sub(100, 9);
return a + b + c;
}
int main(void) {
int a = 12;
int b = 98;
int sum_result = sum(a, b);
return 0;
}
2. 编译后汇编
0x555555555129 <sub> endbr64
0x55555555512d <sub+4> push %rbp
0x55555555512e <sub+5> mov %rsp,%rbp
0x555555555131 <sub+8> mov %edi,-0x4(%rbp)
0x555555555134 <sub+11> mov %esi,-0x8(%rbp)
0x555555555137 <sub+14> mov -0x4(%rbp),%eax
0x55555555513a <sub+17> sub -0x8(%rbp),%eax
0x55555555513d <sub+20> pop %rbp
0x55555555513e <sub+21> retq
0x55555555513f <sum> endbr64
0x555555555143 <sum+4> push %rbp
0x555555555144 <sum+5> mov %rsp,%rbp
0x555555555147 <sum+8> sub $0x18,%rsp
0x55555555514b <sum+12> mov %edi,-0x14(%rbp)
0x55555555514e <sum+15> mov %esi,-0x18(%rbp)
0x555555555151 <sum+18> mov $0x9,%esi
0x555555555156 <sum+23> mov $0x64,%edi
0x55555555515b <sum+28> callq 0x555555555129 <sub>
0x555555555160 <sum+33> mov %eax,-0x4(%rbp)
0x555555555163 <sum+36> mov -0x14(%rbp),%edx
0x555555555166 <sum+39> mov -0x18(%rbp),%eax
0x555555555169 <sum+42> add %eax,%edx
0x55555555516b <sum+44> mov -0x4(%rbp),%eax
0x55555555516e <sum+47> add %edx,%eax
0x555555555170 <sum+49> leaveq
0x555555555171 <sum+50> retq
0x555555555172 <main> endbr64
0x555555555176 <main+4> push %rbp
0x555555555177 <main+5> mov %rsp,%rbp
0x55555555517a <main+8> sub $0x10,%rsp
0x55555555517e <main+12> movl $0xc,-0xc(%rbp)
0x555555555185 <main+19> movl $0x62,-0x8(%rbp)
0x55555555518c <main+26> mov -0x8(%rbp),%edx
0x55555555518f <main+29> mov -0xc(%rbp),%eax
0x555555555192 <main+32> mov %edx,%esi
0x555555555194 <main+34> mov %eax,%edi
0x555555555196 <main+36> callq 0x55555555513f <sum>
0x55555555519b <main+41> mov %eax,-0x4(%rbp)
0x55555555519e <main+44> mov $0x0,%eax
0x5555555551a3 <main+49> leaveq
0x5555555551a4 <main+50> retq
3. 寄存器说明
-
%rsp:栈指针,指向当前函数栈帧的栈顶(最低位置) -
rip: 指向当前正在执行的指令 -
%eax:要返回的值必须存储在%eax中(规定)
4. 指令说明
-
endbr64: 可以忽略,这个指令不会改变任何数据 -
push %rbp: 减小[%rsp],然后将值存入[%rsp][%rsp] = [%rsp] - 8 [%rsp] = [%rbp]注:%rsp中存储的是栈的地址,所以,这里并非将值存入寄存器,而是存储到%rsp所指向的栈地址
-
mov src dest: [dest] = [src] -
movl $0xc,-0xc(%rbp): 将立即数存人栈 -
callq sum: 跳转, 将当前指令的下一条指令地址压栈,之后跳回来继续执行[%rsp] = [%rsp] - 8 [%rsp] = 下一条指令的地址,这里是0x55555555519b [%rip] = 0x55555555513f(sum所在地址,跳转到sum) -
pop %rbp:[%rbp] = [%rsp] [%rsp] = [%rsp] + 8 -
retq:popq %rip: [%rip] = [%rsp] [%rsp] = [%rsp] + 8 -
leaveq:mov %rbp, %rsp popq %rbp
5. 代码说明
假定起始时rsp = X
main()
-
将调用main()的函数的栈帧底存入栈中
push %rbp: %rsp = %rsp-8 = X-8 [%rsp] = [%rbp] -
设置当前函数栈帧的底地址给rbp
mov %rsp,%rbp -
给当前函数创建栈帧,
rsp指向栈帧顶sub $0x10,%rsp rsp = rsp - 16 # 创建一个大小为16B的栈帧 -
接下来四行完成变量的创建,因为不能直接把数字放入寄存器,需要借助栈
-
接下来两行,把变量放入规定的传参寄存器
-
把返回执行地址放入栈中,令rip指向sum,完成跳转
callq 0x55555555513f <sum> [rsp] = [rsp] - 8 [rsp] = 下一条指令的地址,这里是0x5555,5555,519b [rip] = sum所在地址,跳转到sum
此时栈帧
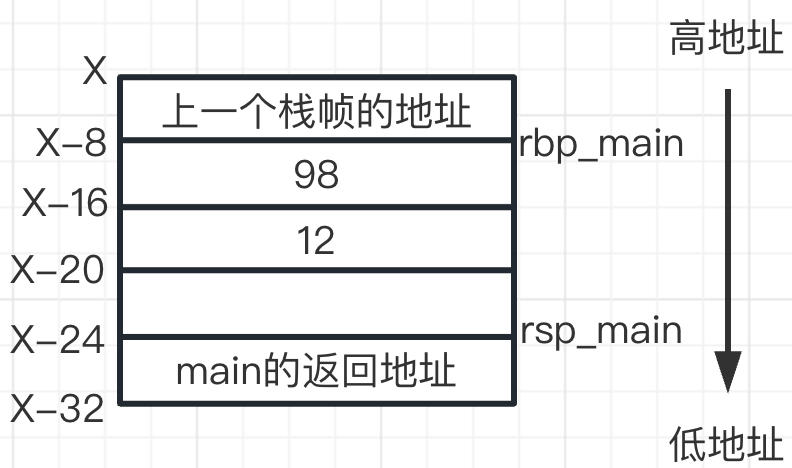
sum()
前面和main函数类似,存储上一个函数的栈帧底,创建栈帧,将上一个函数传过来的参数取出,压入栈中,执行,然后跳到sub函数
此时栈帧
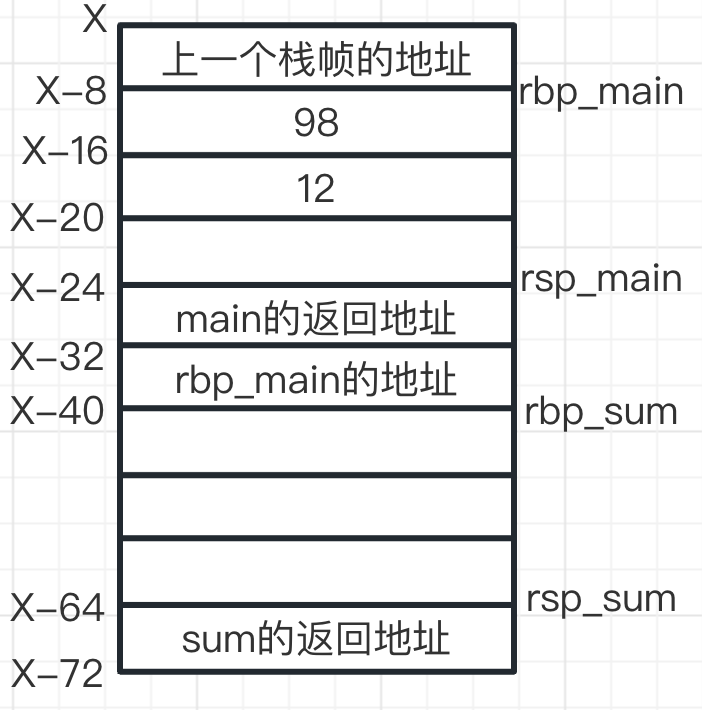
sub()
前面也是类似,从pop %rbp开始介绍
此时栈帧如下
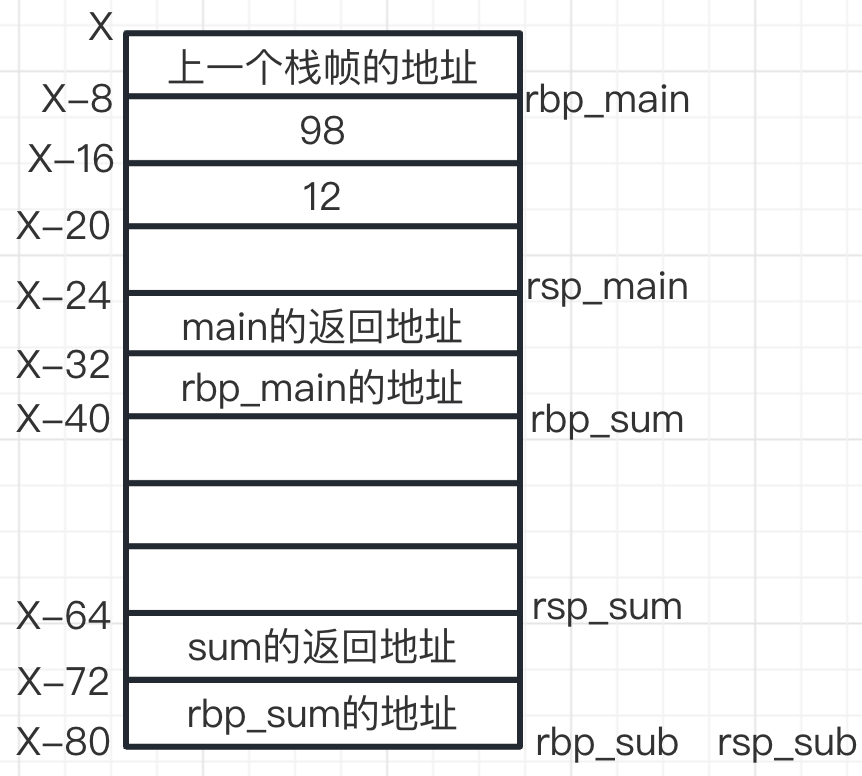
-
pop %rbp[%rbp] = [%rsp] [%rsp] = [%rsp] + 8此时
%rbp指向rbp_sum,%rsp指向sum返回地址 -
retq[%rip] = [%rsp] [%rsp] = [%rsp] + 8此时
rip指向sum返回地址,rsp指向sum函数的栈顶
完成跳回sum()
sum()
因为sub没有创建栈帧,所以返回容易一些,当创建了栈帧时,就需要借助leaveq指令完成返回
-
leaveq1.mov %rbp, %rsp: %rsp = %rbp 2.popq %rbp: [%rbp] = [%rsp] [%rsp] = [%rsp] + 8此时
%rbp指向rbp_main,rsp指向main的返回地址 -
retq[%rip] = [%rsp] [%rsp] = [%rsp] + 8此时
%rip指向main返回地址,%rsp指向sum函数的栈顶
完成跳回main()