简介
红黑树是平衡二叉查找树的一种,前面我们提到,非平衡的 BST,在只有随机插入和查询的情况下,时间复杂度是 $O(\log n)$ 的,然而,如果同时存在随机插入和随机删除,那么时间复杂度会退化到 $O(\sqrt n)$,这是我们无法接受的。
红黑树在插入和删除时,会维持树的平衡,即保证树的高度在 $[\log n, \log(n + 1)]$,理论上极端情况可能树高最大会到达 $2 * \log n$,实际上很难遇到(尽管这样,还是保证了 $O(\log n)$ 的增删查改时间复杂度。
红黑树其实是 2-3 查找树或者 2-3-4 查找树的一种二叉树的实现方式。其中基于 2-3 树实现的红黑树被称为左倾红黑树(Left-Leaning Red-Black Trees, LLRB),基于 2-3-4 树实现的就是普通的红黑树,左倾红黑树实现起来比红黑树更简单一些(《算法 第四版》里面也主要讲的左倾红黑树),因此先讲左倾红黑树。
2-3 查找树
在普通的二叉树中,非叶子结点可以有一个或者两个子结点,如果没有子结点,那么就是叶子结点。
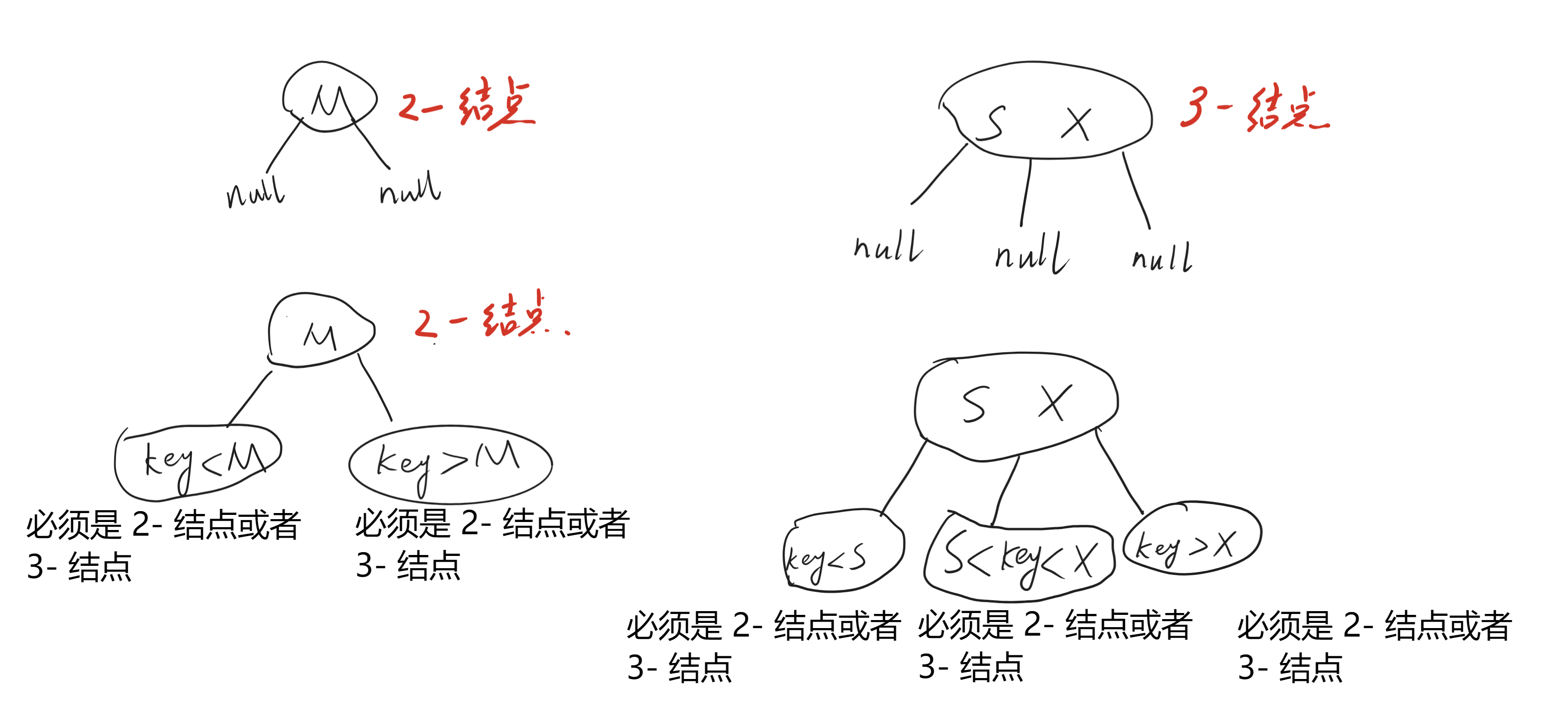
而 2-3 查找树的限制要严格很多。我们将拥有一个 key 和两个链接 的结点称为 2- 结点,拥有两个 key 和三个链接的结点称为 3- 结点。
- 2- 结点含有一个 key,两个 link;
- 3- 结点含有两个不同的 key,三个 link。
3- 结点含有两个 key($key_1 < key_2$),三个链接,左链接指向 2-3 树中的 key 都小于 $key_1$,中间链接指向的 2-3 树中的 key 都满足 $key_1 < key < key_2$,右链接指向的 2-3 树中的 key 都大于 $key_2$。
2-3 查找树只能由 2- 结点或者 3- 结点组成(这里不统计空结点(null)),可以看到 2-3 查找树的限制是非常严格的,这也让它可以拥有一些非常理想的性质。
一颗完美平衡的 2-3 查找树中所有空结点(null)到根结点的距离都应该是相同的,后续我们都使用 2-3 树指代一颗完美平衡的 2-3 查找树。(其他情况下表示的可能是一种更一般的结构)。
查找
将二叉查找树的查找算法一般化就能得到 2-3 树的查找算法。
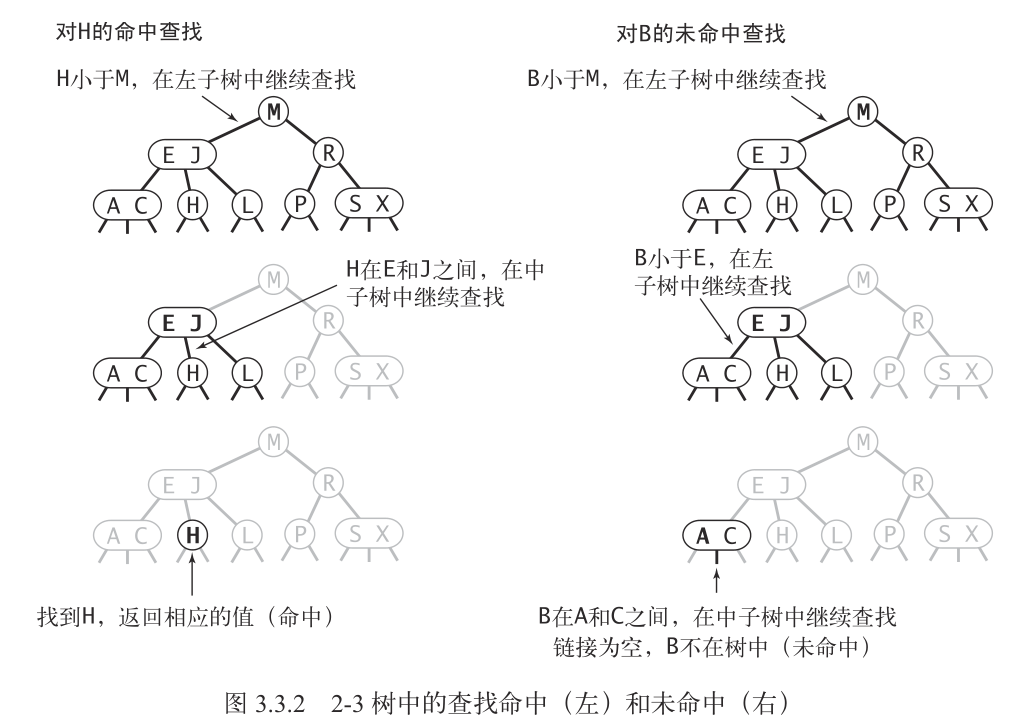
向 2- 结点中插入新 key
首先进行一次未命中的查找,如果未命中的查找结束于一个 2- 结点,那么我们往这个 2- 结点中插入新的 key,使这个 2- 结点变成 3- 结点就好了,不影响所有结点的树高。
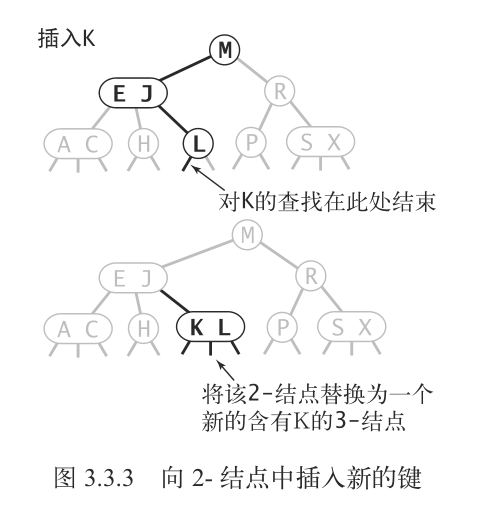
插入 key 时,由于 2-3 树的性质,我们必定是在叶子结点处执行插入。
向 3- 结点中插入新的 key
1. 向一个只含有一个 3- 结点的树中插入新 key
先组成一个临时的 4- 结点,然后将 4- 结点中的三个 key 中间的 key 上移作为剩下的 3- 结点的父结点。如下图所示:
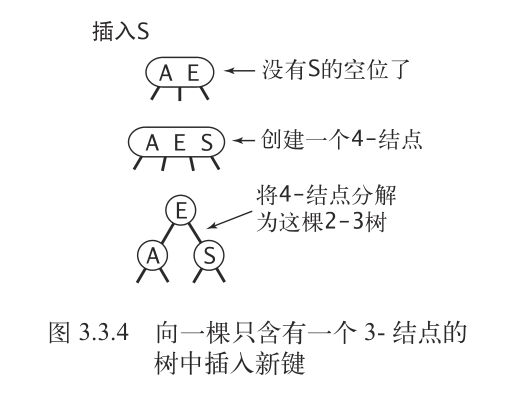
注意到,这样操作之后,2-3 树的高度 $+1$ 了,所有原来位置的结点高度均 $+1$。
2. 向一个父结点为 2- 结点的 3- 结点中插入新 key
还是先组成一个临时的 4- 结点,然后将 4- 结点的三个 key 中中间的 key 上移,将这个 key 插入到本来为 2-结点的父结点组成 3- 结点,树的高度不变,如下图所示:
3. 向一个父结点为 3- 结点的 3- 结点中插入新 key
还是先组成一个临时的 4- 结点,然后将 4- 结点的三个 key 中中间的 key 上移,即将这个 key 插入到父结点中:此时情形就可以转化成 $1$ 或者 $2$ 或者 $3$。
如果转换成 $3$,那么就相当于是递归操作。
因此,对于 $3$ 这一插入类型,我们可以从递归的角度去理解它,递归终止条件就是切换到情形 $1$ 或者 $2$,每次递归中执行的操作就是构成一个临时的 4- 结点,然后将 4- 结点的三个 key 中中间的 key 上移,插入到父结点中。
如下图所示:
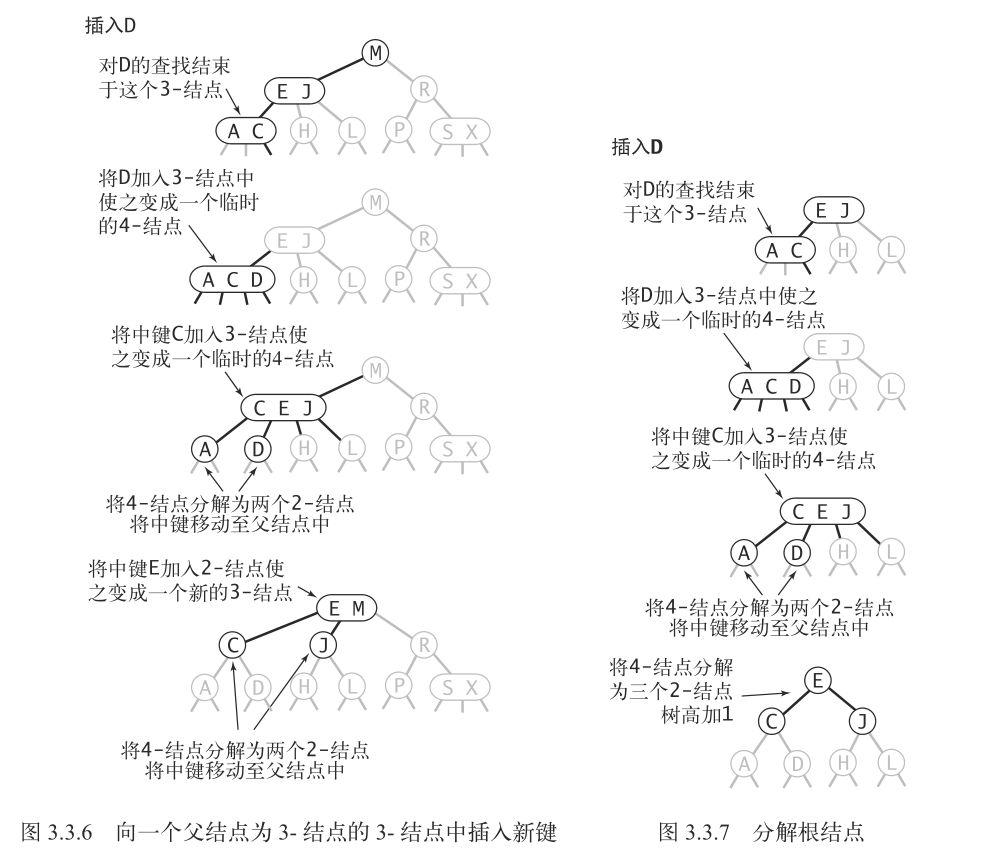
从插入操作我们可以分析得出,对 2-3 树来说,插入操作不会破坏它的完美平衡!要么整棵树的高度不变,要么整颗树的高度 $+1$,因此,根结点到所有 null 结点的长度依旧是相同的。
2-3 树的树高介于 $\log n$ 和 $\log_3 n$ 之间。
删除结点
待会再自己写,《算法 第四版》上并没有写。。。
总结
直接实现 2-3 树比较复杂,执行插入、删除操作时要维护和变换的信息比较多,可能性能还不如普通的二叉查找树。
尽管我们可以用不同的数据类型表示 2- 结点和 3- 结点并写出变换所需的代码,但用这种直白的表示方法实现大多数的操作并不方便,因为需要处理的情况实在太多。我们需要维护两种不同类型的结点,将被查找的键和结点中的每个键进行比较,将链接和其他信息从一种结点复制到另一种结点,将结点从一种数据类型转换到另一种数据类型,等等。实现这些不仅需要大量的代码,而且它们所产生的额外开销可能会使算法比标准的二叉查找树更慢。
左倾红黑树(LLRB)
红黑树的基本思想是用标准的二叉查找树(结点都是 2- 结点),以及一些额外的信息(用来替换 3- 结点)来表示 2-3 树。
我们将树中的 link 分为两类,一类是 red link 将两个 2- 结点连接起来,就构成了一个 3- 结点,合法的 LLRB 要求只有父结点和左子结点之间的 link 才能是红色的;另一类是 black link 将两个 2- 结点连接起来,对应 2-3 树中的普通 link。
准确说,我们将 3- 结点表示为由一个左斜的 red link 相连的两个 2- 结点,如所示,我们可以直接使用标准 BST 的 get 方法。
LLRB 的另一种定义是含有 red 和 black link 并且满足下列条件的二叉查找树:
- red link 均为左斜 link;
- 没有一个结点同时和两条 red link 相连;
- 该树是完美黑色平衡的,即任意 null 结点到根结点的路径上的 black link 数量相同。
如果我们将一颗 LLRB 中的 red link 画平,那么所有 null 结点到根结点的距离都将是相同的。
由于每个结点都只有一个父结点,因此对每个结点来说,从它的父结点到它自身的 link 是唯一的,因此我们可以将 link 的颜色保存再表示结点的类 Node 的布尔成员变量 color 中。我们规定 null link 是黑色的
const bool kRed = true;
const bool kBlack = false;
class Node {
private:
int key_;
int val_;
int cnt_;
bool color_;
Node *left_;
Node *right_;
public:
Node(int key, int val, int cnt, bool color) :
key_(key), val_(val), cnt_(cnt), color_(color), left_(nullptr), right_(nullptr) {
}
private:
bool isRed(Node *x) {
if (x == nullptr) {
return false;
}
return x->color_ == kRed;
}
};