最近写了一段时间的网络流,现在应该总结一下了。
网络流就是将原问题抽象成包含顶点和边有容量限制的网络。
本文中有些题目的题解复制自网络,仅作个人学习总结之用。
1.最大流
最大流可以看作使用 flow 来做出一系列的限制,从而满足原题条件。
1.1 拆点
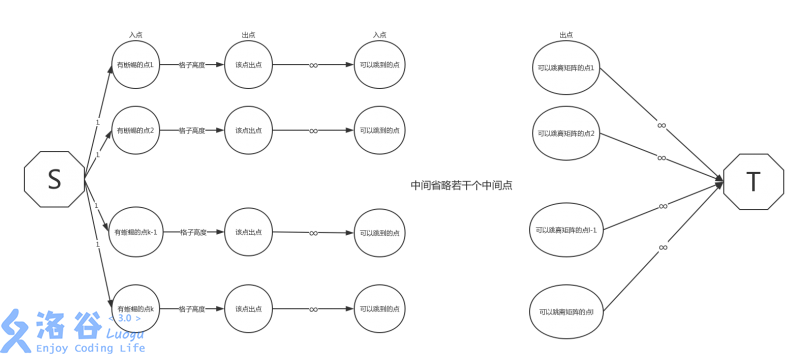
有时候某一个点还有额外的限制,这个时候就需要把一个点拆成两个点,用它们之间的边来描述限制。
LG2472 [SCOI2007] 蜥蜴
将整个网格地图看作一个网络,,某一个节点拆成两个点(称为左端点和右端点),之间连一条边表示跳的青蛙的限制数。相互之间如果可以通达就从右一端点向左一端点连边。s 向所有有青蛙的左端点连一条容量为青蛙数的边。能通达外部右端点向 t 连一条容量为 inf 的边。
1.2 分层图网络流
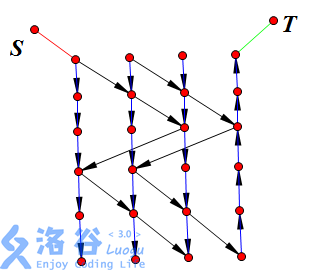
基于时间等因素,网络状态有所改变,这时候就需要构建分层图。
LG2754 [CTSC1999] 星际转移问题
注意到每个太空船的位置在随时间的改变而改变。
基于时间构建分层图。
首先判断无解,即地球和月球没有被太空船联通(并查集判断)。
我们将所有空间站+地球+月球称为一层节点。
接着枚举时间,每一新时刻构建一层节点,根据太空船的位置关系从上一层节点向这一层节点连边,容量限制为太空船的载客量,直到最大流大于等于地球人数 k。
由于 dinic 残量网络的性质,我们可以每次在残量网络上跑 dinic,将新增的流直接加到最大流上,因此时间上远远小于跑 t 遍 dinic 的理论复杂度。
LG2766 最长不下降子序列问题
[问题分析]
第一问时LIS,动态规划求解,第二问和第三问用网络最大流解决。
[建模方法]
首先动态规划求出 F[i],表示以第 i 位为开头的最长上升序列的长度,求出最长上升序列长度 K。
1、把序列每位 i 拆成两个点 <i.a> 和 <i.b> ,从 <i.a> 到 <i.b> 连接一条容量为1的有向边。
2、建立附加源 S 和汇 T ,如果序列第 i 位有 \(F_i=K\),从 S 到 <i.a> 连接一条容量为1的有向边。
3、如果 \(F_i=1\),从 <i.b> 到 T 连接一条容量为 1 的有向边。
4、如果 \(j>i\) 且 \(A_i < A_j\) 且 \(F_j+1=F_i\) ,从 <i.b> 到 <j.a> 连接一条容量为1的有向边。
求网络最大流,就是第二问的结果。把边 (<1.a>,<1.b>),(<N.a>,<N.b>),(S,<1.a>),(<N.b>,T) 这四条边的容量修改为无穷大,再求一次网络最大流,就是第三问结果。
[建模分析]
上述建模方法是应用了一种分层图的思想,把图每个顶点 i 按照 F[i] 的不同分为了若干层,这样图中从S出发到T的任何一条路径都是一个满足条件的最长上升子序列。
由于序列中每个点要不可重复地取出,需要把每个点拆分成两个点。单位网络的最大流就是增广路的条数,所以最大流量就是第二问结果。
第三问特殊地要求 x1 和 xn 可以重复使用,只需取消这两个点相关边的流量限制,求网络最大流即可。
1.3 二分图匹配
根据二分图匹配的性质,可以使用网络最大流求解。
同时二分图多重匹配可以使用网络最大流求解,二分图带权最大匹配可以使用最小费用最大流求解。
这一类题型的难点一般在于二分图的建模,而不是网络流模板的使用。
1.4 最小路径点覆盖
最小路径点覆盖问题指的是在一个有向图中,找出最少的路径,使得这些路径经过了所有的点。
构建模型,定义原有向图为 G,新图为 G2。
将 G 拆点,分为左部点和右部点,令 G 中节点 x 的左部点为 l(x),右部点为 r(x)。若 G 有边 (x,y),那么连边 l(x) 与 r(y)。这样作出的二分图就是 G2。
G 的最小路径覆盖 = n - G2 的最大匹配
LG2765 魔术球问题
两个能构成完全平方数的数之间小数向大数有边,不断加入新数,直到最小路径点覆盖 > 柱子数 n。最终答案就是加入的数的个数减一。
还有就是要输出路径,根据网络流的性质,一条边满流了就说明两点之间应该是同一根柱子的相邻关系,枚举一下边最后按照上述关系输出即可。