一. 栈

1. 栈的概念

栈 (stack) 是一种操作受限的线性表，栈的操作被限定在线性表的尾部进行，栈结构有两个特殊概念：

• 栈顶：栈的尾部被称为栈顶(Top)；
• 栈底：另一端固定不动，被称为栈底(Bottom)。

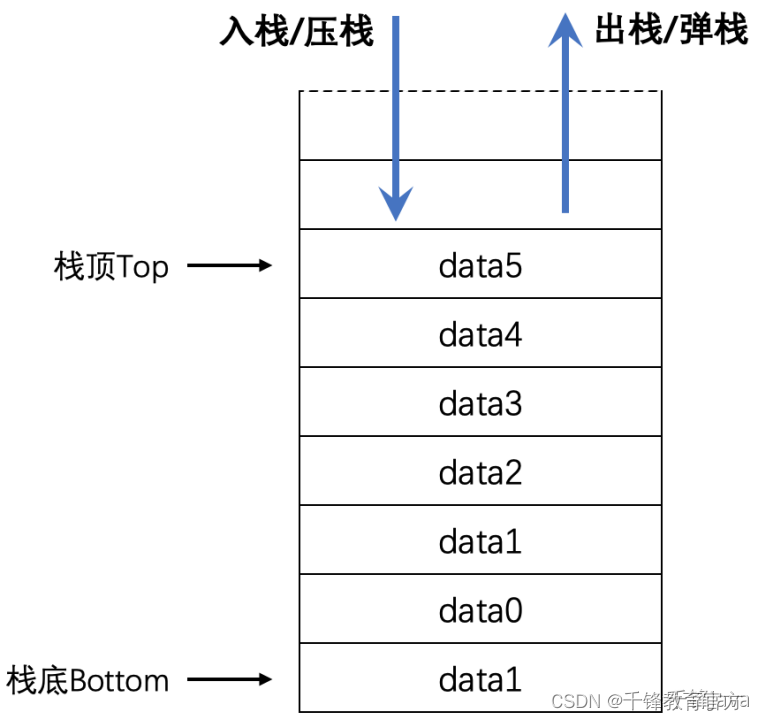
栈中的元素只能先入后出。 最早进入栈的元素所在的位置是栈底，最后进入栈的元素所在的位置是栈顶。数据进入栈的过程叫入栈或压栈，数据从栈中出去的过程叫出栈或弹栈。 如下图所示：

2. 栈的实现

在实现上，栈既可以用数组来实现，也可以用链表来实现。用数组实现的栈叫顺序栈或静态栈，用链表实现的栈叫做链式栈或动态栈，这两种实现方式分别如下图所示：

3. 栈的操作

刚刚给大家介绍了栈顶和栈底的概念，栈的操作就和这两个概念有关。栈一般只有两个操作：入栈和出栈。

3.1 入栈

入栈操作就是把元素(数据)放入到栈中，入栈操作又称压栈，有时也称之为push操作，均表示入栈操作含义。需要注意的是，根据栈结构的特点，入栈只允许从栈顶放入元素，进入栈的新元素会在最上方，成为栈顶。

对于入栈操作的时间复杂度，因为只涉及到一个元素的操作，因此非常简单为O(1)。

3.2 出栈

出栈操作就是把元素（数据）从栈中取出，出栈操作又称弹栈，有时也称之为pop操作，均表示出栈操作含义。同样需要注意，根据栈结构的特点，出栈只需要从栈顶取出元素，元素出栈后，原次顶元素会成为新的栈顶元素。

出栈操作的时间复杂度与入栈操作的时间复杂度相同，均是操作栈顶一个元素，因此出栈操作时间复杂度为O(1)。

4. 栈的特点

如上图所示，清晰的展示了栈的入栈操作和出栈操作。可以看到，无论入栈操作，还是出栈操作，都是操作的栈顶元素。

由此，给大家总结栈结构的特点：后进先出，即后进入的元素会先出栈。在计算机术语中，后进先出描述为Last In First Out，简称LIFO；另外也有人表述为先进后出(Frist In Last Out，简称FILO) ，这两者含义其实是相同的。

5. 栈的应用

在实际的应用实践中，我们可以利用栈结构的特殊性和其特点，解决某些特定的问题，此处给大家介绍常见的几个

5.1 子程序调用

程序在执行过程中，不免会涉及到调用。利用栈结构，可以在跳往子程序前，先将下个指令的地址存到堆栈中，直到子程序执行完后再将地址取出，以便回到原来的程序中。

5.2 浏览器前进和后退

我们使用两个栈X和Y，把首次浏览的页面依次压入栈X，当单击后退按钮时，再依次从栈X中出栈，并将出栈的数据依次放入栈Y。当单击前进按钮时，我们依次从栈Y中取出数据， 放入栈X中。当栈X中没有数据时，说明没有页面可以继续后退浏览了。当栈Y中没有数据，那就说明没有页面可以单击前进按钮浏览了。

5.3 表达式求值

首先大家要知道什么是表达式，以及有哪些表达式，才能进一步学习如何进行表达式求值。根据百科的定义：表达式是由数字、算符、数字分组符号(括号)、自由变量和约束变量等以能求得数值的有意义排列方法所得的组合。

听起来非常的抽象和不好理解，我们可以简单地说：由一个或多个操作数通过操作符组合而成的式子就是表达式。

比如：3+5、a-b、c==d等这些都是表达式，在这三个表达式中，均包含两个操作数和一个操作符。编程中常见和使用的表达式有：算术表达式、逻辑表达式、字符串表达式等。

表达式按照操作数和操作符顺序的不同，又可以分为三种为：中缀表达式、前缀表达式、后缀表达式。

• 中缀表达式：中缀表达式是一个通用的算术或逻辑公式表示方法，我们从小学就接触的算术表达式就是中缀表达式的写法。比如a + b 就默认是中缀表达式。中缀表达式对大家来说很熟悉，但是对计算机来说比较难计算。因为要比较运算符的优先级，所以一般将中缀表达式转化为后缀表达式再进行表达式的运算。
• 前缀表达式：前缀表达式是一种没有括号的算术表达式，与中缀表达式不同的是，其将运算符写在前面，操作数写在后面。为纪念其发明者波兰数学家卢卡西维茨(Jan Lukasiewicz)，前缀表达式也称为“波兰表达式”。例如，- 1 + 2 3，它等价于1-(2+3)。
• 后缀表达式：后缀表达式将运算符写在操作数之后。也叫做逆波兰表达式(Reverse Polish notation，RPN，或逆波兰记法)。

在本文中，我们以后缀表达式求值为例，向大家介绍如何利用栈结构计算表达式的值。

首先，我们需要学习后缀表达式运算求值的规则，其运算思路是：从左至右扫描后缀表达式，遇到数字时，将数字压入栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做出相应的计算，并将结果入栈。重复上述过程，直到表达式的最右端。最后运算得出的值即为表达式的计算结果。

文字描述太过抽象，我们通过具体例子进行说明。例如：求后缀表达式3 4 + 5 * 6 -的值，步骤如下：

(1). 从左向右扫描表达式，首先遇到数字，将数字3和数字4压栈。(此时栈中有2个元素为：3、4)

(2). 继续向右扫描，遇到+运算符。弹出4和3(4为栈顶元素，3为次顶元素)，计算4+3=7，将结果7压入栈中。(此时，栈中只有1个元素：7)

(3). 向右继续扫描，遇到数字5，将数字5压入栈中。(此时，栈中包含2个元素：7、5)

(4). 向右扫描，遇到号运算符，弹出栈顶元素5和次栈顶元素7，并计算75=35，将结果35压入栈中。(此时，栈中只有1个元素：35)

(5). 向右扫描，遇到数字6，将数字6压入栈中。(此时，栈中包含2个元素：35，6)

(6). 向右扫描，遇到-运算符，弹出栈顶元素6和次栈顶元素35，并计算35-6=29，将数字29压入栈中。(此时，栈中只有1个元素：29)

(7). 整个表达式扫描结束，取出栈中的元素29，就是最后表达式的结果。

二. 队列

1. 队列的概念

队列 (Queue) 也是一种操作受限的线性表，是先进先出的线性表。队列的出口端叫作队头(front)，队列的入口端叫作队尾(rear)。队列只允许在队尾进行添加操作，在队头进行删除操作。队列的操作方式和栈类似，唯一的区别在于队列只允许新数据在队尾进行添加，如下图所示：

队列是Java中常用的数据结构，队列的存储结构有两种：一种是基于数组实现的；另一种是基于单链表实现的。

用数组实现队列时，为了入队操作的方便，把队尾位置规定为最后入队元素的下一个位置。 用数组实现的队列叫作顺序队列。数组实现的队列在创建的时候就已经确定了数组的长度，所以队列的长度是固定的，但是可以循环使用数组，所以这种队列也称之为循环队列。

用链表实现的队列叫作链式队列。链表实现的队列内部通过指针指向形成一个队列，这种队列是单向的且长度不固定，所以也称之为非循环队列。

2. 队列的特点

如上图所示，所有的元素都是从队尾进入队列，若需要出队，则从另外一端对头取出元素。我们会发现，元素从队列中出队的顺序刚好是元素进入队列的顺序。我们把这种进入和出来的顺序相同的队列的特点，称之为先进先出(First In First Out，简称为FIFO) 。

3. 队列的操作

同栈类似，队列也是一种操作受限，队列有入队和出队两种操作。接下来，我们详细介绍：

3.1 入队

入队又称enqueue，入队就是把新元素放入队列中，只允许在队尾的位置放入元素，新元素的下一个位置将会成为新的队尾。添加数据时，首先判断队列的长度是否超出了数组的长度，如果超出则就添加失败(也可以设置成等待，等队列里的数据出队，然后再添加进去)。元素入队完成后，队列长度加一，rear指针也会相应自增一。如下图所示：

3.2 出队

出队又称dequeue，出队就是把元素移出队列，只允许在队头一侧移出元素，出队元素的后一个元素将会成为新的队头。元素出队后，队列的长度减一，front指针自增一。如下图所示：

4. 时间复杂度

无论是顺序队列还是链式队列，入队和出队操作都只涉及1个元素的操作，因此队列操作的时间复杂度都是O(1)。队列的主要应用于资源池、消息队列、命令队列等。

三. 串

1. 概念

我们通常将字符串简称为串，其是由零个或多个字符组成的有限序列。串可以是字母、数字或其他字符。串中的字符数目称为串的长度，零个字符的串称为空串，它的长度为0。

串中任意个连续字符组成的子序列称为该串的子串，包含子串的串称为主串。通常我们把字符在序列中的序号为该字符在串中的位置，子串在主串中的位置则以子串的第一个字符在主串中的位置来表示。当两个串的长度相等，并且各个对应的字符都相等时，称两个串相等。由一个或多个空格组成的串称为空格串。空格穿并非空串，它有长度，它的长度为串中空格符号的个数。

2. 串的特性

由此，我们可以得知串的几个结论：

• 串是由零个或多个字符组成的有限序列；
• 串可以由字母、数字或其他字符组成；
• 串中的字符数目称为串的长度；
• 零个字符的串称为空串，它的长度为0；
• 串中任意个连续的字符组成的子序列，称为该串的子串；
• 由一个或多个空格组成的串称为空格串；
• 空格穿并非空串，它有长度，它的长度为串中空格符号的个数。

以上这些简洁的结论，在面试题中可能会遇到，大家需要注意一下。 关于串的其他操作，我们在后面学习算法时，会单独组织一篇内容进行介绍，此处不再赘述。

四. 结语

本篇文章中，向大家介绍了栈、队列和串三种新的线性数据结构。这三种数据结构相对数组和链表而言，操作比较简单，也比较容易理解，各位在学习时需要记住这几个不同数据结构特有的特点。在时间复杂度分析这个指标上，栈和队列的操作均为O(1)。