分治算法
概述
分而治之 ,称之 分治 。 本质 就是将一个大规模的问题分解为若干 规模较小 的 相同子问题 ,分而治之。
本质
可以使用分治算法的情况——问题需要满足一下三个条件:
-
原问题可被分解为若干规模较小的相同子问题;
-
子问题 相互独立 ;
-
子问题的解可以 合并 为原问题的解。
分治算法 求解方法 如下。
-
分解 :将原问题分解为若干规模较小、相互独立且与原问题形式相同的子问题。
-
治理 :求解各个子问题。由于各个子问题与原问题形式相同,只是规模较小,所以当子问题划分得足够小时,就可以用较简单的方法解决。
-
合并 :按原问题的要求,将子问题的解组曾合并形成原问题的解。
一言以蔽之,分治算法是将一个难以直接解决的大问题分割成一些规模较小的相同问题,以便各个击破、分而治之。在分治算法中,各个子问题形式相同,解决方法也一样,因此可以使用递归算法快速解决。
合并排序
在数列中,如果只有一个数,那么它本身就是有序的;如果只有两个数,那么进行一次比较就可以完成一次排序。也就是说, 数越少,排序越容易。 那么,对于一个由大量数据组成的数列,我们很难一次完成排序,这时可将其 分解 为小的数列,一直分解到只剩一个数时,本身已有序,再把这些有序的数列合并在一起,执行一个 和分解相反 的过程,从而完成对整个序列的排序。
合并排序就是采用 分治 策略,将一个大问题 分成 很多个小问题, 先解决小问题,再通过小问题解决大问题 。由于排序问题给定的是一个无序序列,所以可以把待排序元素 分解 成两个规模大致相等的子序列,如果不易解决,则再将得到的子序列 继续分解 ,直到在子序列中包含的元素个数为 1 .因为单个元素的序列本身是有序的,此时便可以进行合并,从而得到一个完整的有序序列。
-
算法设计
合并排序是采用 分治策略 进行 排序 的算法,是分治算法的一个典型应用和完美体现。它是一种 平衡、简单的 二分 分治策略。
算法步骤如下。- 分解: 将待排序元素分成大小大致相同的 两个子序列 。
- 治理: 对两个子序列进行 合并排序 。
- 合并: 将 排好序 的有序子序列进行合并,得到最终的 有序序列 。
-
图解
给定一个数列 \((42,15,20,6,8,38,50,12)\) ,执行合并排序的过程如下图所示。
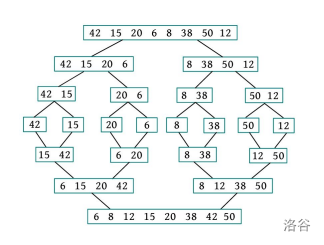
从上图可以看出,首先将待排序元素分成大小大致相同的 两个子序列 ,然后把子序列分成大小大致相同的 两个子序列 ,如此下去,直到分解成 一个元素 时为止,这时含有一个元素的子序列就是 有序的 ;然后 执行合并 操作,将两个有序的子序列 合并为一个 有序序列,如此下去,直到 所有的 元素都合并为一个有序序列时为止。
-
算法设计
-
合并操作
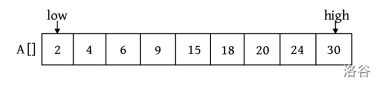
为了进行合并,这里引用一个 辅助合并函数 Merge(A,low,mid,high) ,该函数将排好序的两个子序列 A[low:mid] 和 A[mid+1:high] 进行排序。其中, low、high 代表带合并的两个子序列在数组中的 下界 和 上界 , mid 代表下界和上界的 中间位置 ,如下图所示。
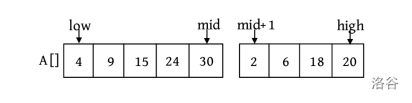
这里还设置3个工作指针 \(i 、j 、k\) (整型下标)和一个辅助数组B。其中, \(i\) 和 \(j\) 分别指向 两个 待排序 子序列 中 当前待比较的元素 , \(k\) 指向 辅助数组B 中 待放置元素 的位置。比较 A[ \(i\) ] 和 A[ \(j\) ] ,将较小的赋值给 B[ \(k\) ] ,相应的指针同时向后移动。如此反复,直到所有元素都处理完毕。最后把辅助数组B中排好序的元素 复制 到数组A中,如下图所示。
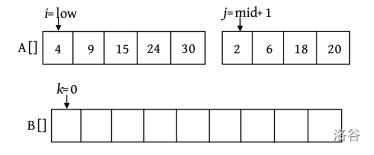
第1次比较时,\(A[i]=4,A[j]=2\) ,将较小的元素2放入数组B中, \(j\) ++, \(k\) ++ 。
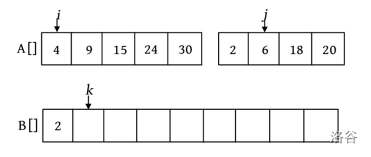
第2次比较时, \(A[i]=4,A[j]=6\) ,将较小的元素4放入数组B中, \(i\) ++, \(k\) ++ 。
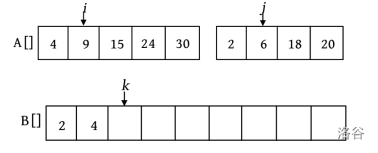
第3次比较时, \(A[i]=9,A[j]=6\) ,将较小的元素6放入数组B中, \(j\) ++, \(k\) ++ 。
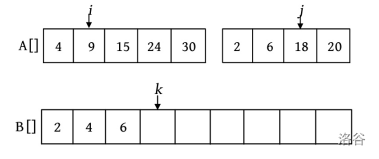
第4次比较时, \(A[i]=9,A[j]=18\) ,将较小的元素9放入数组B中, \(i\) ++, \(k\) ++ 。
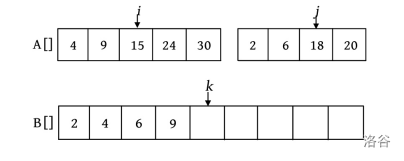
第5次比较时, \(A[i]=15,A[j]=18\) ,将较小的元素15放入数组B中, \(i\) ++, \(k\) ++ 。
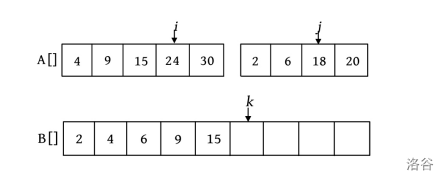
第6次比较时, \(A[i]=24,A[j]=18\) ,将较小的元素18放入数组B中, \(j\) ++, \(k\) ++ 。
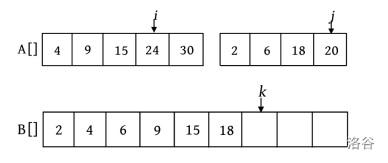
第7次比较时, \(A[i]=24,A[j]=20\) ,将较小的元素20放入数组B中, \(j\) ++, \(k\) ++ 。
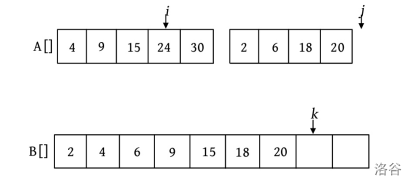
此时, \(j\) >high的后半部分已处理完毕,但前半部分还剩余元素,该怎么办?将剩余元素照搬到数组B就可以了。
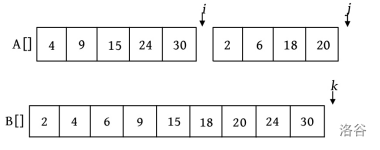
完成合并后,需要把辅助数组B中的元素复制到原来的数组A中。
算法代码:
void Merge(int A[], int low, int mid, int high) { int *B = new int[high - low + 1];//申请一个辅助数组 int i = low, j = mid + 1, k = 0; while (i <= mid && j <= high) {//按从小到大存放到辅助数组B中 if (A[i] <= A[j]) B[k++] = A[i++]; else B[k++] = A[j++]; } while (i <= mid) B[k++] = A[i++];//将数组中剩下的元素放置到数组B中 while (j <= high) B[k++] = A[j++]; for (i = low, k = 0; i <= high; i ++ ) A[i] = B[k++]; delete[] B; }-
合并排序
将序列分成两个子序列,然后对子序列进行递归排序,再把两个已排好序的子序列合并成一个有序的序列。
void MergeSort(int A[], int low, int high) { if (low < high) { int mid = (low + high) / 2;//取中点 MergeSort(A, low, mid);//对A[low : mid]中的元素合并排序 MergeSort(A, mid + 1, high);//对A[mid + 1 : high]中的元素合并排序 Merge(A, low, mid, high);//合并 } }
-
-
算法分析
时间复杂度:分解仅仅是计算出子序列的中间位置,需要常数时间 \(O(1)\) 。递归求解两个规模为 \(n / 2\) 的子问题,所需时间为 \(2T(n / 2)\) 。合并算法可以在 \(O(n)\) 时间内完成。所以总运行时间如下:
\[T(n)=\begin{cases} O(1) &\text{n=1}\\ 2T(\frac n 2)+O(n) &\text{n>1} \end{cases}\]当 \(n>1\) 时,递推求解: