引入
线段树是算法竞赛中常用的用来维护区间信息的数据结构。
树状数组可以在 $O(\log n)$ 的时间内实现单点修改、区间查询(求和、求最值、求异或等);而线段树还可以在 $O(\log n)$ 时间内实现区间修改操作,例如将 $[L, R]$ 区间范围内的值都加上一个常数,乘以一个常数,或者都置为某个数。
常规线段树
结构
就我的理解而言,常规的线段树能实现的功能其实与树状数组没什么区别,都只能在 $O(\log n)$ 时间内实现单点修改和区间查询。
线段树的构造:给定一个区间 $[L, R]$,取 $mid = L + (R - L) / 2$,将它划分为 $[L, mid]$ 和 $[mid + 1, R]$ 两个区间,如此递归地划分,直到区间长度为 $1$ 为止,这些父区间和划分为左右两边的子区间,在组织结构上很像二叉树的父结点和子结点,这也就是线段树的名字由来。
我们这里以区间求和为例,线段树的每个结点对应着相应的线段上的点的和,以数组 $a = {1,2,3,4,5,6,7,8,9,10}$ 为例,线段树的结构如图所示:
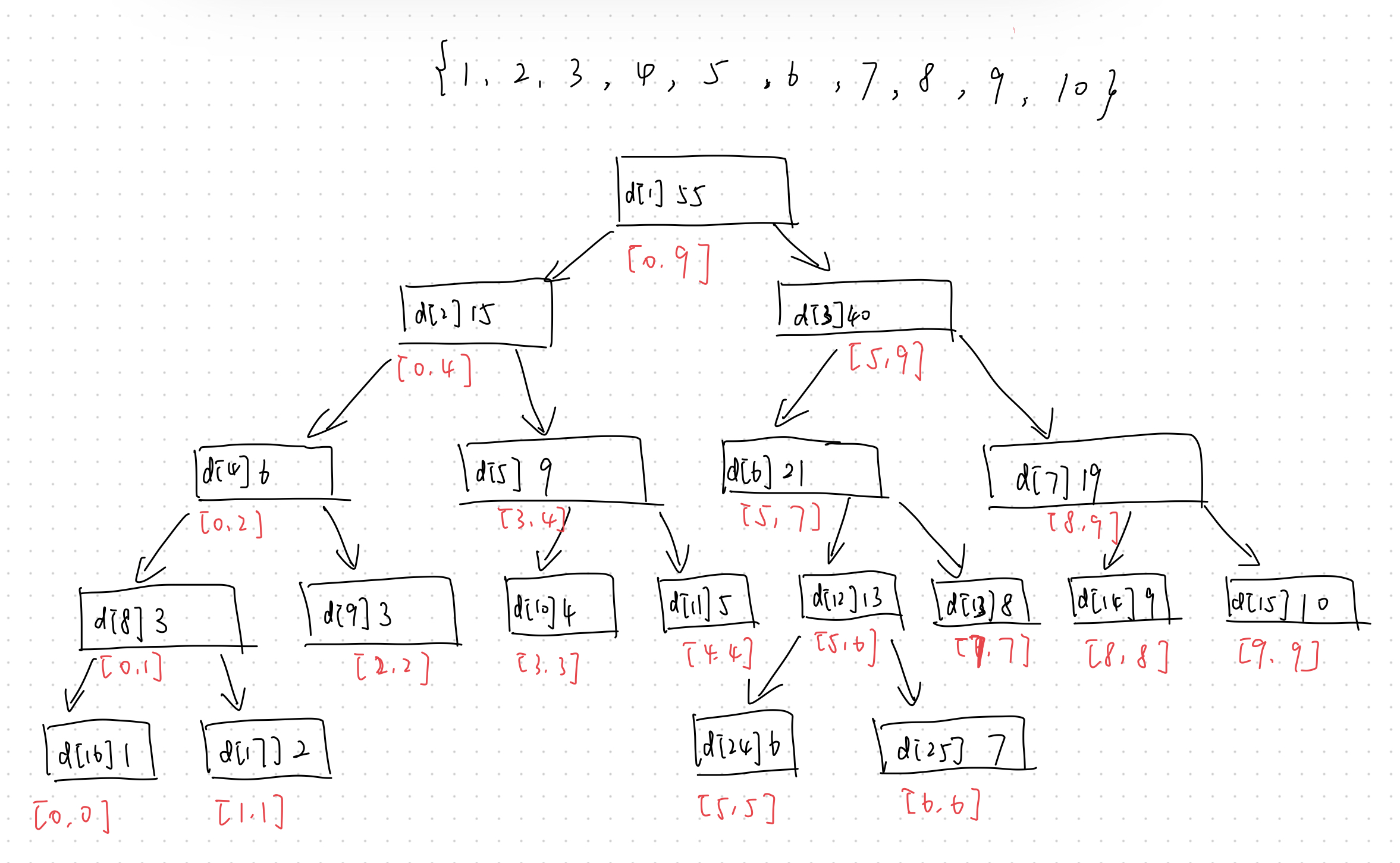
可以看到,线段树存储的基础形式是数组,与二叉堆的存储方式一致,假设当前父结点的编号为 $p$,那么左儿子的编号为 $2 * p$,右儿子的编号为 $2 * p + 1$,结点的值为对应区间的和。
构建线段树的方式其实与“求以该节点为根节点的子树的和”类似,递归处理是很容易的。
代码实现:
void Build(int idx, int l, int r, vector<int> &nums) {
if (l == r) {
seg[idx] = nums[l];
return;
}
int mid = l + (r - l) / 2;
Build(2 * idx, l, mid, nums); // 递归构建左子树
Build(2 * idx, mid + 1, r, nums); // 递归构建右子树
seg[idx] = seg[2 * idx] + seg[2 * idx + 1]; // 更新 seg[idx]
}
区间查询
线段树的区间查询,其实只要掌握了递归,就很好理解了。
我们也是对线段树一层一层地往下查询,先比较待查询区间是否能完全覆盖当前线段树区间,如果能完全覆盖,则返回当前区间的值;否则继续比较待查询区间 $[L, R]$ 与当前区间的 $mid$ 的大小,如果 $L \leq mid$,则递归查询左子区间 $[l, mid]$,如果 $R > mid$,则递归查询右子区间 $[mid + 1, R]$。
例如我们要查询 $[1, 7]$,先考察线段树结点 $1$,它的 $mid$ 为 $4$,于是左子区间和右子区间都要递归查询:
- 左子区间 $[0, 4]$ 的 $mid$ 为 $2$,继续递归查询左子区间和右子区间;
- 区间 $[0,2]$ 还要继续往下查询,右子区间 $[3,4]$ 被待查询区间覆盖,直接返回;
- 右子区间 $[5, 9]$ 的 $mid$ 为 $7$,继续递归查询左子区间 $[5, 7]$,发现区间 $[5, 7]$ 被待查询区间 $[1, 7]$ 完全覆盖,于是直接返回;
最后返回的区间为 $[1,1], [2,2],[3,4],[5,7]$,和为 $35$。
代码实现:
int Query (int idx, int l, int r, int L, int R) { // [L, R] 表示待查询区间
if (L <= l && R >= r) { // 当前区间被待查询区间完全覆盖
return seg[idx];
}
int sum = 0;
if (L <= mid) {
sum += Query(2 * idx, l, mid, L, R); // 递归查询左子区间,左子区间索引为 2 * idx
}
if (R > mid) {
sum += Query(2 * idx, mid + 1, r, L, R); // 递归查询右子区间
}
return sum;
}
对线段树的单点修改,也是一层层遍历线段树,修改对应区间的和即可,如果只有单点修改而不存在区间修改,那么一般用树状数组就能解决,因此这里就不给出单点修改的实现了。
带 Lazy 标记的线段树
前面提到,常规的线段树,个人认为相比树状数组其实没什么优势,时间复杂度的常数还大,占用空间也大,假设待处理的数组 $nums$ 的 $size()$ 为 $n$,那么我们一般要开一个长度为 $4n$ 数组来存储线段树。
即 int seg[4 * n] = {0};。
那为什么说线段树支持 $O(\log n)$ 时间复杂度的区间修改呢,这就需要 Lazy 标记出马了。
int todo[4 * n] = {0};,这里的 $todo[idx]$ 就是所说的 Lazy 标记了。
Lazy 标记,简单来说,就是通过延迟对子节点信息的修改,从而减少可能的不必要的操作次数。每次执行修改时,我们通过打标记的方法表明该节点 $idx$ 对应的区间在某一次操作中被更改,同时更新 $seg[idx]$,但是,我们选择先不更新子节点的信息,而是等到 $idx$ 的区间被“破坏”时,再更新子区间,这里说的区间被破坏,就是指我们要更新或者查询 $idx$ 区间对应的子区间的情况。
例如,第一次更新,我们需要对区间 $[0, 4]$ 都 $+1$,经过遍历,我们知道区间 $[0, 4]$ 对应的 $idx$ 是 $1$,因此我们更新 seg[1] += 5;,同时将 todo[1] += 1;,这就是给 $idx = 1$ 打上了 Lazy 标记。
下一次更新或者查询,我们要对区间 $[3, 4]$ 都 $+2$,显然它是区间 $[0, 4]$ 的子区间,因此发生了对区间 $idx = 1$ 的“破坏”,于是我们需要把 Lazy 标记往区间 $[0, 4]$ 的左子区间和右子区间传递,因此我们更新 seg[2] += 3, seg[3] += 2;,同时将 todo[2] += todo[1], todo[2] += todo[1], todo[1] = 0;。
从递归的角度上来说,我们还是处于 $idx = 1$ 的这一层,然后继续递归右子结点,到了 $idx = 3$,更新 seg[3] += 2 * 2;,同时将 todo[3] += 2;。
带 Lazy 标记的更新操作具体实现如下:
int seg[4 * n] = {0}, todo[4 * n] = {0};
void Update(int idx, int l, int r, int L, int R, int add) {
if (L <= l && R >= r) {
todo[idx] += add; // 更新 Lazy 标记
seg[idx] += add * (r - l + 1); // 更新线段树
return;
}
int mid = l + (r - l) / 2;
if (todo[idx] != 0) {
// 说明当前区间存在 Lazy 标记。
// 我们要查询的区间没有完全覆盖当前区间,必然还要往下递归
// “破坏”了当前区间,因此将 Lazy 标记传递到左子区间和右子区间
todo[2 * idx] += todo[idx];
seg[2 * idx] += todo[idx] * (mid - l + 1);
todo[2 * idx + 1] += todo[idx];
seg[2 * idx + 1] += todo[idx] * (r - mid);
todo[idx] = 0;
}
if (L <= mid) {
Update(2 * idx, l, mid, L, R, add); // 递归更新左子树
}
if (R > mid) {
Update(2 * idx + 1, mid + 1, r, L, R, add); // 递归更新右子树
}
seg[idx] = seg[2 * idx] + seg[2 * idx + 1]; // 更新“更新了左右子树”之后的当前区间和
}
带 Lazy 标记的查询其实与更新类似,当查询区间完全覆盖当前区间时,直接 return seg[idx]; 即可,因为当前区间的值已经是最新的了,只是子区间并没有更新(我们这里也不需要子区间的值);
没有完全覆盖时,就跟更新操作一样,出现了“破坏”当前区间的情况,因此更将 Lazy 标记传递到子区间,再继续递归;
int Query(int idx, int l, int r, int L, int R) {
if (L <= l && R >= r) {
return seg[idx]; // 配合上面的 Update 可知,打上 Lazy 标记时,当前区间的值已经更新,只是没有更新子区间
}
int mid = l + (r - l) / 2;
if (todo[idx] != 0) {
// 说明当前区间存在 Lazy 标记。
// 我们要查询的区间没有完全覆盖当前区间,必然还要往下递归
// “破坏”了当前区间,因此将 Lazy 标记传递到左子区间和右子区间
todo[2 * idx] += todo[idx];
seg[2 * idx] += todo[idx] * (mid - l + 1);
todo[2 * idx + 1] += todo[idx];
seg[2 * idx + 1] += todo[idx] * (r - mid);
todo[idx] = 0;
}
int sum = 0;
if (L <= mid) {
sum += Query(2 * idx, l, mid, L, R);
}
if (R > mid) {
sum += Query(2 * idx + 1, mid + 1, r, L, R);
}
return sum;
}