[BJOI2014]大融合

题目描述

小强要在 \(N\) 个孤立的星球上建立起一套通信系统。这套通信系统就是连接 \(N\) 个点的一个树。

这个树的边是一条一条添加上去的。

在某个时刻，一条边的负载就是它所在的当前能够联通的树上路过它的简单路径的数量。

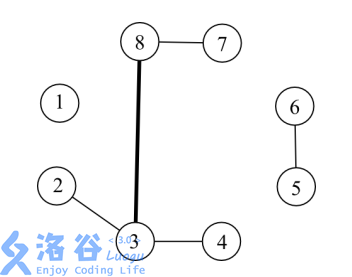
例如，在上图中，现在一共有了 \(5\) 条边。其中，\((3,8)\) 这条边的负载是 \(6\)，因为有六条简单路径 \(2-3-8\),\(2-3-8-7\),\(3-8,3-8-7\),\(4-3-8\),\(4-3-8-7\) 路过了 \((3,8)\)。

现在，你的任务就是随着边的添加，动态的回答小强对于某些边的负载的询问。

输入格式

第一行包含两个整数 \(N, Q\),表示星球的数量和操作的数量。星球从 \(1\) 开始编号。

接下来的 \(Q\) 行，每行是如下两种格式之一：

• A x y 表示在 \(x\) 和 \(y\) 之间连一条边。保证之前 \(x\) 和 \(y\) 是不联通的。
• Q x y表示询问 \((x,y)\) 这条边上的负载。保证 \(x\) 和 \(y\) 之间有一条边。

输出格式

对每个查询操作，输出被查询的边的负载。

样例 #1

样例输入 #1

8 6
A 2 3
A 3 4
A 3 8
A 8 7
A 6 5
Q 3 8

样例输出 #1

6

提示

对于所有数据，\(1≤N,Q≤10^5\)

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#define lid (tree[id].lson)
#define rid (tree[id].rson)

using namespace std;

int fa[5211314];
char ch[5211314];
int n, q, tot;
int cnt, head[5211314], nex[5211314], to[5211314];
int ask1[5211314], ask2[5211314];
int dfn[5211314], max_dfn[5211314], newid;
bool flag[5211314];
int anc[5211314], root[5211314];

struct Segment_Tree {
	int lson, rson;
	int sum;
}tree[5211314];

inline void AddPoi(int v1, int v2) {
	++ cnt;
	nex[cnt] = head[v1];
	head[v1] = cnt;
	to[cnt] = v2;
	return;
}

inline int read() {
	int x = 0, f = 1;
	char ch = getchar();
	while (ch < '0' || ch > '9') {
		if (ch == '-') f = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch - '0');
		ch = getchar();
	}
	return x * f;
}

void DFS(int now, int ancestor) {
	anc[now] = ancestor;
	//记录当前节点所在树的祖先
	max_dfn[now] = dfn[now] = ++ newid;
	//将当前节点子树的dfn处理出来
	for (int i = head[now]; i != 0; i = nex[i]) {
		if (flag[to[i]] == false) {
			flag[to[i]] = true;
			DFS(to[i], ancestor);
			max_dfn[now] = max_dfn[to[i]];
		}
	}
	return;
}

struct MergeSegmentTree {
	inline void PushUp(int id) {
		tree[id].sum = tree[lid].sum + tree[rid].sum;
		return;
	}
	void Update(int &id, int l, int r, int pos) {
		if (id == 0) id = ++ tot;
		if (l == r) {
			tree[id].sum ++;
			return;
		}
		int mid = (l + r) >> 1;
		if (pos <= mid) Update(lid, l, mid, pos);
		else Update(rid, mid + 1, r, pos);
		PushUp(id);
		return;
	}
	int Merge(int a, int b, int l, int r) {
		if (!a || !b) return a + b;
		if (l == r) {
			tree[a].sum += tree[b].sum;
			return a;
		}
		int mid = (l + r) >> 1;
		tree[a].lson = Merge(tree[a].lson, tree[b].lson, l, mid);
		tree[a].rson = Merge(tree[a].rson, tree[b].rson, mid + 1, r);
		PushUp(a);
		return a;
	}
	int Query(int id, int l, int r, int vl, int vr) {
		if (id == 0) return 0;
		if (vl <= l && r <= vr) {
			return tree[id].sum;
		}
		int mid = (l + r) >> 1, ans = 0;
		if (vl <= mid) ans += Query(lid, l, mid, vl, vr);
		if (mid < vr) ans += Query(rid, mid + 1, r, vl, vr);
		return ans; 
	}
}t;

int Find(int x) {
	if (fa[x] == x) return x;
	else return fa[x] = Find(fa[x]);
}

int main() {
	n = read();
	q = read();
	for (int i = 1; i <= q; ++ i) {
		ch[i] = getchar();
		while (ch[i] != 'A' && ch[i] != 'Q') ch[i] = getchar();
		ask1[i] = read();
		ask2[i] = read();
		if (ch[i] == 'A') {
			AddPoi(ask1[i], ask2[i]);
			AddPoi(ask2[i], ask1[i]);
		}
	}
	for (int i = 1; i <= n; ++ i) {
		fa[i] = i;
		if (flag[i] == false) {
			flag[i] = true;
			DFS(i, i);//离线处理每个点的dfn
		}
	}
	for (int i = 1; i <= n; ++ i) {
		t.Update(root[i], 1, n, dfn[i]);
		//注意插入要按dfn的值插入 并且要在跑完dfn后插入 
	}
	for (int i = 1; i <= q; ++ i) {
		if (ch[i] == 'A') {
			int x = Find(ask1[i]);
			int y = Find(ask2[i]);
			//记得找ask1[i]和ask2[i]所在的线段树的根
			fa[y] = x;
			t.Merge(root[x], root[y], 1, n);
			//进行合并
		}
		else {
			int rt = Find(ask1[i]), son;
			int l1 = dfn[anc[ask1[i]]], r1 = max_dfn[anc[ask1[i]]];
			if (dfn[ask1[i]] > dfn[ask2[i]]) son = ask1[i];
			else son = ask2[i];//找dfn大的点(即找为儿子点)
			int ans_anc = t.Query(root[rt], 1, n, l1, r1);
			int ans_son = t.Query(root[rt], 1, n, dfn[son], max_dfn[son]);
			//儿子节点dfn范围内的sum值即为儿子节点所在连通块的大小
			//祖先的dfn范围内的sum减去儿子点dfn范围内的sum即为父亲节点所在连通块的大小
			printf("%d\n", (ans_anc - ans_son) * ans_son);
			//边左边的点的个数乘边右边的点的个数即为边的负载
		}
	}
	return 0;
}