1 引言
B-tree,B即Balanced,是自平衡的多叉搜索树,用于组织和存储大量数据,以及数据库和文件系统等需要高效查找和插入操作的应用中。
为什么是“大量数据”?当主存不足以放入大量数据时,不常用的数据应存储于外存,而访问外存有额外时间开销(如磁盘转动时间、磁头移动时间等),于是我们需要一个数据结构来减少磁盘访问次数。
B树每个节点包含多个关键字(键)和对应的数据指针(节点),关键字按照大小排序,并且每个节点的关键字都对应子节点的范围。
B树的根节点存储在主存中,而其他节点存储在磁盘或其他外部存储设备上。
M阶B树是有以下特性的M叉树:
- 数据项(data items)存储在叶节点(leaves);
- 非叶节点(nonleaf nodes)最多存储指引搜索路线的M-1个关键字Key,并且Key i是该节点子树i+1的最小值;
- 根节点(root)也是非叶节点,它有2至M个子节点;
- 所有非叶节点(root除外)有\(\lceil M/2 \rceil\)至M个子节点;
- 所有叶节点都位于最底层,有\(\lceil L/2 \rceil\)至L个数据项。L是指定值,由存储块和记录大小决定,即L=存储块大小/记录大小。
五阶B树示例如下图所示:
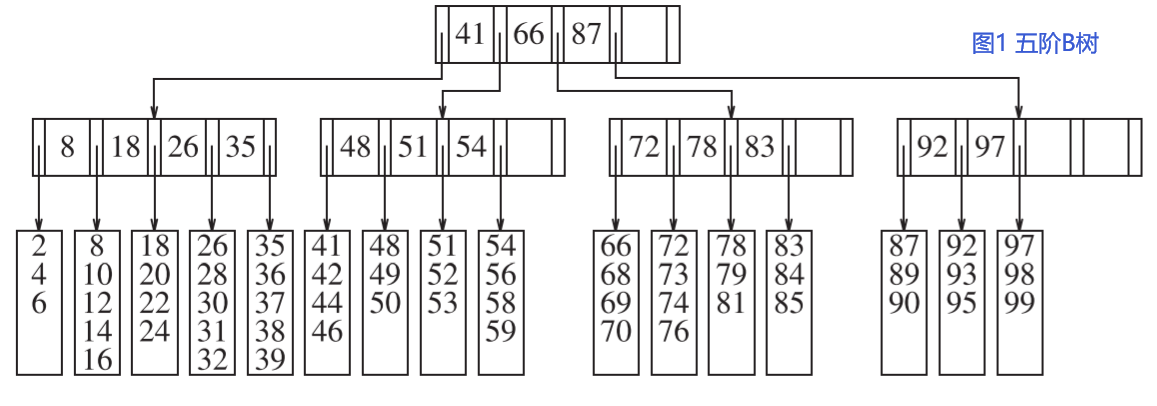
上图中,M=5,L=5,于是,根节点有2到5个子节点,非叶节点最多有4个关键字,除根节点外的非叶结点有3到5个子节点,叶节点有3到5个数据项。每个节点都是一个磁盘块(disk block)。
2 B树的操作
添加
如图2,插入57到图1。
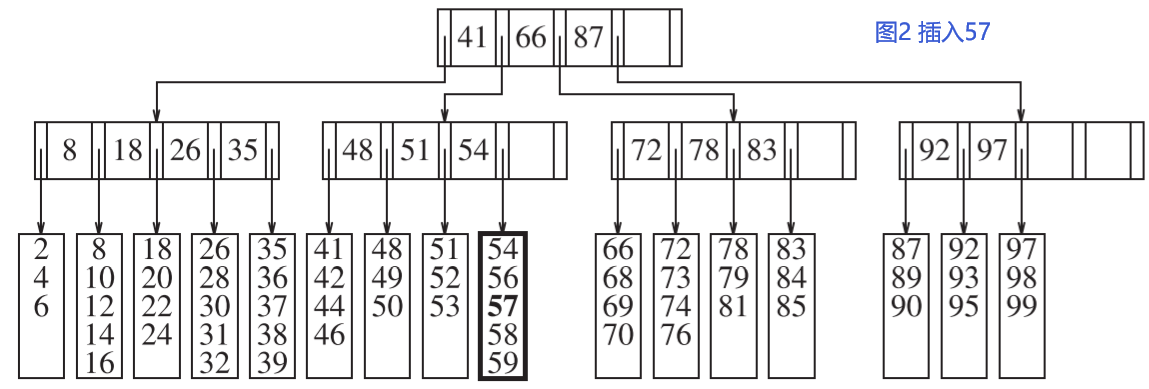
插入操作步骤如下:
- 从根节点开始,按照键值的大小进行搜索,直到找到合适的叶子节点。在这个例子中,我们找到了可以插入57的叶子节点。
- 检查叶子节点是否已满。如果叶子节点未满,则可以直接将57插入到适当的位置。
- 如果叶子节点已满,需要进行节点的分裂操作。首先,将叶子节点中的数据项和新的数据项按照键值的顺序重新排序。然后,将前一半数据项保留在原始叶子节点中,将后一半数据项移动到新创建的叶子节点中。同时,更新父节点中的键值和分支信息,以反映新的叶子节点的存在。
- 如果父节点也已满,可能需要继续进行分裂操作,以保持B树的平衡性。
如图3,插入55到图2,共两步:分裂页节点和更新父节点。所以一共有三次disk write操作。
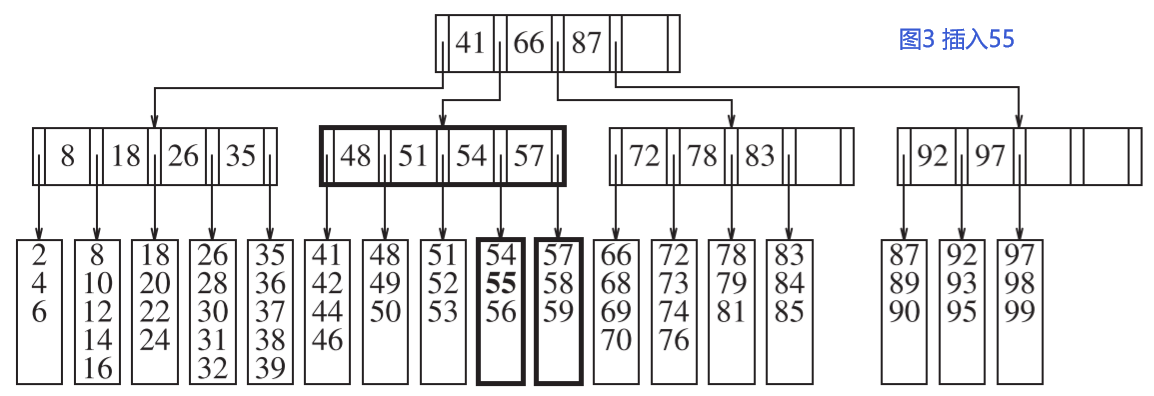
如图4,插入40到图3,由于父节点满项,所以除了分裂子节点,更新父节点,还需要再分裂父节点。一共五次disk write。
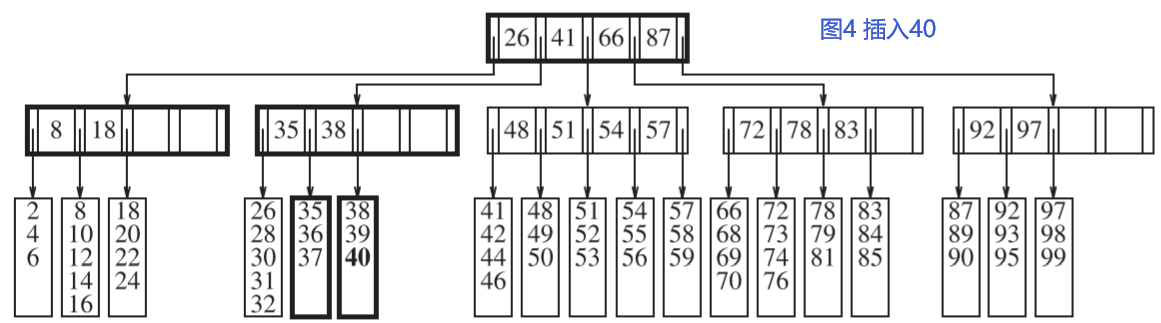
添加操作可能导致的根节点分裂是B树高度增加唯一方式。
删除
flowchart TD A(寻找键值) ==> B{是否存在} B ==是==> C[删除键值] B ==否==> D(结束) C ==> E{该节点是否符合最小占用} E ==是==> D E ==否==> F{邻居节点是否比最小占用多} F ==是==> G[从邻居节点借一个] F ==否==> H[合并邻居节点] G ==> D H ==> I{父节点是否符合最小占用} I ==是==> D I ==否==> J{是否为根节点} J ==否==> F J ==是==> K{根节点是否只有一个子节点} K ==否==> D K ==是==> L[删除根节点,子节点作为新根节点] L ==> D上图删除根节点是B树高度减小的唯一方式。
标签:数据项,存储,叶子,插入,键值,数据结构,节点 From: https://www.cnblogs.com/LiJunLin1231/p/17459888.html