DRTREE - Dynamically-Rooted Tree
本题建议评蓝。
思路:
题目就是要对一颗不定根树求子树权值和。
这题不带修,如果带修难度会增加一点,就跟 遥远的国度 差不多。
首先分析一下在以不同根下子树的变化。
当一颗树以 1 号节点为根时,比如说长这样:
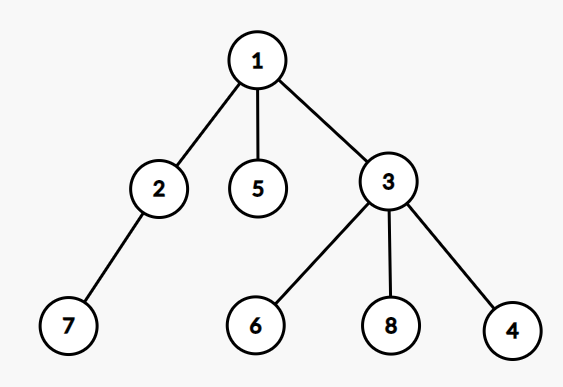
假设每个点的权值为 1,那么这 8 个点的子树权值和(在这里也是子树大小)分别为:8,2,4,1,1,1,1,1。这是可以通过预处理得到的。
而当整个树的根变化后,我们分情况讨论:(假设变化后的根为 \(A\),要求的点为 \(B\))
-
当 \(A=B\) 时,毫无疑问答案是整个树的权值和。
-
当 \(A\) 不在 \(B\) 的子树中时,我们发现,\(B\) 的子树不会发生变化,那么子树权值和也就是在以 1 为根的情况下的权值和。
-
当 \(A\) 在 \(B\) 的子树中时,情况复杂起来了。举个例子,比如说在上图中,将根换成 8 号节点,求 3 号节点:
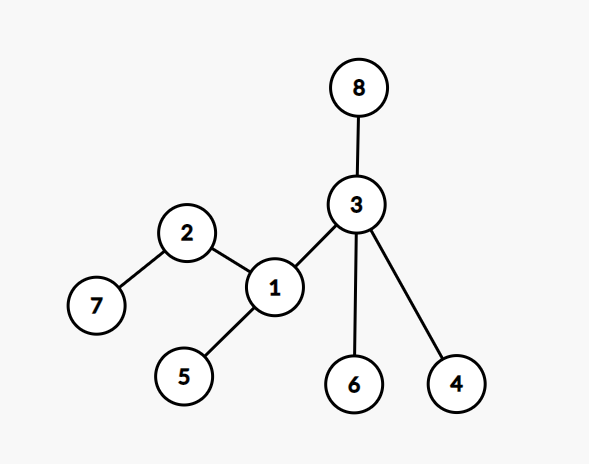
我们可以发现,这时的 3 号节点的子树权值和变成了:树的权值总和减去 3 号点在 8 号点方向的子树的权值和。(这个例子可能不太好,可以自己画几个图模拟一下。)
因此我们可以得出结论:在这种情况下,答案就是树的权值和减去 \(B\) 在 \(A\) 方向上的子树的权值和。
还剩下几个问题:
怎么判断一个点 \(A\) 是不是在另一个点 \(B\) 的子树中?
方法很多,有的简单有的相对麻烦。
比如说求 \(A\),\(B\) 的 \(\text{LCA}\) ,看看是不是 \(B\),时间复杂度为 \(O(\log n)\)。
再比如说用树剖加线段树,将 \(B\) 的“权值”设为 \(1\) ,其他的点设为 \(0\),判断从点
\(A\) 到 \(1\) 的路径上的“权值”最大值是不是 \(1\),时间复杂度为 \(O(\log ^2n)\)。
这里我们使用了最简单也是最快的方法,利用 \(\text{dfs}\) 序进行判断。
(我们用 \(\text{dfn}\) 表示 \(\text{dfs}\) 序,\(\text{size}\) 表示子树大小。)
因为当且仅当 \(\text{dfn}[B]\le \text{dfn}[A] \le \text{dfn}[B]+\text{size}[B]-1\) 时,点 \(A\) 会在 \(B\) 的子树中,故可以通过这个式子进行判断,时间复杂度为 \(O(1)\)。
怎么求一个点 \(A\) 在 另一个点 \(B\) 的方向上的子树权值和?(点 \(B\) 在 \(A\) 的子树内)
因为我们预处理了子树权值和,所以我们只需要求出点 \(A\) 在点 \(B\) 方向上的儿子就可以了。
我们可以用树剖解决这个问题(当然,倍增也可以,但更慢。):
我们按链一段段跳,如果跳的途中发现某点所在的链顶的父亲是另一个点,那么返回链顶。如果一直跳到了最后,因为此时两点在同一条链上,所以这时返回深度较小的点的重儿子就行了。
int lcason(int x,int y){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) Swap(x,y);
if(fa[top[x]]==y) return top[x];
x=fa[top[x]];
}
if(dep[x]>dep[y]) Swap(x,y);
return son[x];
}
注意事项:
加边方式比较奇怪,注意一下。
点权较大,记得开 long long 。
代码:
#include <bits/stdc++.h>
using namespace std;
const int N=200100;
typedef long long ll;
int to[N],nxt[N],head[N],w[N];//链星
int dfn[N],siz[N],top[N],dep[N],son[N],fa[N],rnk[N];//树剖
int idx,n,q,in1,cnt,rt=1;
ll W[N],sum,ans;//W表示子树权值和
char op[2];
void add(int u,int v){idx++;to[idx]=v;nxt[idx]=head[u];head[u]=idx;}
void Swap(int &x,int &y){int t=x;x=y;y=t;}
void dfs_1(int s,int gr){
siz[s]=1;son[s]=-1;fa[s]=gr;
dep[s]=dep[gr]+1;
W[s]=w[s];sum+=w[s];//预处理子树权值和
for(int i=head[s];i;i=nxt[i]){
int v=to[i];
if(v==gr) continue;
dfs_1(v,s);
siz[s]+=siz[v];W[s]+=W[v];
if(son[s]==-1||siz[v]>siz[son[s]]) son[s]=v;
}
}
void dfs_2(int s,int tp){
top[s]=tp;dfn[s]=++cnt;rnk[cnt]=s;
if(son[s]==-1) return ;
dfs_2(son[s],tp);
for(int i=head[s];i;i=nxt[i]){
int v=to[i];
if(v==fa[s]||v==son[s]) continue;
dfs_2(v,v);
}
}
int lcason(int x,int y){//求某点在另一个点方向上的儿子
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) Swap(x,y);
if(fa[top[x]]==y) return top[x];
x=fa[top[x]];
}
if(dep[x]>dep[y]) Swap(x,y);
return son[x];
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&w[i]);
for(int i=1;i<n;i++){
scanf("%d",&in1);
add(in1,i+1);add(i+1,in1);//加边
}
dfs_1(1,0);dfs_2(1,1);//先以1为根跑树剖
scanf("%d",&q);
while(q--){
scanf("%s%d",op+1,&in1);
if(op[1]=='S'){
if(rt==in1) ans=sum;
else if(dfn[in1]<=dfn[rt]&&dfn[rt]<=dfn[in1]+siz[in1]-1) ans=sum-W[lcason(in1,rt)];
else ans=W[in1];//我们讨论过的三种情况
cout<<ans<<'\n';
}
if(op[1]=='R') rt=in1;
}
return 0;
}
其他:
类似的题目:
P3979 遥远的国度,
Jamie and Tree(这两个都带修)。