你是什么仙人?
引入
仙人掌是一种特殊的无向图,它的任意一条边至多只出现在一条简单回路(每个点只出现一次的回路是简单回路,特殊地,自环不算简单回路)。
这里借用一下 [SHOI2006] 仙人掌 中的图片。
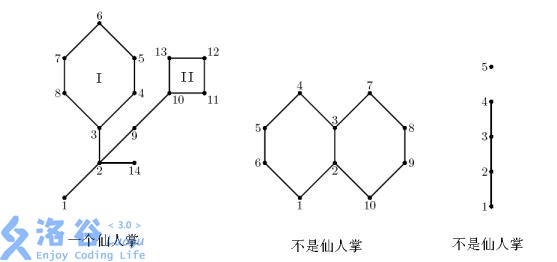
仙人掌的特殊性质使得某些问题(如两点最短路)有更为高效的算法,其中圆方树是求解仙人掌的有力工具,但圆方树的性质又不止于此。
例题
【模板】静态仙人掌 / Freda 的传呼机
洛谷传送门
没有双倍经验,别想了。
给定一个 \(n\) 点 \(m\) 边的仙人掌,进行 \(q\) 次询问,每次询问仙人掌上两点间的最短路径。\(n,q\leq 10^4,m\leq2\times 10^4\),时间限制为 \(300\text{ms}\)。
解析:先思考一下,如果给定的是一棵树而非仙人掌如何求解。对于一棵树而言,任意两点间的路径是唯一确定的,因此问题转化为快速求树上两点权值和。
用什么算法呢?当然是 LCT 树上差分了。类比序列上的差分操作,我们记录下每个点到根节点的权值和。那么对于任意两点,只要找到它们的最近公共祖先,答案就是两点到根节点的权值和相加减去祖先到根节点的权值的两倍(因为两个节点都算了一次)。
现在考虑仙人掌。对于每一个环,我们都可以通过 tarjan 算法缩点。设缩点后得到的点为方点,原图的点(没有形成环)为圆点,就可以得到一棵圆方树。需要注意的是,圆方树是一棵有向树,从父节点指向子节点。
下面这张图来自 WC2018 的讲课论文,展示了圆方树的构建过程。

讨论仙人掌转圆方树的具体过程:
- 任取一点作为根。
没根玩锤子呢 - 对于仙人掌上的每一个环,找到这个环与根距离最近的点(即环的“头部”),然后将环的头部向认为建立的方点连边,方点与剩下的点连边。
- 为保证环与树的等价,我们定义头部点与方点边权为 \(0\),方点与剩余点的边权为头部与剩余点的最短距离。
但需要注意的是,圆方树建立后仍然不能直接树上差分求最短路。当两点的最近公共祖先为方点(即原图的环),则需要对其进行分类讨论,即找到对应环上哪两个点并且去较短的一侧。
这么说起来有点抽象,直接看代码吧 >_<
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int maxn = 5e4 + 10;
int n, m, q, sign, a, b; //sign 标记方点编号,a 和 b 在求 lca 时要用
int head1[maxn], head2[maxn], nxt[maxn], to[maxn], val[maxn], cnt; // 两个 head 分别存原图和圆方树
/*只要建两个表头就可以让两张图互不干涉,不需要写别的*/
int dfn[maxn], low[maxn], idx;
int sum[maxn], len[maxn]; //记录点到根的权值和以及环内点到头部点的距离
int anc[maxn][20], dep[maxn], dis[maxn];
int fa[maxn], fw[maxn], fe[maxn]; //圆方树内的父节点,与父节点连边权值,与父节点连边的编号
void add(int head[], int u, int v, int w) {
nxt[cnt] = head[u], to[cnt] = v, val[cnt] = w, head[u] = cnt++;
}
void buildCircle(int u, int v, int w) {
int s = w;
for (int k = v; k != u; k = fa[k]) {
sum[k] = s;
s += fw[k];
}
sum[u] = len[u] = s;
add(head2, u, ++sign, 0); //方点和头部点连边
for (int k = v; k != u; k = fa[k]) {
len[k] = s;
add(head2, sign, k, min(sum[k], s - sum[k])); //在环两侧中取较小距离连边
}
}
void tarjan(int u, int f) {
dfn[u] = low[u] = ++idx;
for (int i = head1[u]; ~i; i = nxt[i]) {
int v = to[i], w = val[i];
if (!dfn[v]) {
fa[v] = u, fw[v] = w, fe[v] = i;
tarjan(v, i);
low[u] = min(low[u], low[v]);
if (dfn[u] < low[v]) add(head2, u, v, w);
} else if (i != (f ^ 1)) low[u] = min(low[u], dfn[v]);
}
for (int i = head1[u]; ~i; i = nxt[i]) {
int v = to[i], w = val[i];
if (dfn[u] < dfn[v] && fe[v] != i) //fe 防止出现重边时对环的判断出错
buildCircle(u, v, w);
}
}
void initLca(int u, int f) { //对圆方树预处理倍增
dep[u] = dep[f] + 1;
anc[u][0] = f;
for (int i = 1; i <= 15; i++)
anc[u][i] = anc[anc[u][i - 1]][i - 1];
for (int i = head2[u]; ~i; i = nxt[i]) {
int v = to[i], w = val[i];
dis[v] = dis[u] + w;
initLca(v, u);
}
}
int lca(int u, int v) {
if (dep[u] < dep[v]) swap(u, v);
for (int i = 15; i >= 0; i--)
if (dep[anc[u][i]] >= dep[v])
u = anc[u][i];
if (u == v) return u;
for (int i = 15; i >= 0; i--)
if (anc[u][i] != anc[v][i])
u = anc[u][i], v = anc[v][i];
a = u, b = v; //记录最近公共祖先的两个子节点
return anc[u][0];
}
int main(void) {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m >> q;
sign = n;
memset(head1, -1, sizeof(head1));
memset(head2, -1, sizeof(head2));
for (int i = 1; i <= m; i++) {
int u, v, w;
cin >> u >> v >> w;
add(head1, u, v, w);
add(head1, v, u, w);
}
tarjan(1, -1);
initLca(1, 0);
while (q--) {
int u, v, Lca;
cin >> u >> v;
Lca = lca(u, v);
if (Lca <= n) cout << dis[u] + dis[v] - dis[Lca] * 2 << '\n';
/*最近公共祖先为圆点,直接求解*/
else {
int da = dis[u] - dis[a], db = dis[v] - dis[b];
int dm = min(abs(sum[a] - sum[b]), len[a] - abs(sum[a] - sum[b]));
/*最近公共祖先为方点,取环内较小值作为贡献*/
cout << da + dm + db << '\n';
}
}
return 0;
}