简介

模拟退火 （\(\text{Simulate Anneal}\)） 和爬山法是随机化算法，二者的原理都在于通过随机生成答案并检查，把答案逐步缩小在一个可行的区间，尽可能地靠近正确答案。
在考场中，如果某道题目的正解比较难想（例如性质复杂的贪心）或者对应的函数取值可能数极大且难以二分/三分求解时，模拟退火和爬山法可以一定程度上得到正确答案并获得可观的分数。
顺带一提，现在的人工智能其实也是基于随机化算法的，例如遗传算法就是一种典型的随机化算法。
高情商：利用人工智能算法获取近似解
低情商：随机骗分

原理

下面主要讲模拟退火，爬山法只提一点。

顾名思义，模拟退火就是模拟物理学上的退火过程。类比分子在高温时能量更高、碰撞次数更大的原理（参见《化学反应原理》P28），我们定义几个量：

• 温度 \(T\)：相当于答案区间，控制每次随机区域。一开始的 \(T\) 为较大值，接下来逐步减小。
  \(T\) 有初始态 \(T_0\)、终止态 \(T_k\) 和降温系数 \(d\) 三个关联量。一般来说 \(T\) 取值较大，\(T_k\) 接近 \(0\)，\(d\) 略小于 \(1\)。这样每次让 \(T\) 乘以 \(d\) 就可以实现“降温”。
• 能量差 \(\Delta E\)，表示新得到答案和原本答案的差值。如果 \(\Delta E<0\)，说明答案更优，应取该答案；反之，以一定概率取这个答案，从而减小落入局部最优解的可能性。
  通常取概率值为 \(e^{\frac{-\Delta E}{T}}\)，这样可以保证能量差越高取答案的可能越大。

下面这个图反映了落入局部最优解的坏处（来自 OI-Wiki）。

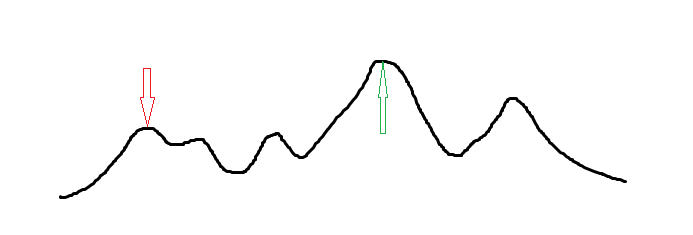
例题讲解

[POJ2420]A Star not a Tree?

洛谷传送门
给定平面直角坐标系上的 \(n\) 个点，找到一个点使得到这些点的欧几里得距离最小（即费马点），输出距离之和（保留整数）。

解析：这道题的答案是一个凸函数，可以用三分法求解，这里演示一下模拟退火。
模拟退火写起来其实非常无脑xwx

#include <iostream>
#include <algorithm>
#include <cmath>
#include <random>
#include <iomanip>

using namespace std;

const int maxn = 150;
const double maxTime = 0.95;

random_device rd;
mt19937 Rand(rd());
uniform_real_distribution<double> Dis(0, 1); //随机三件套

struct Point {
    double x, y;
} q[maxn];

int n;
double ans;

inline double rand(double l, double r) { //得到 [l, r) 的数字
    return (double) Dis(Rand) * (r - l) + l;
}

inline double dis(Point a, Point b) { //求欧几里德距离
    double dx = a.x - b.x, dy = a.y - b.y;
    return sqrt(dx * dx + dy * dy);
}

double calcDistance(Point p) { //计算距离和，顺便更新答案
    double res = 0;
    for (int i = 1; i <= n; i++) res += dis(p, q[i]);
    ans = min(ans, res);
    return res;
}

void simulateAnneal() {
    Point cur = {rand(0, 1e4), rand(0, 1e4)};
    for (double T = 1e4; T > 1e-4; T *= 0.99) {
        Point p = {rand(cur.x - T, cur.x + T), rand(cur.y - T, cur.y + T)}; //在范围内随机取一个新点
        double delta = calcDistance(p) - calcDistance(cur);
        if (exp(-delta / T) > rand(0, 1)) cur = p; //概率取解
    }
}

int main(void) {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int T;
    cin >> T;
    for (int j = 1; j <= T; j++) {
        ans = 1e8;
        cin >> n;
        for (int i = 1; i <= n; i++) cin >> q[i].x >> q[i].y;
        for (int i = 1; i <= 100; i++) simulateAnneal();
        /*如不是多组数据则可以利用“卡时”技巧，下一题会详细讲解*/
        cout << fixed << setprecision(0) << ans << '\n';
        if (j != T) cout << '\n';
    }
    return 0;
}