内容
- 几种BA的形式
- 同时优化相机和三维点
- 优化相机
- 只优化三维点
- 单目相机
- 增量运动恢复结构(Incremental SFM)
- 运动恢复结构的几个问题
几种BA的形式
数学模型
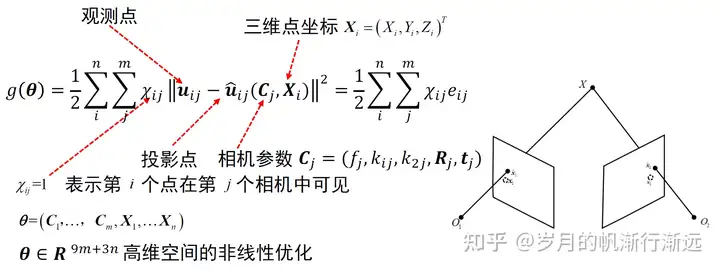
n个三维点和m个相机,一些三维点在相机上的投影点。i表示三维点的索引,j表示相机的索引。 u 表示观测点, u^ 表示理想点
根据当前相机参数和三维点的坐标计算投影点的位置,然后计算观察点和投影点之间的误差,之后通过优化的方法使这个误差最小,从而得到一个比较好的相机参数和三维点的坐标。
该模型是一个非线性的最小二乘。通常采用LM算法~LM算法是一种基于信頼域的算法,通过调整信頼域半径的大小,在最速下降法(使用一阶梯度)和牛顿法(使用二阶梯度,考虑全局)之间切换,更加鲁棒。LM算法的核心是构造增量正规方程,通过方程可以求出增量,然后根据增量对当前的方程进行更新。
如果当前误差比较大,减小信頼域,使方法趋近于牛顿法。如果当前误差比较小,增大信頼域,使方法趋近于最速下降法。

增量正规方程
将 J(θ) 进行排序,P1~P3对应三个相机,X1~X4对应四个三维点。x11是第1个点在第1个相机中的投影。如果4个点在三个相机里都有投影,那么可以得到12个观察点。每个点有x和y坐标,24行;列数为总参数的个数(3个相机x9+4个三维点x3=39)。
JT(θ)J(θ) 是很明显的分块矩阵(方阵)。方阵的行数和列数就是参数的个数。
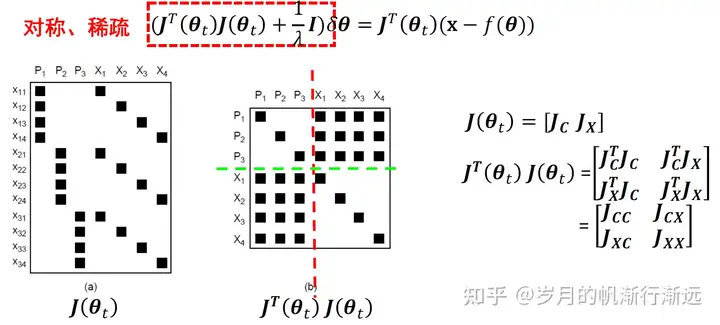
同时优化相机参数和三维点
将信頼域加入其中,只对包含对角线的分块矩阵有影响。

解方程:

得到两个方程,解第一个方程可以得到相机参数的增量 δc ,将δc代入第二个方程可以得到三维点的增量δX。
求解这个方程可以使用共轭梯度法,因为这个方程是比较大的稀疏矩阵。
- 固定三维点坐标,优化相机参数(特殊场景1)
对于三维点的梯度均为0,δX=0。只计算δc。更新相机参数
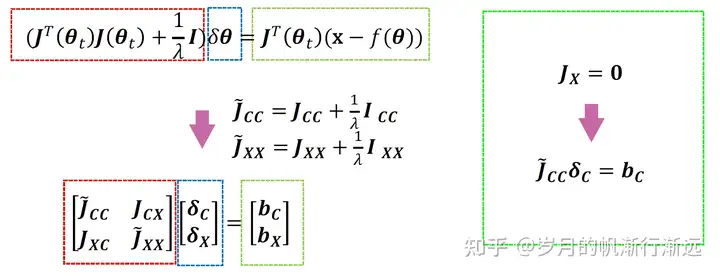
- 固定相机参数(特殊场景2)
只计算三维点的坐标增量δX。在对三维点进行更新。

单目相机——内参数共享(特殊场景3)
使用同一个相机在不同角度拍摄同一物体。这种场景下,相机的内参一致。
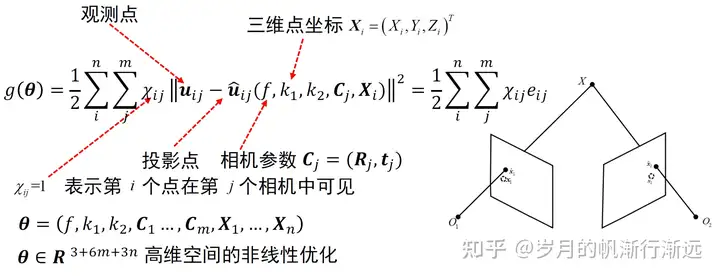
在该模型中,所有的内参(f, k1, k2)一致,将内参从Cj中独立出来。因此这里的 Cj 只表示相机的外参(R, t)。
由于所有相机的内参数固定,所以总的参数个数为(3+6m+3n)。
对之前的Jacobian矩阵进行改变,加入对f, k1, k2的偏导数。

之前使用的 J(θ) 是一个稀疏矩阵。但是由于加入了对于内参数(f, k1, k2)的偏导数,内参数与每个观察点都有关联,因此其对每个观察点都有值。J(θ)的形式发生改变。
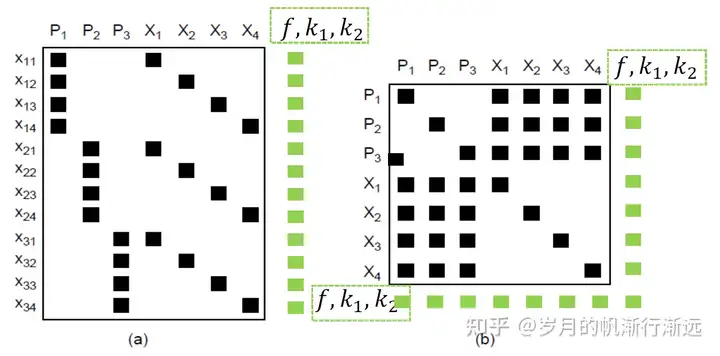
使用的求解方法与之前的求解方法类似。
运动恢复结构(SFM)
通过相机运动同时恢复相机参数(内外参数)和场景结构(三维点坐标)。

这里介绍的场景针对无序图像。有序图像的匹配复杂度会减少很多。无序图像经过SFM得到稀疏点云。之后还可以对其进行稠密的点云重建,对图像进行径向畸变的校正。
主要流程
- 输入图像
- 特征提取与匹配
- 图像连接图构建
- 捆绑调整优化相机姿态和场景结构
- 得到稀疏点云
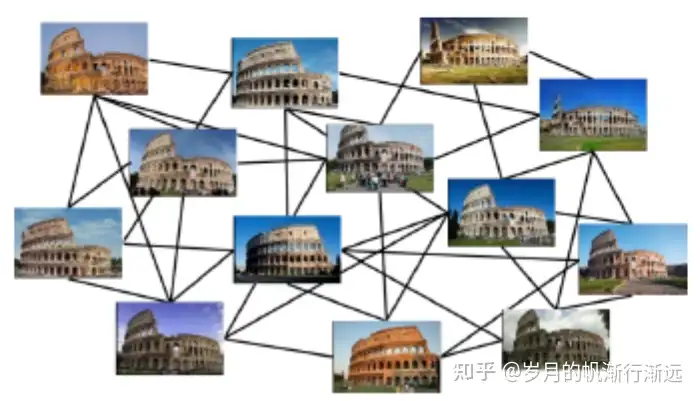
将两两对应关系对齐到同一的坐标系。
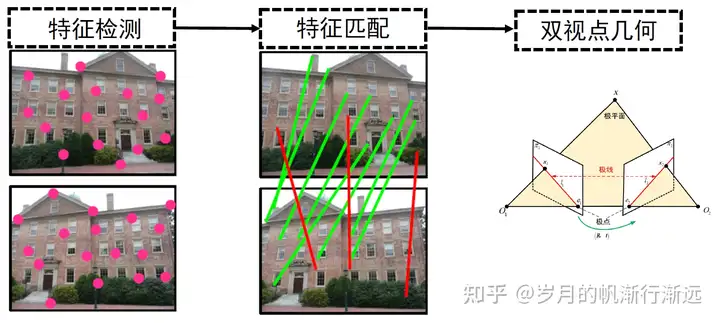
通过特征检测得到特征点,对不同视角的特征点进行匹配。通过对极几何,筛选出外点,保留内点,通过内点拟合出模型,得到相机相对的姿态。
对极几何模型选择:
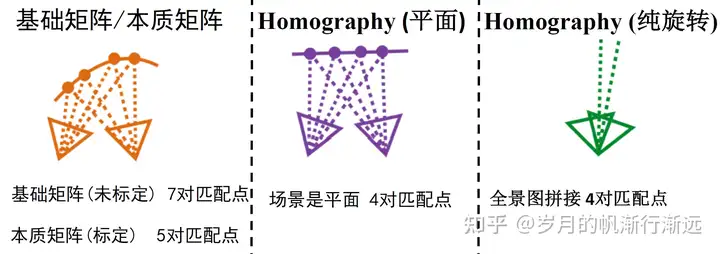
单应矩阵需要场景是平面,场景的深度很深,例如航拍。
图像连接图
连接图的顶点:每张图像
连接图的边界:两幅图像之间存在共同的可见区域(足够多的匹配内点)
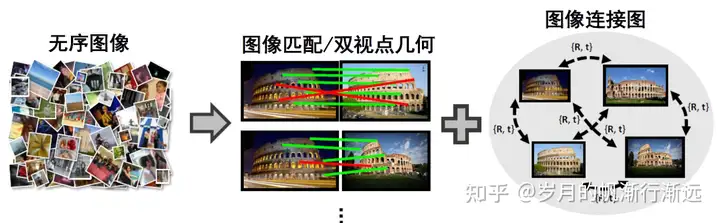
每张图像看多一个节点,对所有图像进行两两匹配,如果两张图像存在足够多的匹配点,那么将两个图像连接起来,其连接线作为一条边界。最终可以得到一个很大的无向图。无向图的顶点是每张图像,边界是两张图像间的匹配关系。该无向图称为图像连接图。
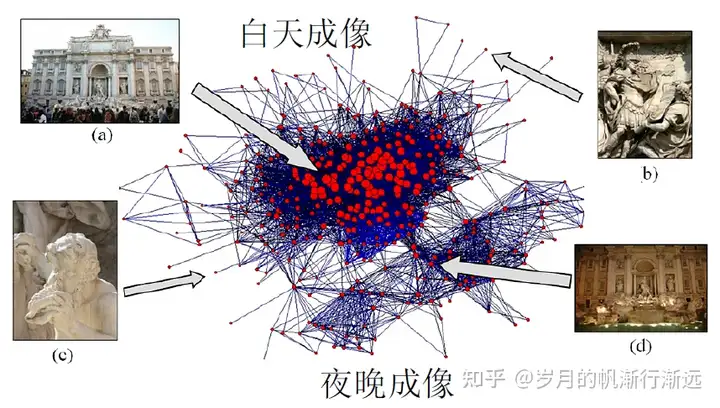
- 顶点的大小与连接个数有关:一个顶点的邻域越多,顶点越大;
- 比较好的视角(相似的、正面光照条件好)集中在中央,偏一些的图像位于集中在边界;
- 白天成像和夜晚成像出现分块的情况。
Tracks
- 多个视角对应的匹配点连接起来
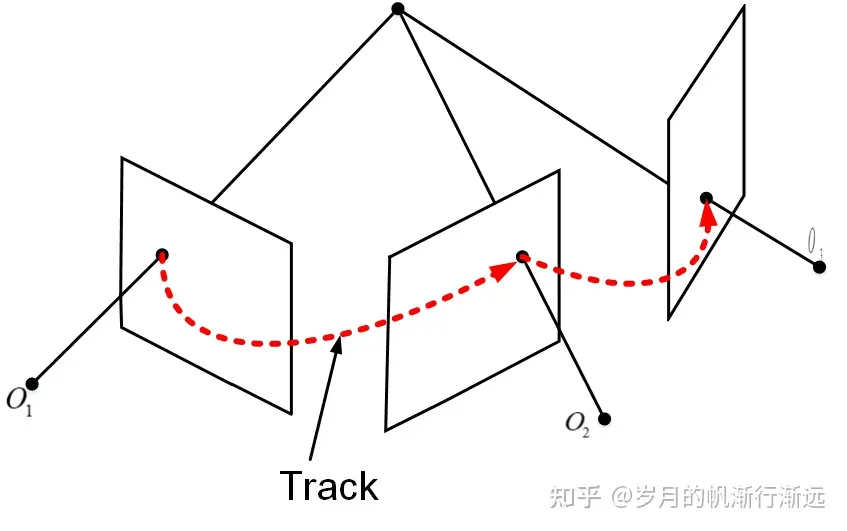

- 一个三维点(匹配点)对应着一个Track
计算Tracks(三维点+匹配关系)
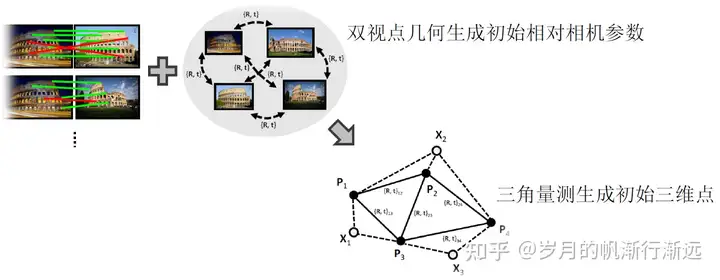
已知图像中各特征点的位置和当前的相机姿态。如果我们知道两个以上特征点的位置,就可以计算三维点的坐标。
Track也可以用来计算相机姿态。
捆绑调整(BA)
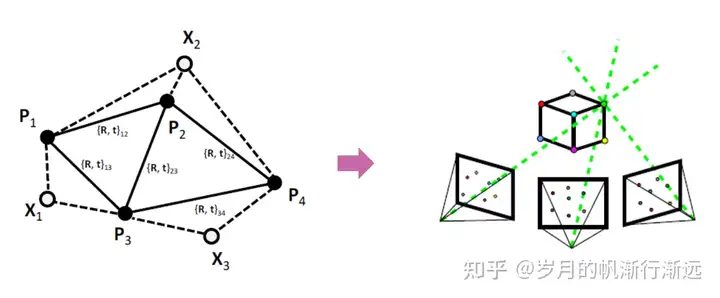
相对的相机参数生成全局一致的相机参数和场景结构。
算法流程
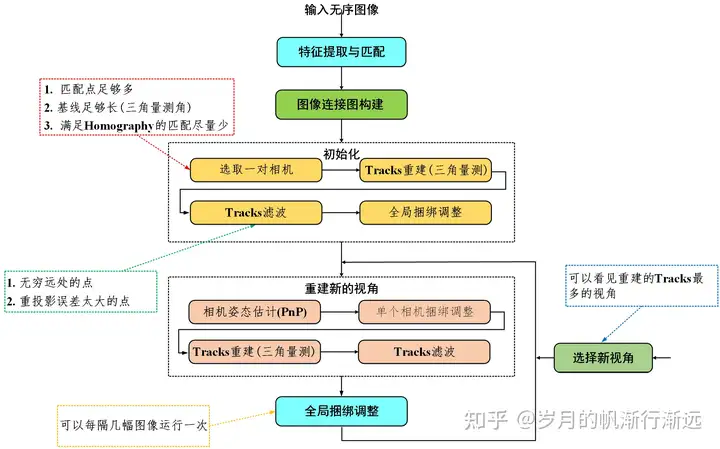
图像连接图,去除末梢的图像,使用视角好的图像进行重建。
要先选择一个视角(一对相机)进行重建。
在这个视角之上,要不断添加新的视角。如何选择新视角是有标准的。
选择新视角后,要对当前的视角进行重建,得到相机参数,对单视角进行优化。这一步只对当前相机进行优化。优化后,track上多了匹配点,再进行滤波。
重建后,进行全局的捆绑调整。为了效率,几张图像调整一次。
增量的运动恢复结构
初始相机对的选取
选择一对图像
- 匹配点足够多(>=50)
- 基线足够长,三角量测的角足够大(>=5deg),$\alpha$为三角量测角
匹配对很多,如何对所有角进行衡量?使用所有夹角的平均值或找中值 - 满足homography尽量少(<60%)
- 成功三角化的匹配对>50%
保证匹配对足够可靠,匹配足够好。
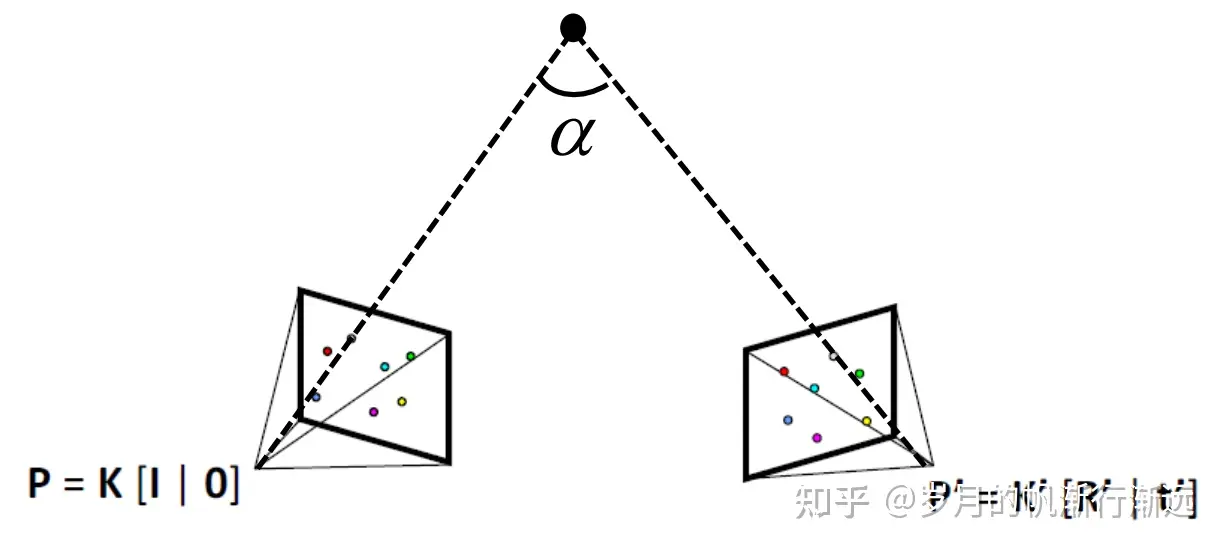
RANSAC三角量测
目前一直相机的两个姿态。
- 使用三角量测,将tracks重建出三维点;
- 由于存在匹配外点,重建出错误的tracks,用RANSAC的方法排除外点
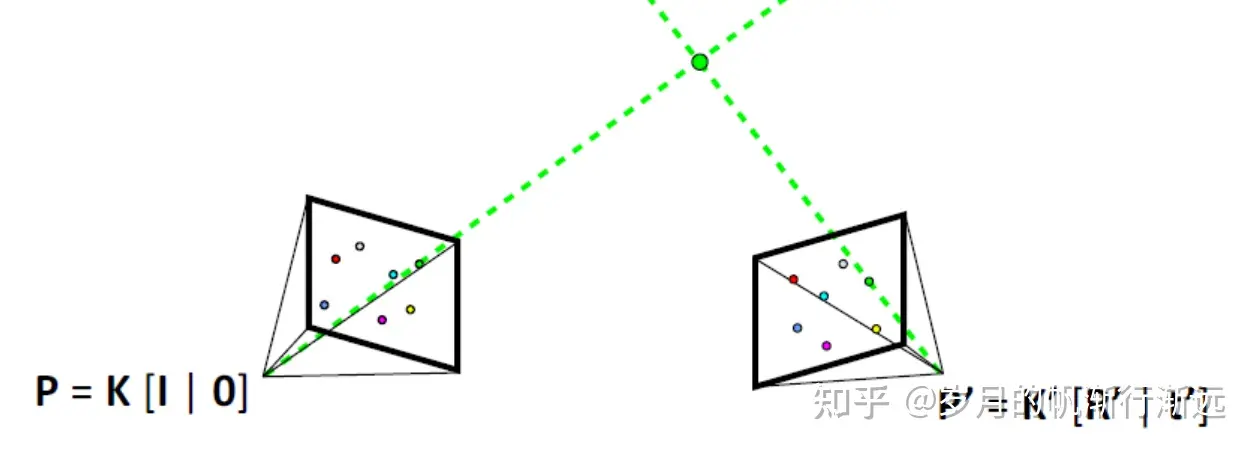
Tracks滤波
- 三维空间中太远的点:将三维点投影到像平面上;
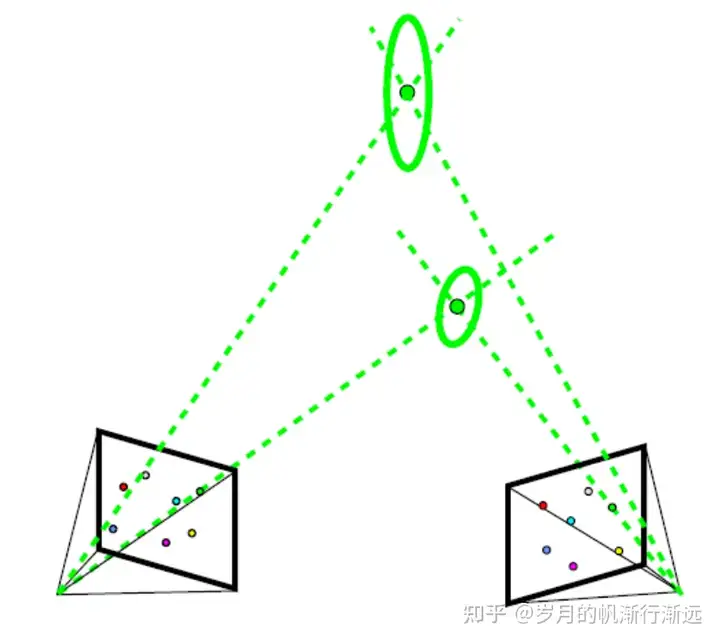
- 重投影误差比较大的点:

Tracks滤波
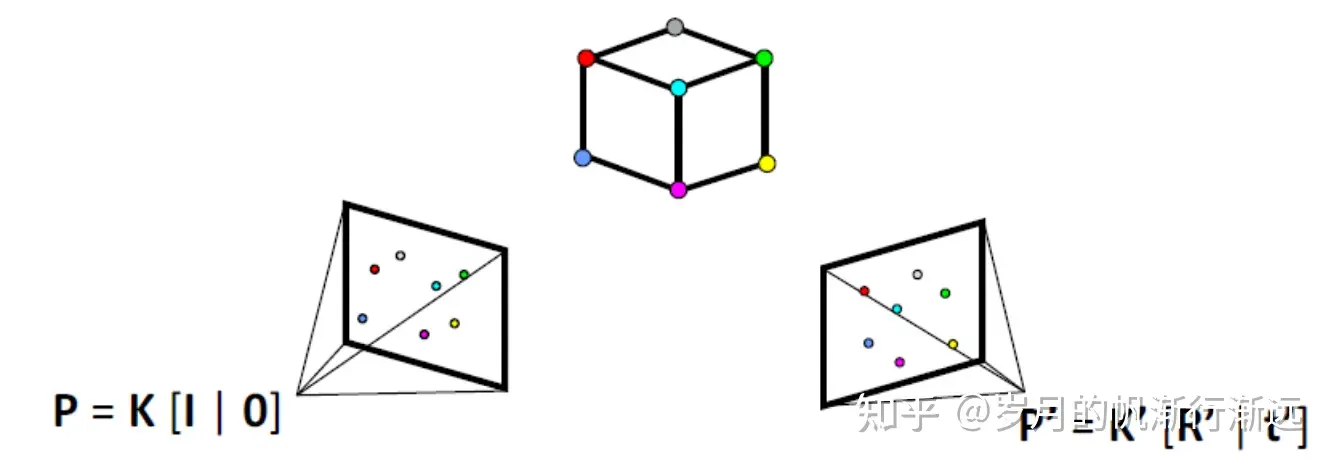
全局的捆绑调整
目前具有三维点和相机姿态的初始值。
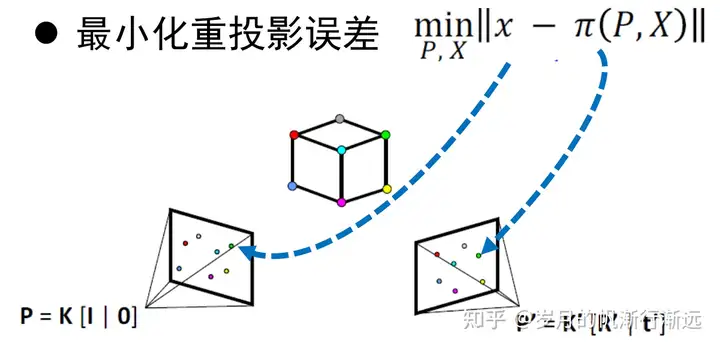
重建新的视角
- 选择新的视角
条件:可见的tracks数目最多。
将视角按照tracks由多到少进行排序。
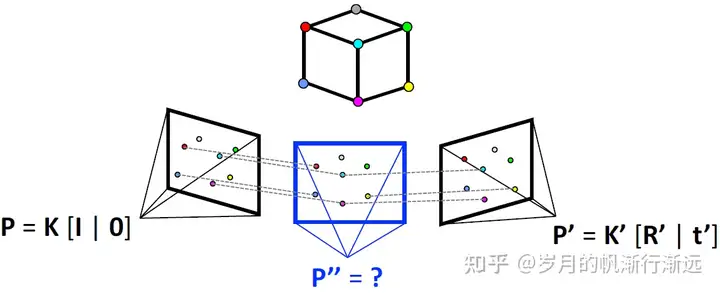
- 恢复新建相机的姿态
1 找到3D-2D对应关系;
2 用RANSAC-PnP算法求解相机姿态。
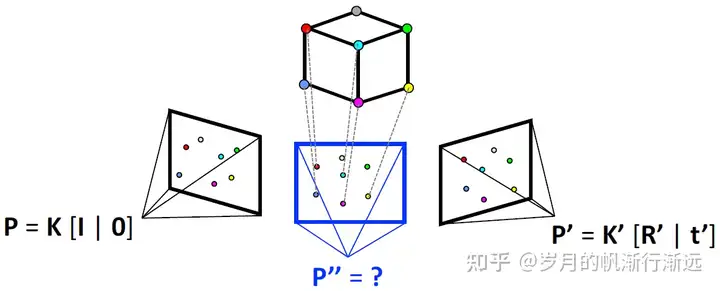
目前,已知三维点坐标以及这些点在新的像平面上的坐标,求解新的相机外参,这是一个PnP的问题。
每次采样三个点,得到相机姿态。把其他的点通过刚求出的相机姿态投影到像平面,计算重投影误差。通过误差找到内点,统计内点个数,不断采样,直到内点个数最多。最后使用这些内点求出相机姿态。
- 单个相机的捆绑调整
相机姿态的非线性优化
- Tracks重建
增加视角后,会产生新的tracks(有超过两个视角的匹配点)
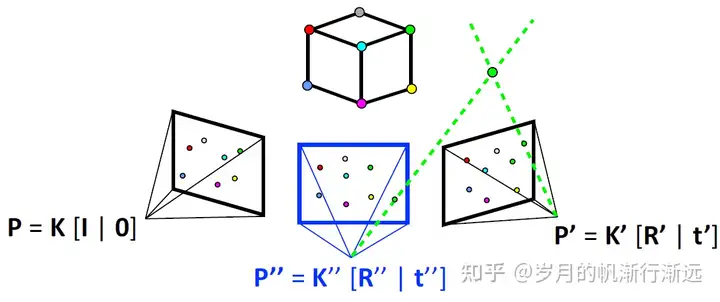
- Tracks滤波
重建后一定要进行滤波
- 全局的捆绑调整
增量捆绑调整的优缺点
优点:
- 对特征匹配外点鲁棒
- 重建精度高
- 捆绑调整不断优化场景结构
常用来做算法比较的基准
缺点:
- 对初始相机对的选取以及相机的添加顺序敏感
- 大场景产生累计误差导致场景漂移
- 重复进行捆绑调整,效率低
重建结果
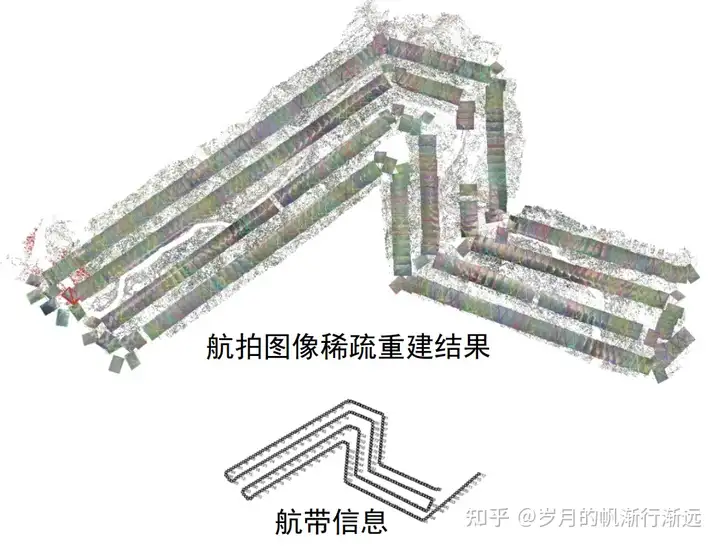
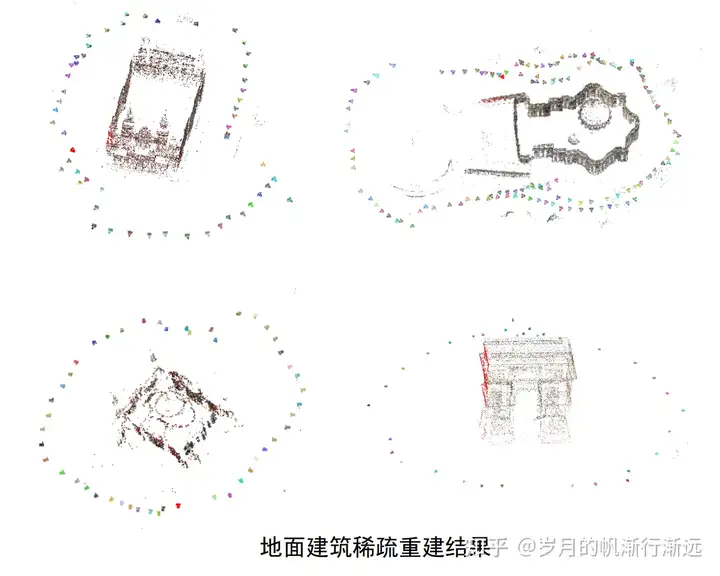
开源工具:
Bundler:增量的捆绑调整
VisualSFM:加速版本的增量SFM
Theia
Colmap
焦距的获取
径向畸变系数一般直接设置为0。
- 自标定的方法获取初始值,如VisualSFM
- 从可交换图像文件中读取EXIF初始值,如Bundler

尺度不确定性
没有实际的距离。点云中1mm不是实际中的1mm。点云的单位需要使用GPS进行地理标注,相机使用GPS得到真实的地理坐标。

动态物体
标准的SFM只能重建场景中的动态物体,对物体进行运动补偿。

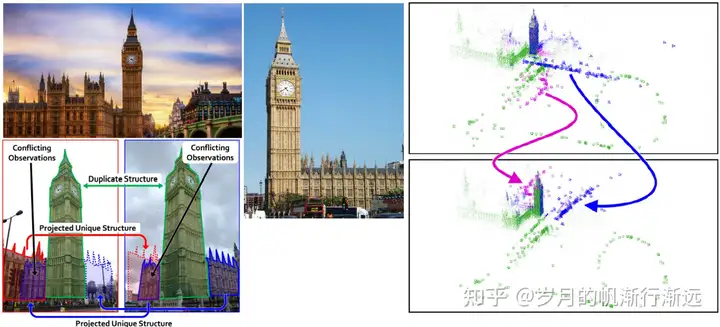
重复结构
由于描述子都是局部的,有很多的重复结构,会出现错误的匹配。
非朗伯面
朗伯面上的点朝每个方向的反射都是一样的。
而镜面或水面是非朗伯面,只在一个方向上的反射特别强,难以得到匹配点。
使用NCC的方法对局部的纹理进行匹配。
