首页 > 其他分享 >2023冲刺国赛模拟 4.1

2023冲刺国赛模拟 4.1

时间：2023-05-25 09:57:48浏览次数：45  
标签：4.1 int sum max1 国赛 len 2023 now mod

T1 宝石

需要统计每种方案中所含宝石的种类数之和，考虑对于每种宝石分开统计，设当前考虑了第 \(i\) 种宝石，容易发现只需要统计包含这种宝石的方案数，因为对每种宝石的方案数求和就是答案。包含的情况不好考虑，考虑求解不包含这种宝石的方案数，设包含这种宝石的节点构成集合 \(S\) ，容易发现这相当于在树上删去点集 \(S\) 后，选择 \(k\) 个节点使得 \(k\) 个节点联通。比较显然的思路是直接对包含这种宝石的节点建虚树做 dp ，复杂度 \(O(n\log n)\) 。

code 
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;

const int max1 = 5e5;
const int mod = 998244353;

int n, m, k, w[max1 + 5], id[max1 + 5];
vector <int> point[max1 + 5], edge[max1 + 5], sum[max1 + 5];

int inv[max1 + 5], fac[max1 + 5], ifac[max1 + 5];

int siz[max1 + 5], deep[max1 + 5], father[max1 + 5], son[max1 + 5];
int top[max1 + 5], dfn[max1 + 5], rk[max1 + 5], dfs_clock;

int tmp[max1 * 2 + 5], cnt;
int s[max1 + 5], stop;
vector <int> new_edge[max1 + 5];

int f[max1 + 5], ans;

int A ( int n, int m )
{
    if ( n < m )
        return 0;
    return 1LL * fac[n] * ifac[n - m] % mod;
}

void Find_Heavy_Edge ( int now, int fa, int depth )
{
    siz[now] = 1, deep[now] = depth, father[now] = fa, son[now] = 0;

    int max_siz = 0;
    for ( auto v : edge[now] )
    {
        if ( v == fa )
            continue;
        
        Find_Heavy_Edge(v, now, depth + 1);

        if ( max_siz < siz[v] )
            max_siz = siz[v], son[now] = v;
        siz[now] += siz[v];
    }
    return;
}

void Connect_Heavy_Edge ( int now, int ancestor )
{
    int num = 0;
    sum[now].push_back(0);

    dfn[now] = ++dfs_clock; rk[dfs_clock] = now; top[now] = ancestor;
    if ( son[now] )
    {
        Connect_Heavy_Edge(son[now], ancestor);
        id[son[now]] = ++num;
        sum[now].push_back(A(siz[son[now]], k));
    }
    
    for ( auto v : edge[now] )
    {
        if ( v == father[now] || v == son[now] )
            continue;
        
        Connect_Heavy_Edge(v, v);

        id[v] = ++num;
        sum[now].push_back(( sum[now].back() + A(siz[v], k) ) % mod);
    }
    return;
}

int Get_Lca ( int u, int v )
{
    while ( top[u] != top[v] )
    {
        if ( deep[top[u]] < deep[top[v]] )
            swap(u, v);
        
        u = father[top[u]];
    }

    if ( deep[u] > deep[v] )
        swap(u, v);
    
    return u;
}

int Kth_Ancestor ( int now, int k )
{
    while ( deep[now] - deep[top[now]] < k )
        k -= deep[now] - deep[top[now]] + 1, now = father[top[now]];
    return rk[dfn[now] - k];
}

void DP ( int now, int c )
{
    if ( w[now] == c )
    {
        int pre = 0;
        for ( auto v : new_edge[now] )
        {
            int p = Kth_Ancestor(v, deep[v] - deep[now] - 1);
            DP(v, c);
            
            ans = ( ans + ( sum[now][id[p] - 1] - sum[now][pre] + mod ) % mod ) % mod;
            pre = id[p];
   
            ans = ( ans + A(siz[p] - f[v], k) ) % mod;
        }

        ans = ( ans + ( sum[now].back() - sum[now][pre] + mod ) % mod ) % mod;

        f[now] = siz[now];
    }
    else
    {
        f[now] = 0;

        for ( auto v : new_edge[now] )
        {
            DP(v, c);

            f[now] += f[v];
        }
    }
    return;
}

void Solve ( int c )
{
    cnt = 0;
    for ( auto v : point[c] )
        tmp[++cnt] = dfn[v];
    sort(tmp + 1, tmp + 1 + cnt);

    int num = cnt - 1;
    for ( int i = 1; i <= num; i ++ )
        tmp[++cnt] = dfn[Get_Lca(rk[tmp[i]], rk[tmp[i + 1]])];
    tmp[++cnt] = dfn[n + 1];
    w[n + 1] = c;

    sort(tmp + 1, tmp + 1 + cnt);
    cnt = unique(tmp + 1, tmp + 1 + cnt) - ( tmp + 1 );
    for ( int i = 1; i <= cnt; i ++ )
    {
        tmp[i] = rk[tmp[i]];
        new_edge[tmp[i]].clear();
    }

    stop = 0;
    for ( int i = 1; i <= cnt; i ++ )
    {
        while ( stop && Get_Lca(s[stop], tmp[i]) != s[stop] )
            --stop;
        
        if ( s[stop] )
            new_edge[s[stop]].push_back(tmp[i]);
        
        s[++stop] = tmp[i];
    }

    DP(n + 1, c);

    return;
}

int main ()
{
    freopen("gem.in", "r", stdin);
    freopen("gem.out", "w", stdout);

    scanf("%d%d%d", &n, &m, &k);
    for ( int i = 1; i <= n; i ++ )
    {
        scanf("%d", &w[i]);
        point[w[i]].push_back(i);
    }
    for ( int i = 2, u, v; i <= n; i ++ )
    {
        scanf("%d%d", &u, &v);
        edge[u].push_back(v);
        edge[v].push_back(u);
    }

    edge[n + 1].push_back(1);
    edge[1].push_back(n + 1);

    inv[1] = 1;
    for ( int i = 2; i <= n; i ++ )
        inv[i] = 1LL * ( mod - mod / i ) * inv[mod % i] % mod;
    fac[0] = ifac[0] = 1;
    for ( int i = 1; i <= n; i ++ )
    {
        fac[i] = 1LL * fac[i - 1] * i % mod;
        ifac[i] = 1LL * ifac[i - 1] * inv[i] % mod;
    }

    Find_Heavy_Edge(n + 1, 0, 0);
    Connect_Heavy_Edge(n + 1, n + 1);

    for ( int i = 1; i <= m; i ++ )
    {
        if ( point[i].empty() )
            ans = ( ans + A(n, k) ) % mod;
        else
            Solve(i);
    }

    ans = ( 1LL * A(n, k) * m % mod - ans + mod ) % mod; 

    printf("%d\n", ans);

    return 0;
}

T2 序列

首先考虑 \(n\) 较小的情况，对于一次修改，我们维护数组 \(f\) 进行操作 \(f_{p_i}+x_i\to f_{p_i}\) ，容易发现最终的 \(a\) 序列满足 \(a_n=\sum_{d|n}\tfrac{n}{d}f_d\) ，这是狄利克雷前缀和的形式，考虑修改实际上是得到数组 \(g\) 满足 \(g_d=\sum_{d|n}\tfrac{n}{d}a_n\) ，这是狄利克雷后缀和的形式，因此我们可以在 \(O(n\log\log n)\) 的复杂度内求解答案。

正解考虑利用题目中的特殊性质，由于 \(p,k\) 的质因子集合 \(S\) 很小，在 \(1e9\) 的范围内只由这些质因子构成的数实际上也不超过 \(2e5\) ，因此考虑暴力 dfs 找出这些数，进行修改操作时，我们只保存 \(a\) 序列这些数位置上的值，对于一个位置 \(q\) ，如果 \(q\) 的质因子集合是 \(S\) 的子集，显然我们已经得到了这个位置在 \(a\) 序列上的值，如果 \(q\) 包含了除去 \(S\) 集合内以外的质因子，设 \(q=AB\) ，其中 \(A\) 中只包含 \(S\) 中的质因子， \(B\) 中不包含 \(S\) 中的质因子，考虑计算 \(a_q\) ：

\[\begin{aligned} a_q&=\sum_{i=1}^{m}[p_i|q]\tfrac{q}{p_i}x_i\\ &=\sum_{i=1}^{m}[p_i|q]\tfrac{AB}{p_i}x_i\\ &=B\sum_{i=1}^{m}[p_i|A]\tfrac{A}{p_i}x_i\\ &=Ba_A \end{aligned} \]

对于查询操作，由于每次询问的位置的质因子拆分一定为 \(S\) 的子集，因此我们只求解可以被 \(S\) 内质因子完全表示的位置 \(d\) 的值 \(g_d\) ：

\[\begin{aligned} g_d=&\sum_{d|n}\tfrac{n}{d}a_n\\ &=\sum_{d|AB}\tfrac{AB}{d}a_{AB}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (A\in S,B\not\in S)\\ &=\sum_{d|A}\sum_{A\times B\le n}\tfrac{AB}{d}a_{AB}\\ &=\sum_{d|A}\sum_{A\times B\le n}\tfrac{AB^2}{d}a_{A}\\ &=\sum_{d|A}\tfrac{A}{d}a_{A}\sum_{B=1}^{\lfloor\tfrac{n}{A}\rfloor}B^2[\gcd(B,S)=1]\\ &=\sum_{d|A}\tfrac{A}{d}a_{A}h(\lfloor\tfrac{n}{A}\rfloor) \end{aligned} \]

具体来讲，我们只求解可以被 \(S\) 内质因子完全表示的位置 \(d\) 处的 \(a_d\) ，之后令 \(a_dh(\lfloor\tfrac{n}{d}\rfloor)\to a_d\) ，只对这些位置做狄利克雷后缀和可以得到数组 \(g\) 。

简单提一下 \(h\) 的求解方法：

\[\begin{aligned} h(n)&=\sum_{i=1}^{n}[\gcd(i,S)=1]i^2\\ &=\sum_{i=1}^{n}\sum_{d|\gcd(i,S)}\mu(d)i^2\\ &=\sum_{d|S}\mu(d)d^2\sum_{i=1}^{\lfloor\tfrac{n}{d}\rfloor}i^2 \end{aligned} \]

因为 \(S\) 是一个集合，因此 \(\gcd(i,S)=1\) 的限制实际上是 \(i\) 不包含 \(S\) 内任意质因子，因此可以将 \(S\) 视为 \(\prod pr_i\) 。

code 
#include <cstdio>
#include <algorithm>
#include <unordered_map>
using namespace std;

const int max1 = 2e5, max2 = 10, max3 = 31622;
const int mod = 998244353;

int inv[10];

int n, m, q;
int p[max1 + 5], x[max1 + 5];
int k[max1 + 5];

int prime[max2 + 5], total;
int seq[max1 + 5], cnt;
unordered_map <int, int> f, g;

void Build ( int tmp )
{
    for ( int w = 1; w <= total; w ++ )
        while ( !( tmp % prime[w] ) )
            tmp /= prime[w];
    
    for ( int w = 2; w * w <= tmp; w ++ )
    {
        if ( !( tmp % w ) )
        {
            prime[++total] = w;
            while ( !( tmp % w ) )
                tmp /= w;
        }
    }

    if ( tmp != 1 )
        prime[++total] = tmp;

    return;
}

void Dfs ( int now, int v )
{
    if ( now == total + 1 )
        { seq[++cnt] = v; return; }

    for ( long long i = 1; 1LL * i * v <= n; i *= prime[now] )
        Dfs(now + 1, i * v);
    return;
}

int Sum ( int x )
{
    return 1LL * x * ( x + 1 ) % mod * ( x + x + 1 ) % mod * inv[6] % mod;
}

int Calc ( int x )
{
    if ( g.find(x) != g.end() )
        return g[x];
    
    int ans = 0;
    for ( int s = 0; s < 1 << total; s ++ )
    {
        long long d = 1;
        bool T = 0;
        for ( int i = 1; i <= total; i ++ )
        {
            if ( s >> i - 1 & 1 )
            {
                d *= prime[i];
                T ^= 1;
                if ( d > x )
                    break;
            }
        }

        if ( T )
            ans = ( ans - 1LL * Sum(x / d) * d % mod * d % mod + mod ) % mod;
        else
            ans = ( ans + 1LL * Sum(x / d) * d % mod * d % mod ) % mod;
    }

    return g[x] = ans;
}

int main ()
{
    freopen("sequence.in", "r", stdin);
    freopen("sequence.out", "w", stdout);

    inv[1] = 1;
    for ( int i = 2; i < 10; i ++ )
        inv[i] = 1LL * ( mod - mod / i ) * inv[mod % i] % mod;

    scanf("%d%d%d", &n, &m, &q);
    for ( int i = 1; i <= m; i ++ )
    {
        scanf("%d%d", &p[i], &x[i]);
        Build(p[i]);
    }
    for ( int i = 1; i <= q; i ++ )
    {
        scanf("%d", &k[i]);
        Build(k[i]);
    }

    sort(prime + 1, prime + 1 + total);

    Dfs(1, 1);
    sort(seq + 1, seq + 1 + cnt);

    for ( int i = 1; i <= m; i ++ )
        f[p[i]] = ( f[p[i]] + x[i] ) % mod;

    for ( int i = 1; i <= total; i ++ )
        for ( int j = 1; j <= cnt; j ++ )
            if ( 1LL * prime[i] * seq[j] <= n )
                f[prime[i] * seq[j]] = ( f[prime[i] * seq[j]] + 1LL * f[seq[j]] * prime[i] ) % mod;

    for ( int i = 1; i <= cnt; i ++ )
        f[seq[i]] = 1LL * f[seq[i]] * Calc(n / seq[i]) % mod;
    
    for ( int i = 1; i <= total; i ++ )
        for ( int j = cnt; j >= 1; j -- )
            if ( 1LL * prime[i] * seq[j] <= n )
                f[seq[j]] = ( f[seq[j]] + 1LL * f[prime[i] * seq[j]] * prime[i] ) % mod;
    
    for ( int i = 1; i <= q; i ++ )
        printf("%d\n", f[k[i]]);

    return 0;
}

T3 制胡窜

首先不存在任意两个相同的字符肯定无解，由于有解时一定存在两个相同的字符，因此答案最大为 \(4\) 。

考虑答案为 \(1\) 的情况，只需要判定子串为循环串，枚举区间长度的质因子作为循环次数，设循环长度为 \(len\) ，只需要判断 \(s_{l,r-len}=s_{l+len,r}\) 即可。

考虑答案为 \(2\) 的情况，不难发现此时子串形态由 \(AAB, BAA, ABA\) 三种情况，对于前两种情况，可以用 NOI2016 优秀的拆分中的方法求解。

具体的，考虑预处理数组 \(minR_i\) 表示以 \(i\) 为左端点，最小的满足 \(AA\) 串的右端点，同理预处理 \(maxL_i\) 表示以 \(i\) 为右端点，最大的满足 \(AA\) 串的左端点，考虑枚举 \(AA\) 串中 \(A\) 的长度进行求解，假设当前枚举的长度为 \(len\) ，我们在字符串 \(s\) 上每隔 \(len\) 的长度设置一个关键点，容易发现 \(A\) 长度为 \(len\) 的 \(AA\) 串一定经过其中两个关键点，因此考虑相邻的两个关键点的贡献，对于相邻的两个关键点 \(pre, i\) ，求解两点之间的 \(lcp\) 和 \(lcs\) ，如果 \(pre\) 的 \(lcp\) 与 \(i\) 的 \(lcs\) 长度之和 \(\ge len+1\) ，那么此时至少存在一个 \(AA\) 串经过关键点 \(i, pre\) ，具体来讲就是下面这张图：

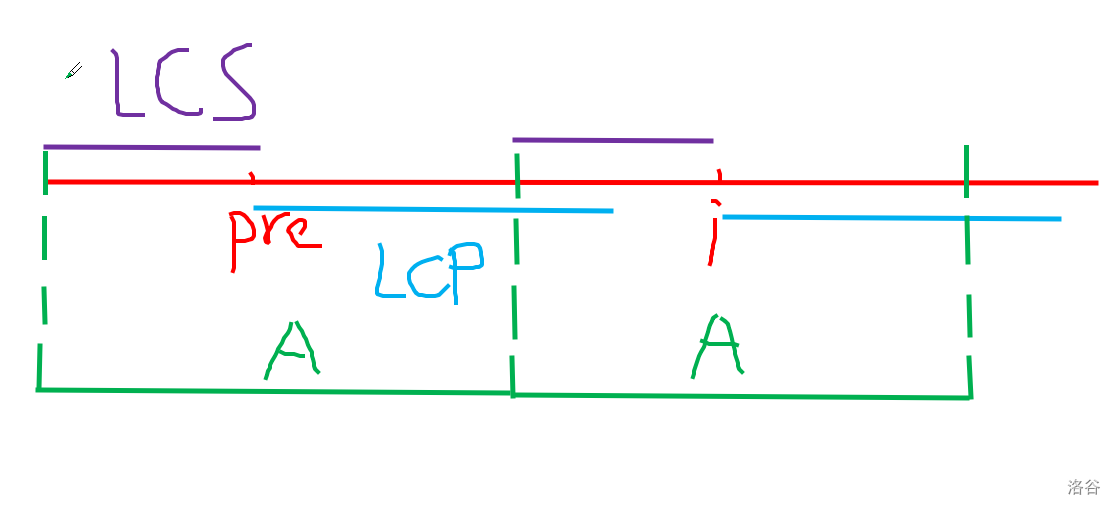
容易发现合法的 \(AA\) 串构成连续的一段，这相当于对 \(minR\) 数组的区间修改。

通过上述过程，可以在 \(O(n\log n)\) 的时间复杂度内得到 \(minR\) 和 \(maxL\) 。

考虑 \(ABA\) 的情况，实际上就是求解一个区间的最小 border ，考虑根号分治，对于 \(\le \sqrt{n}\) 的答案，我们直接暴力枚举，对于 \(>\sqrt{n}\) 的答案，假设此时存在一个长度 \(>\sqrt{n}\) 的最小 border ，那么这个 border 在整个字符串中的每次出现一定不会相交，如果相交那么一定存在更小的 border ，由于此时最小 border 长度 \(>\sqrt{n}\) ，因此这个 border 在整个字符串内出现次数不超过 \(\sqrt{n}\) 次，因此这个 border 的左端点与询问左端点 \(L\) 在后缀数组上的 rk 相差一定不超过 \(\sqrt{n}\) ，如果超过 \(\sqrt{n}\) ，那么这个 border 出现次数就会大于 \(\sqrt{n}\) ，与上述结论矛盾。

考虑答案为 \(3\) 的情况，只需要判断 \(aBaB, BaBa, ABBA\) 三种情况即可，前两种非常容易，第三种情况，由于我们已经得到了所有合法的 \(AA\) 串，那么此时的查询就是简单的二位数点，用 ST 表维护即可。

剩余情况答案为 \(4\) 。

code 
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <set>
#include <cmath>
#include <iostream>
using namespace std;

const int max1 = 2e5;

int n, m, B;
char s[max1 + 5];
int sum[max1 + 5][26];

int maxL[max1 + 5], minR[max1 + 5];

vector <int> add[max1 + 5], del[max1 + 5];
multiset <int> Set;

int prime[max1 + 5], total;
bool is_not_prime[max1 + 5];
vector <int> d[max1 + 5];

void Get_Prime ()
{
    for ( int i = 2; i <= n; i ++ )
    {
        if ( !is_not_prime[i] )
            prime[++total] = i;
        for ( int j = 1; j <= total && i * prime[j] <= n; j ++ )
        {
            int k = i * prime[j];
            is_not_prime[k] = true;
            if ( !( i % prime[j] ) )
                break;
        }
    }

    for ( int i = 1; i <= total; i ++ )
        for ( int k = prime[i]; k <= n; k += prime[i] )
            d[k].push_back(prime[i]);

    return;
}

struct Suffix_Array
{
    int x[max1 + 5], y[max1 + 5], bin[max1 + 5], lim;
    int sa[max1 + 5], rk[max1 + 5], height[max1 + 5];
    
    int list[max1 + 5][20];

    void Build ( const int *A )
    {
        for ( int i = 1; i <= n; i ++ )
            list[i][0] = A[i];
        for ( int k = 1; ( 1 << k ) <= n; k ++ )
            for ( int i = 1; i + ( 1 << k ) - 1 <= n; i ++ )
                list[i][k] = min(list[i][k - 1], list[i + ( 1 << k - 1 )][k - 1]);
        return;
    }

    int Query ( int L, int R )
    {
        if ( L == R )
            return n - L + 1;
        L = rk[L], R = rk[R];
        if ( L > R )
            swap(L, R);
        ++L;
        return min(list[L][__lg(R - L + 1)], list[R - ( 1 << __lg(R - L + 1) ) + 1][__lg(R - L + 1)]);
    }

    void Build ()
    {
        lim = 'z';
        memset(bin, 0, sizeof(int) * ( lim + 1 ));
        for ( int i = 1; i <= n; i ++ )
            x[i] = s[i];
        for ( int i = 1; i <= n; i ++ )
            ++bin[x[i]];
        for ( int i = 1; i <= lim; i ++ )
            bin[i] += bin[i - 1];
        for ( int i = n; i >= 1; i -- )
            sa[bin[x[i]]--] = i;
        
        for ( int w = 1; w <= n; w <<= 1 )
        {
            int num = 0;
            for ( int i = n - w + 1; i <= n; i ++ )
                y[++num] = i;
            for ( int i = 1; i <= n; i ++ )
                if ( sa[i] > w )
                    y[++num] = sa[i] - w;
            
            memset(bin, 0, sizeof(int) * ( lim + 1 ));
            for ( int i = 1; i <= n; i ++ )
                ++bin[x[i]];
            for ( int i = 1; i <= lim; i ++ )
                bin[i] += bin[i - 1];
            for ( int i = n; i >= 1; i -- )
                sa[bin[x[y[i]]]--] = y[i];
            
            memcpy(y + 1, x + 1, sizeof(int) * n);
            
            x[sa[1]] = lim = 1;
            for ( int i = 2; i <= n; i ++ )
            {
                if ( y[sa[i - 1]] == y[sa[i]] && y[sa[i - 1] + w] == y[sa[i] + w] )
                    x[sa[i]] = lim;
                else
                    x[sa[i]] = ++lim;
            }

            if ( lim == n )
                break;
        }

        for ( int i = 1; i <= n; i ++ )
            rk[sa[i]] = i;
        for ( int i = 1; i <= n; i ++ )
        {
            if ( rk[i] == 1 )
                height[rk[i]] = 0;
            else
            {
                int k = height[rk[i - 1]];
                if ( k )
                    --k;
                while ( i + k <= n && sa[rk[i] - 1] + k <= n && s[i + k] == s[sa[rk[i] - 1] + k] )
                    ++k;
                
                height[rk[i]] = k;
            }
        }

        Build(height);

        return;
    }

}SA1, SA2;

struct ST_List
{
    int list[max1 + 5][20];
    
    void Build ( const int *A )
    {
        for ( int i = 1; i <= n; i ++ )
            list[i][0] = A[i];
        for ( int k = 1; ( 1 << k ) <= n; k ++ )
            for ( int i = 1; i + ( 1 << k ) - 1 <= n; i ++ )
                list[i][k] = min(list[i][k - 1], list[i + ( 1 << k - 1 )][k - 1]);
        return;
    }

    int Query ( int L, int R )
    {
        return min(list[L][__lg(R - L + 1)], list[R - ( 1 << __lg(R - L + 1) ) + 1][__lg(R - L + 1)]);
    }
}ST;

int LCP ( int i, int j )
{
    return SA1.Query(i, j);
}

int LCS ( int i, int j )
{
    return SA2.Query(n - i + 1, n - j + 1);
}

void Solve ()
{
    int L, R;
    scanf("%d%d", &L, &R);
    int cnt = 0;
    for ( int i = 0; i < 26; i ++ )
        cnt += sum[R][i] - sum[L - 1][i] > 1;

    if ( !cnt )
        { printf("-1\n"); return; }
    
    cnt = 0;
    for ( int i = 0; i < 26; i ++ )
        cnt += sum[R][i] - sum[L - 1][i] > 0;
    
    if ( cnt == 1 )
        { printf("1\n"); return; }
    
    for ( auto p : d[R - L + 1] )
    {
        int len = ( R - L + 1 ) / p;
        if ( len != R - L + 1 && LCP(L, L + len) >= R - L + 1 - len )
            { printf("1\n"); return; }
    }
    
    if ( minR[L] <= R )
        { printf("2\n"); return; }
    if ( maxL[R] >= L )
        { printf("2\n"); return; }
    
    for ( int i = 1; i <= min(B, R - L); i ++ )
        if ( LCP(L, R - i + 1) >= i )
            { printf("2\n"); return; }
    
    for ( int i = max(1, SA1.rk[L] - B); i <= min(n, SA1.rk[L] + B); i ++ )
    {
        if ( SA1.sa[i] <= L || SA1.sa[i] > R )
            continue;

        int match = LCP(L, SA1.sa[i]), p = R - SA1.sa[i] + 1;
        if ( match >= p && L + p <= SA1.sa[i] )
            { printf("2\n"); return; }
    }

    if ( sum[R][s[L] - 'a'] - sum[L - 1][s[L] - 'a'] > 1 || sum[R][s[R] - 'a'] - sum[L - 1][s[R] - 'a'] > 1 )
        { printf("3\n"); return; }
    
    if ( ST.Query(L, R) <= R )
        { printf("3\n"); return; }
    
    printf("4\n");
    return;
}

int main ()
{
    freopen("string.in", "r", stdin);
    freopen("string.out", "w", stdout);

    scanf("%d%s", &n, s + 1); B = sqrt(n); Get_Prime();

    for ( int i = 1; i <= n; i ++ )
        for ( int j = 0; j < 26; j ++ )
            sum[i][j] = sum[i - 1][j] + ( s[i] == 'a' + j );

    SA1.Build(); reverse(s + 1, s + 1 + n);
    SA2.Build(); reverse(s + 1, s + 1 + n);

    for ( int i = 1; i <= n; i ++ )
        maxL[i] = 0, minR[i] = n + 1;
    
    for ( int i = 1; i <= n; i ++ )
        add[i].clear(), del[i].clear();

    for ( int len = 1; len <= n; len ++ )
    {
        for ( int i = len + 1; i <= n; i += len )
        {
            int pre = i - len;
            if ( s[pre] == s[i] )
            {
                int lcp = LCP(pre, i), lcs = LCS(pre, i);

                if ( lcp + lcs >= len + 1 )
                {
                    add[pre - lcs + 1].push_back(len + len);
                    del[pre + lcp - len + 1].push_back(len + len);
                }
            }
        }
    }

    Set.clear();

    for ( int i = 1; i <= n; i ++ )
    {
        for ( auto v : add[i] )
            Set.insert(v);
        for ( auto v : del[i] )
            Set.erase(Set.find(v));
        
        if ( !Set.empty() )
            minR[i] = i + ( *Set.begin() ) - 1;
    }

    for ( int i = 1; i <= n; i ++ )
        add[i].clear(), del[i].clear();
    
    for ( int len = 1; len <= n; len ++ )
    {
        for ( int i = len + 1; i <= n; i += len )
        {
            int pre = i - len;
            if ( s[pre] == s[i] )
            {
                int lcp = LCP(pre, i), lcs = LCS(pre, i);

                if ( lcp + lcs >= len + 1 )
                {
                    add[i + lcp - 1].push_back(len + len);
                    del[i - lcs + len - 1].push_back(len + len);
                }
            }
        }
    }

    Set.clear();

    for ( int i = n; i >= 1; i -- )
    {
        for ( auto v : add[i] )
            Set.insert(v);
        for ( auto v : del[i] )
            Set.erase(Set.find(v));
        
        if ( !Set.empty() )
            maxL[i] = i - ( *Set.begin() ) + 1;
    }

    ST.Build(minR);

    scanf("%d", &m);
    while ( m -- )
        Solve();

    return 0;
}

标签：4.1,int,sum,max1,国赛,len,2023,now,mod
From： https://www.cnblogs.com/KafuuChinocpp/p/17430271.html

相关文章

  • Microsoft Build 云技能挑战 2023：免费认证考试
    参加MicrosoftBuild并完成MicrosoftBuild云技能挑战。按照条款及条件，通过完成MicrosoftLearn上的八个独特集合之一，提高、扩展和发现新技能并获得免费认证考试。挑战将持续到6月20日，因此请立即注册并开始，以避免错失机会。以帮助你持续提升技能，并向你的雇主和同事证明......
  • SSO2.0 9-20230524
              ......
  • PMP-4.10 规划相关方参与
    ##############################################################规划相关方参与是规划过程组的最后一章内容。其实相关方管理从项目最开始就已经在进行，只不过，对于一般项目而言，无需详细列出进行分析。而且相关方的信息，大部分在销售手中，他会对不同的相关方有粗劣的判断和认定，但......
  • 2023-5-24
    忙碌结束的结束了两个ddl，看完了《刑事ZERO》嗯，，忘了还有啥评价是还算快乐评价是德语难念（虽然就是个书名未结束的后面要处理的事情大概就是人工智能，机器人和GameJam（中间一个CSP应该做点别的事情了，这两天《夜の向日葵》也练到了难点发现口琴还是需要下功夫练的看《LegalHi......
  • 2023 (ICPC) Jiangxi Provincial Contest -- Official Contest
    2023(ICPC)JiangxiProvincialContest--OfficialContest A-DrillWoodtoMakeFire思路：n>=s*vB-WonderfulArray思路：对a进行a%m，不会对结果造成影响，则0<=bi+1-bi<m。可以求bi+1%m<bi%m的个数，等价于bi+1/m>bi/m，整体来看，就是求bn/m#include<bits/stdc++.h>using......
  • 2023/5/24每日随笔 项目基本实现
    今天，上了几节课，然后进行项目的完善与基本实现一：实现了调用相册，将地址提取二：实现了图片提取加分类三：实现了添加后更新四：结果展示五：项目问题以及可能出现bug一：实现了调用相册，将地址提取具体更改的这个方法：完整代码来自《第一行代码》调用相册和使用相机。更改后调用的相册可......
  • 2023.5.24
     1#include<iostream>2#include<iomanip>3usingnamespacestd;4classHorse5{6public:7Horse()8{9cout<<"Horse申请了空间..."<<endl;10}11virtual~Horse()12{13......
  • 2022-2023年的jlu.test，和校园网出口的流量备忘
    2022年8月疫情结束，学生开学，jlu.test流量升高；2023年12月疫情放开，学生提前离校流量下降；2023年2月学生开始返校；2023年4月末除了南岭校区，其他校区的流量都切换到本地。2022年下半年的几次封校，流量出现陡增。今年流量比较正常，5月1日放假，流量下降不少。     20220325出......
  • 2023.5 路桥中学高一期末程序素养检测
    参考答案（个人编写）Aa,b=map(int,input().split())c=int(input())print(c-a+b)Ba=float(input())print("%.2lf"%(a*9/5+32))Ca=float(input())ifa>3:a=int(a)print(((a+1-3)*2+10))else:print(10)Da......
  • 2023.5.24每日总结
    <%@pagelanguage="java"contentType="text/html;charset=UTF-8"pageEncoding="UTF-8"%><!DOCTYPEhtmlPUBLIC"-//W3C//DTDHTML4.01Transitional//EN""http://www.w3.org/TR/html4/loose.dtd"&g......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99