[HAOI2018]字串覆盖
题目描述
小C对字符串颇有研究,他觉得传统的字符串匹配太无聊了,于是他想到了这
样一个问题.
对于两个长度为n的串A, B, 小C每次会给出给出4个参数s, t, l, r. 令A从s到t的
子串(从1开始标号)为T,令B从l到r的子串为P.然后他会进行下面的操作:
如果T的某个子串与P相同,我们就可以删掉T的这个子串,并获得K − i的收
益,其中i是初始时A中(注意不是T中)这个子串的起始位置,K是给定的参数.
删除操作可以进行任意多次,你需要输出获得收益的最大值.
注意每次询问都是独立的,即进行一次询问后,删掉的位置会复原.
输入格式
从文件cover.in中读入数据.
第一行两个整数n, K,表示字符串长度和参数.
接下来一行一个字符串A.
接下来一行一个字符串B.
接下来一行一个整数q,表示询问个数.
接下来q行,每行四个整数s, t, l, r,表示一次询问.
输出格式
输出到文件cover.out中.
输出q行,每行一个整数,表示一个询问的答案.
样例 #1
样例输入 #1
10 11
abcbababab
ababcbabab
5
1 9 7 9
3 10 8 10
1 10 1 2
5 7 2 3
1 5 3 6
样例输出 #1
6
10
22
5
10
提示
样例1解释 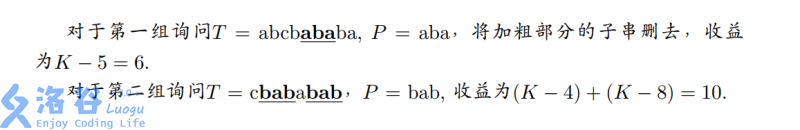
子任务
对于所有数据,有 $ 1 ≤ n, q ≤ 10^5 $ ,A, B仅由小写英文字母组成,$ 1 ≤ s ≤ t ≤n $ , $ 1 ≤ l ≤ r ≤ n $ , $ n < K ≤ 10^9 $ .
HAOI2018 round1 T3
对于 $ n = 10^5 $ 的测试点,满足\(51≤r−l≤2*10^3\) 的询问不超过11000个,且r−l在该区间内均匀随机
作为一道省选压轴题,这题还是偏简单的。
有一个很显然的贪心:一定是尽量地往前选,选越多越好。因为 \(k>n\),同时选的 \(k-i\) 中 \(i\) 一定是越小越好。
见到这个数据范围,明显要求我们分类分成 \(r-l>50\) 和 \(r-l\le 50\) 来处理
\(r-l>50\) 的方法就非常板子了。容易发现当 \(r-l>2000\) 的时候,选的串的个数一定不超过 $|S|\div(r-l)\le50 $,这就变成了一个字符串题。对S 建 SAM 后,找到 T[l...r] 所对应的等价类。怎么找等价类呢?可以建SAM 时把两个串连在一起建,然后在两个串中间放一些特殊字符,然后只要找到 \(T\) 对应的等价类就可以了。可以在 SAM 上用线段树合并维护等价类出现位置,然后每次线段树二分出下一个选的地方在哪就行了。而在 \(51\le r-l\le 2000\) 时,串的个数不超过 \(|S|\div r-l\le 2000\),同时询问还只有 \(11000\) 次,带个 log 3s 还是跑的过去的。
当 \(r-l\le 50\) 的时候,考虑把所有串给找出来跑。枚举所有长度不超过 50 的串,然后把那些一样的给找出来。对于每个询问,可以用倍增去统计就行了。
#include<bits/stdc++.h>
#define vit vector<int>::iterator
using namespace std;
typedef long long LL;
const int N=1e5+5,INF=2e9;
int k,n,TME,tme,nx[N][20];
LL ans[N],ns[N][20];
char s[N],t[N];
vector<int>p[51],q[N<<2],g[N];
string str;
map<string,int>mp;
struct query{
int l,r,s,t,id;
}qu[N];
template<int N>struct segment{
int tr[N],lc[N],rc[N],idx;
void update(int&o,int l,int r,int x)
{
if(!o)
o=++idx;
if(l==r)
return;
int md=l+r>>1;
if(md>=x)
update(lc[o],l,md,x);
else
update(rc[o],md+1,r,x);
}
int merge(int p,int q)
{
if(!p||!q)
return p|q;
lc[p]=merge(lc[p],lc[q]);
rc[p]=merge(rc[p],rc[q]);
return p;
}
int erfen(int o,int l,int r,int x)
{
if(!o)
return INF;
if(x>r)
return INF;
if(l==r)
return l;
int md=l+r>>1,k;
if((k=erfen(lc[o],l,md,x))^INF)
return k;
return erfen(rc[o],md+1,r,x);
}
};
template<int N,int M> struct graph{
struct edge{
int v,nxt;
}e[M];
int hd[N],e_num;
void add_edge(int u,int v)
{
e[++e_num]=(edge){v,hd[u]};
hd[u]=e_num;
}
};
template<int N>struct SAM{
int tr[N<<1][27],l[N<<1],fil[N<<1][21],idx=1,ls=1,g[N],rt[N<<1];
segment<N*60> s;
graph<N<<1,N<<1>t;
void insert(int s)
{
int k=++idx,p=ls;
g[l[k]=l[ls]+1]=k,ls=k;
SAM::s.update(rt[k],1,2*n+1,l[k]);
while(p&&!tr[p][s])
tr[p][s]=k,p=fil[p][0];
if(!p)
fil[k][0]=1;
else
{
int q=tr[p][s];
if(l[q]==l[p]+1)
fil[k][0]=q;
else
{
int nw=++idx;
l[nw]=l[p]+1,fil[nw][0]=fil[q][0];
memcpy(tr[nw],tr[q],sizeof(tr[0]));
fil[q][0]=fil[k][0]=nw;
while(p&&tr[p][s]==q)
tr[p][s]=nw,p=fil[p][0];
}
}
}
void dfs(int x)
{
for(int i=1;i<=20;i++)
fil[x][i]=fil[fil[x][i-1]][i-1];
for(int i=t.hd[x];i;i=t.e[i].nxt)
dfs(t.e[i].v);
}
void build()
{
for(int i=2;i<=idx;i++)
t.add_edge(fil[i][0],i);
dfs(1);
}
void sou(int x)
{
for(int i=t.hd[x];i;i=t.e[i].nxt)
{
sou(t.e[i].v);
rt[x]=s.merge(rt[x],rt[t.e[i].v]);
}
for(int i=0;i<q[x].size();i++)
{
int len=qu[q[x][i]].r-qu[q[x][i]].l,lst=qu[q[x][i]].s+len,c=0;
LL sum=0;
while(1)
{
int k=s.erfen(rt[x],1,n+n+1,lst);
if(k>qu[q[x][i]].t)
break;
sum+=k-len,++c;
lst=k+len+1;
}
ans[q[x][i]]=1LL*c*k-sum;
}
}
void add(int r,int len,int x)
{
int k=g[r];
for(int i=20;i>=0;i--)
if(l[fil[k][i]]>=len)
k=fil[k][i];
q[k].push_back(x);
}
};
SAM<N<<1>sm;
int main()
{
scanf("%d%d%s%s%d",&n,&k,s+1,t+1,&TME);
for(int i=1;i<=n;i++)
sm.insert(s[i]-'a');
sm.insert(26);
for(int i=1;i<=n;i++)
sm.insert(t[i]-'a');
sm.build();
for(int i=1;i<=TME;i++)
{
scanf("%d%d%d%d",&qu[i].s,&qu[i].t,&qu[i].l,&qu[i].r);
qu[i].id=i;
if(qu[i].r-qu[i].l<=50)
p[qu[i].r-qu[i].l].push_back(i);
else
sm.add(n+1+qu[i].r,qu[i].r-qu[i].l+1,i);
}
for(int i=0;i<=50;i++)
{
for(int i=1;i<=tme;i++)
g[i].clear();
tme=0;
mp.clear();
for(int j=1;j+i<=n;j++)
{
str="";
for(int k=j;k<=j+i;k++)
str.push_back(s[k]);
if(!mp[str])
mp[str]=++tme;
g[mp[str]].push_back(j);
}
for(int i=0;i<=n+1;i++)
for(int j=0;j<20;j++)
nx[i][j]=n+1,ns[i][j]=0;
for(int j=1;j<=tme;j++)
{
for(int k=0;k<g[j].size();k++)
{
vector<int>::iterator it=upper_bound(g[j].begin(),g[j].end(),g[j][k]+i);
if(it!=g[j].end())
ns[g[j][k]][0]=nx[g[j][k]][0]=*it;
}
}
for(int i=n;i>=0;i--)
for(int j=1;j<20;j++)
ns[i][j]=ns[i][j-1]+ns[nx[i][j-1]][j-1],nx[i][j]=nx[nx[i][j-1]][j-1];
for(int j=0;j<p[i].size();j++)
{
str="";
for(int k=qu[p[i][j]].l;k<=qu[p[i][j]].r;k++)
str.push_back(t[k]);
if(mp[str])
{
int k=mp[str];
vit it=lower_bound(g[k].begin(),g[k].end(),qu[p[i][j]].s);
if(it!=g[k].end()&&(*it)+i<=qu[p[i][j]].t)
{
int nw=*it,ret=1;
LL s=nw;
for(int k=19;k>=0;k--)
if(nx[nw][k]+i<=qu[p[i][j]].t)
ret+=1<<k,s+=ns[nw][k],nw=nx[nw][k];
ans[p[i][j]]=1LL*ret*::k-s;
}
}
}
}
sm.sou(1);
for(int i=1;i<=TME;i++)
printf("%lld\n",ans[i]);
return 0;
}