T1 fun
\(\sum_{B}\prod_{i=1}^n\binom{B_i}{A_i}\) ,设 \(B\) 序列的长度为 \(T\) ,考虑这个式子的组合意义,首先枚举 \(B\) 是将长度为 \(T\) 的序列划分为 \(n\) 段, \(\binom{B_i}{A_i}\) 是在第 \(i\) 段内选出 \(A_i\) 个位置,考虑简化这个选择的过程,在原序列中加入 \(n-1\) 个位置,上述过程可以被认为在长度为 \(T+n-1\) 的序列中选择 \(\sum_{i}A_i+n-1\) 个位置,其中第 \(\sum_{j=1}^iA_j+i\) 个位置表示原序列的划分,剩余位置为在每段划分中选择 \(A_i\) 个位置的方案,因此上述式子为:
\[\binom{T+n-1}{\sum A_i+n-1} \]那么答案为 \(\sum_{T\le M}\binom{T+n-1}{\sum A_i+n-1}\)
仍然用组合意义优化,在总长为 \(M+n-1\) 的序列后加入一个位置,之后在整个序列中选择 \(\sum A_i+n\) 个位置,最后一个位置为终止标记,因此答案实际上为 \(\binom{M+n}{\sum A_i+n}\) 。
当然,很容易发现上述式子可以拉格朗日插值计算,因此可以无脑暴算,复杂度仍然是 \(O(\sum A_i)\) 。
code
#include <cstdio>
using namespace std;
const int max1 = 2010;
const int mod = 1e9 + 7;
int n, m, A[max1 + 5], sum;
int inv[max1 * max1 + 5], ifac[max1 * max1 + 5], y[max1 * max1 + 5];
int Lprod[max1 * max1 + 5], Rprod[max1 * max1 + 5];
void Add ( int &x, int y )
{
x = x + y;
if ( x >= mod )
x = x - mod;
return;
}
int Lagrange ( int x, int p )
{
if ( x <= p )
return y[x];
Lprod[0] = x;
for ( int i = 1; i <= p; i ++ )
Lprod[i] = 1LL * Lprod[i - 1] * ( x - i ) % mod;
Rprod[p] = x - p;
for ( int i = p - 1; i >= 0; i -- )
Rprod[i] = 1LL * Rprod[i + 1] * ( x - i ) % mod;
int res = 0;
for ( int i = 0; i <= p; i ++ )
{
int up = 1;
if ( i > 0 )
up = 1LL * up * Lprod[i - 1] % mod;
if ( i < p )
up = 1LL * up * Rprod[i + 1] % mod;
up = 1LL * up * ifac[i] % mod;
up = 1LL * up * ifac[p - i] % mod;
if ( p - i & 1 )
up = ( mod - up ) % mod;
up = 1LL * up * y[i] % mod;
res = ( res + up ) % mod;
}
return res;
}
int main ()
{
scanf("%d%d", &n, &m);
for ( int i = 1; i <= n; i ++ )
scanf("%d", &A[i]), sum += A[i];
if ( m < sum )
printf("0\n");
else
{
sum += n - 1;
inv[1] = 1;
for ( int i = 2; i <= sum + 5; i ++ )
inv[i] = 1LL * ( mod - mod / i ) * inv[mod % i] % mod;
ifac[0] = inv[1];
for ( int i = 1; i <= sum + 5; i ++ )
ifac[i] = 1LL * ifac[i - 1] * inv[i] % mod;
int base = 1;
for ( int i = 1; i <= sum - 1; i ++ )
base = 1LL * base * i % mod;
for ( int i = 0; i <= sum + 5; i ++ )
{
base = 1LL * base * ( sum + i ) % mod;
y[i] = 1LL * base * ifac[i] % mod * ifac[sum] % mod;
}
for ( int i = 1; i <= sum + 5; i ++ )
Add(y[i], y[i - 1]);
printf("%d\n", Lagrange(m - sum + n - 1, sum + 5));
}
return 0;
}
T2 tree
考虑利用树的直径解决本题。
设树的一条直径为 \(u,v\) ,当 \(u,v\) 节点同色时,所有方案的贡献就是 \(\operatorname{dis}(u,v)\) ,这很容易统计,因此只考虑 \(u,v\) 节点异色的情况,设 \(f_i\) 表示贡献 \(\ge i\) 的方案数,考虑一个节点 \(p\) 的贡献,由于此时直径端点异色,因此当前节点颜色一定与直径上某点颜色相同,因此该点最大的贡献为 \(\max(\operatorname{dis}(u,p),\operatorname{dis}(v,p))\) ,最小贡献为 \(\min(\operatorname{dis}(u,p),\operatorname{dis}(v,p))\) ,设 \(lim=\min_i(\operatorname{dis}(u,i),\operatorname{dis}(v,i))\) ,那么对于 \(i\le lim\) , \(f_i=\) 总方案数,对于 \(i>lim\) ,考虑计算不合法的方案,也就是所有点的贡献均 \(<i\) 的方案数,统计 \(\max(\operatorname{dis}(u,p),\operatorname{dis}(v,p))\ge i\) 的点的数量,这些点选择的方案显然只有一种,由于 \(\min(\operatorname{dis}(u,p),\operatorname{dis}(v,p))\le\tfrac{\operatorname{dis}(u,v)}{2}\) ,可以发现直径中心划分开的若干连通块内所有确定点决策相同,因此这些确定的点之间的距离不会超过 \(i\) ,而剩余点最大的贡献为 \(\max(\operatorname{dis}(u,p),\operatorname{dis}(v,p))\) ,这个值不超过 \(i\) ,因此决策任意。
code
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int max1 = 1e6;
const int mod = 1e9 + 7;
int n;
vector <int> edge[max1 + 5];
int deep[2][max1 + 5];
int power[max1 + 5], bin[max1 + 5], ans;
void Dfs ( int now, int fa, int id, int depth )
{
deep[id][now] = depth;
for ( auto v : edge[now] )
{
if ( v == fa )
continue;
Dfs(v, now, id, depth + 1);
}
return;
}
int main ()
{
scanf("%d", &n);
for ( int i = 2, u; i <= n; i ++ )
{
scanf("%d", &u);
edge[u].push_back(i);
edge[i].push_back(u);
}
int p1, p2;
Dfs(1, 0, 0, 0);
p1 = 1;
for ( int i = 1; i <= n; i ++ )
if ( deep[0][i] > deep[0][p1] )
p1 = i;
Dfs(p1, 0, 0, 0);
p2 = p1;
for ( int i = 1; i <= n; i ++ )
if ( deep[0][i] > deep[0][p2] )
p2 = i;
Dfs(p2, 0, 1, 0);
power[0] = 1;
for ( int i = 1; i <= n; i ++ )
power[i] = ( power[i - 1] + power[i - 1] ) % mod;
ans = 1LL * power[n - 1] * deep[0][p2] % mod;
int lim = 0;
for ( int i = 1; i <= n; i ++ )
if ( i != p1 && i != p2 )
lim = max(lim, min(deep[0][i], deep[1][i]));
for ( int i = 1; i <= lim; i ++ )
ans = ( ans + power[n - 1] ) % mod;
for ( int i = 1; i <= n; i ++ )
if ( i != p1 && i != p2 )
++bin[max(deep[0][i], deep[1][i])];
for ( int i = n; i >= 1; i -- )
bin[i] += bin[i + 1];
for ( int i = lim + 1; i <= n; i ++ )
ans = ( ans + ( power[n - 1] - power[n - 1 - bin[i]] + mod ) % mod ) % mod;
printf("%d\n", ans);
return 0;
}
T3 work
很容易猜到做法为网络流,考虑进行建模。
每个人存在同意和不同意两种状态,每个组存在是否合作两种状态,设网络流源点为 \(S\) ,汇点为 \(T\) ,一个大体的思路是割掉与 \(S\) 相邻的边表示同意,割掉与 \(T\) 相邻的边表示不同意,具体的来讲,考虑一组 \(i,i+1\) ,从 \(S\) 向 \(i,i+1\) 连接流量为 \(d_i,d_{i+1}\) 的边,建立虚点 \(x\) 表示合作关系,从 \(i,i+1\) 分别向 \(x\) 连接流量为 \(c_i,c_{i+1}\) 的边,从 \(x\) 向 \(T\) 连接流量为 \(c_i+c_{i+1}\) 的边,从 \(i\) 向 \(i+1\) 连接流量为 \(e_i\) 的边,从 \(i+1\) 向 \(i\) 连接流量为 \(e_{i+1}\) 的边。
考虑这样做的含义,此时存在 \(5\) 种割流的方法。
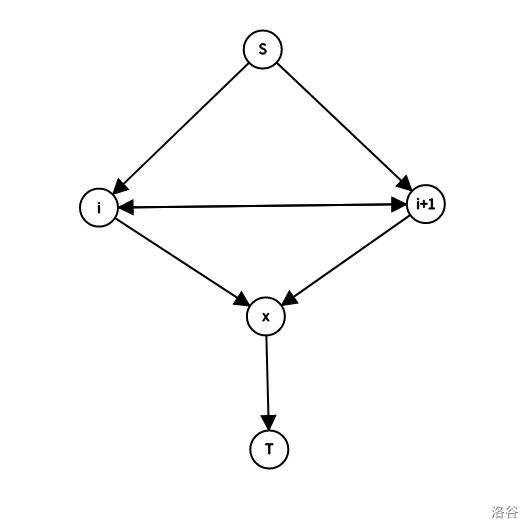
-
割掉 \(S\to i,S\to i+1\) 表示均不同意;
-
割掉 \(i\to x,i+1\to x\) 表示均同意但是不合作;
-
割掉 \(S\to i,i+1\to x,i+1\to i\) 表示 \(i\) 不同意, \(i+1\) 同意。
-
割掉 \(S\to i+1,i\to x,i\to i+1\) 表示 \(i\) 同意, \(i+1\) 不同意。
-
割掉 \(x\to T\) 表示均同意并且合作。
考虑引入投资 / 喜欢的关系,如果 \(B\) 同意但是 \(A\) 没有合作,容易发现 \(S\to B,x\to T\) 的边没有被割,因此可以连接 \(B\to x\) ,流量为 \(a_i\) ;如果 \(A\) 不同意并且 \(B\) 合作,容易发现 \(S\to A,x\to T\) 的边被割,因此连接 \(x\to A\) ,流量为 \(b_i\) 。
需要注意的一点是需要从 \(x\) 向 \(i,i+1\) 建立流量为 \(\inf\) 的边,主要作用是防止一组在合作的情况下,一个人选择不同意,而建立反向边可以使外界进入的流向上回流流出。
code
#include <cstdio>
#include <algorithm>
using namespace std;
const int max1 = 5000;
int n, m;
struct Graph_Net
{
int s, t;
struct Node
{ int next, v; long long flow; } edge[max1 * 26 + 5];
int head[max1 * 3 + 5], now[max1 * 3 + 5], total;
int dis[max1 * 3 + 5], que[max1 * 3 + 5], L, R;
void Clear ()
{
s = n + n + n + 1, t = s + 1;
for ( int i = 1; i <= t; i ++ )
head[i] = 0;
total = 0;
return;
}
void Add ( int u, int v, long long flow )
{
edge[++total].v = v;
edge[total].flow = flow;
edge[total].next = head[u];
head[u] = total;
return;
}
void Add_Edge ( int u, int v, long long flow )
{ return Add(u, v, flow), Add(v, u, 0LL); }
bool Bfs ()
{
for ( int i = 1; i <= t; i ++ )
dis[i] = 0x3f3f3f3f;
dis[s] = 0; L = R = 1; que[R] = s;
while ( L <= R )
{
int x = que[L++];
now[x] = head[x];
if ( x == t )
return true;
for ( int i = head[x]; i; i = edge[i].next )
{
int v = edge[i].v; long long flow = edge[i].flow;
if ( flow && dis[v] == 0x3f3f3f3f )
{
dis[v] = dis[x] + 1;
que[++R] = v;
}
}
}
return false;
}
long long Dfs ( int x, long long sum )
{
if ( x == t )
return sum;
long long res, k; res = 0;
for ( int i = now[x]; i && sum; i = edge[i].next )
{
now[x] = i;
int v = edge[i].v; long long flow = edge[i].flow;
if ( flow && dis[v] == dis[x] + 1 )
{
k = Dfs(v, min(sum, flow));
if ( !k )
dis[v] = 0x3f3f3f3f;
else
{
edge[i].flow -= k;
if ( i & 1 )
edge[i + 1].flow += k;
else
edge[i - 1].flow += k;
res += k;
sum -= k;
}
}
}
return res;
}
long long Dinic ()
{
long long ans = 0;
while ( Bfs() )
ans += Dfs(s, 0x3f3f3f3f3f3f3f3f);
return ans;
}
}Graph;
int main ()
{
int A1, A2, B1, B2, C1, C2;
scanf("%d%d", &n, &m);
Graph.Clear();
for ( int i = 1; i <= n; i ++ )
{
scanf("%d%d%d%d%d%d", &A1, &B1, &C1, &A2, &B2, &C2);
Graph.Add_Edge(i + i - 1, n + n + i, A1);
Graph.Add_Edge(n + n + i, i + i - 1, 0x3f3f3f3f3f3f3f3f);
Graph.Add_Edge(Graph.s, i + i - 1, B1);
Graph.Add_Edge(i + i - 1, i + i, C1);
Graph.Add_Edge(i + i, n + n + i, A2);
Graph.Add_Edge(n + n + i, i + i, 0x3f3f3f3f3f3f3f3f);
Graph.Add_Edge(Graph.s, i + i, B2);
Graph.Add_Edge(i + i, i + i - 1, C2);
Graph.Add_Edge(n + n + i, Graph.t, A1 + A2);
}
for ( int i = 1; i <= m; i ++ )
{
scanf("%d%d%d%d", &A1, &A2, &B1, &B2);
C1 = ( A1 + 1 >> 1 ) + n + n;
C2 = ( A2 + 1 >> 1 ) + n + n;
Graph.Add_Edge(A2, C1, B1);
Graph.Add_Edge(C2, A1, B2);
}
printf("%lld\n", Graph.Dinic());
return 0;
}
T4 rint
概率与期望。
考虑枚举最终的最大值并求解这个最大值出现的概率,恰好的问题并不好解决,考虑求解最大值 \(\le i\) 的概率 \(f_i\) ,由于每个位置选择 \(\le i\) 的数的概率为 \(\tfrac{i}{H}\) ,选择 \(>i\) 的数的概率为 \(\tfrac{H-i}{H}\) ,考虑枚举 \(\le i\) 的数的个数,我们将 \(\le i\) 的数看做 \(0\) ,将 \(\ge i\) 的数看做 \(1\) ,这相当于求解满足每个询问区间都包含至少一个 \(0\) 的方案数。
容易发现满足嵌套关系的区间中较大的区间限制无效,去掉无效区间后发现有效区间满足右端点随左端点单调右移,考虑将所有区间按照左端点递增排序。
设 \(f_{i,j}\) 表示当前考虑了前 \(i\) 个位置,第 \(i\) 个位置一定为 \(0\) ,已经选择了 \(j\) 个 \(0\) 的方案数,设 \(maxid_i\) 表示覆盖 \(i\) 位置编号最大的区间, \(minid_i\) 表示覆盖 \(i\) 位置编号最小的区间,转移有:
\[f_{i,j}=\sum f_{k,j-1}\\ (maxid_k+1\ge minid_i) \]发现合法的 \(k\) 是一段连续的区间,因此可以用前缀和优化做到 \(O(n^2)\) 。(但是作者很懒,直接二分合法的 \(k\) ,复杂度为 \(O(n^2\log n)\))
code
#include <cstdio>
#include <algorithm>
using namespace std;
const int max1 = 2000;
const int mod = 666623333;
int n, h, q, len;
struct Question
{ int L, R; } qus[max1 + 5], tmp[max1 + 5];
int maxid[max1 + 5], minid[max1 + 5];
int f[max1 + 5][max1 + 5], sum[max1 + 5][max1 + 5], g[max1 + 5];
int power1[max1 + 5], power2[max1 + 5], P[max1 + 5], ans;
void Add ( int &x, int y )
{
x = x + y;
if ( x >= mod )
x = x - mod;
return;
}
int Quick_Power ( int base, int p )
{
int res = 1;
while ( p )
{
if ( p & 1 )
res = 1LL * res * base % mod;
p >>= 1;
base = 1LL * base * base % mod;
}
return res;
}
int main ()
{
scanf("%d%d%d", &n, &h, &q);
for ( int i = 1; i <= q; i ++ )
scanf("%d%d", &tmp[i].L, &tmp[i].R);
sort(tmp + 1, tmp + 1 + q, [&] ( const Question &A, const Question &B ) { return A.R - A.L < B.R - B.L; });
for ( int i = 1; i <= q; i ++ )
{
bool flag = false;
for ( int k = 1; k <= i - 1; k ++ )
if ( tmp[k].L >= tmp[i].L && tmp[k].R <= tmp[i].R )
flag = true;
if ( !flag )
qus[++len] = tmp[i];
}
sort(qus + 1, qus + 1 + len, [&] ( const Question &A, const Question &B ) { return A.L < B.L; });
for ( int i = 0; i <= n; i ++ )
maxid[i] = 0, minid[i] = len + 1;
maxid[0] = minid[0] = 0;
for ( int i = 1; i <= len; i ++ )
for ( int k = qus[i].L; k <= qus[i].R; k ++ )
maxid[k] = max(maxid[k], i), minid[k] = min(minid[k], i);
for ( int i = 1; i <= n; i ++ )
if ( !maxid[i] )
maxid[i] = maxid[i - 1];
for ( int i = n - 1; i >= 0; i -- )
if ( minid[i] == len + 1 )
minid[i] = minid[i + 1];
f[0][0] = sum[0][0] = 1;
for ( int k = 1; k <= n; k ++ )
{
sum[k][0] = ( sum[k - 1][0] + f[k][0] ) % mod;
for ( int j = 1; j <= n; j ++ )
{
int i = lower_bound(maxid, maxid + 1 + n, minid[k] - 1) - maxid;
if ( !i )
f[k][j] = sum[k - 1][j - 1];
else
f[k][j] = ( sum[k - 1][j - 1] - sum[i - 1][j - 1] + mod ) % mod;
sum[k][j] = ( sum[k - 1][j] + f[k][j] ) % mod;
}
}
for ( int i = 0; i <= n; i ++ )
for ( int j = 0; j <= i; j ++ )
if ( maxid[i] == len )
Add(g[j], f[i][j]);
for ( int i = 1; i <= h; i ++ )
{
power1[0] = power2[0] = 1;
for ( int j = 1; j <= n; j ++ )
{
power1[j] = 1LL * power1[j - 1] * i % mod;
power2[j] = 1LL * power2[j - 1] * ( h - i ) % mod;
}
for ( int j = 1; j <= n; j ++ )
P[i] = ( P[i] + 1LL * power1[j] * power2[n - j] % mod * g[j] % mod ) % mod;
}
for ( int i = h; i >= 1; i -- )
{
P[i] = ( P[i] - P[i - 1] + mod ) % mod;
ans = ( ans + 1LL * P[i] * i ) % mod;
}
ans = 1LL * ans * Quick_Power(Quick_Power(h, n), mod - 2) % mod;
printf("%d\n", ans);
return 0;
}