前言
题解区的方法思维难度都过大(?),提供一种极其容易的方法。
思路
题目就是求 \(\sum\limits_{i=x_1}^{x_2}\sum\limits_{j=y_1}^{y_2}a_{i,j}\)。所以很容易想到先算 \(\sum\limits_{j=y_1}^{y_2}a_{i,j}\)。
这个并不困难:
- 如果 \(i\) 是奇数,那一行应该形如 \(x, 0, x+2, 0, x+4, 0, \cdots\) 这样子的。所以等差数列求和一下 \(x+(x+2)+(x+4)+\cdots+\text{end}\) 即可。
- 如果 \(i\) 是偶数,那一行应该形如 \(0, x, 0, x+2, 0, x+4, \cdots\) 这样子的。同样的等差数列,只是首项末项改一下就行。
于是可以被实现为 \(f(i, l, r)\),具体见文末代码。答案就变成了 \(\sum\limits_{i=x_1}^{x_2}f(i,y_1,y_2)\)。
然后考虑如何快速计算。
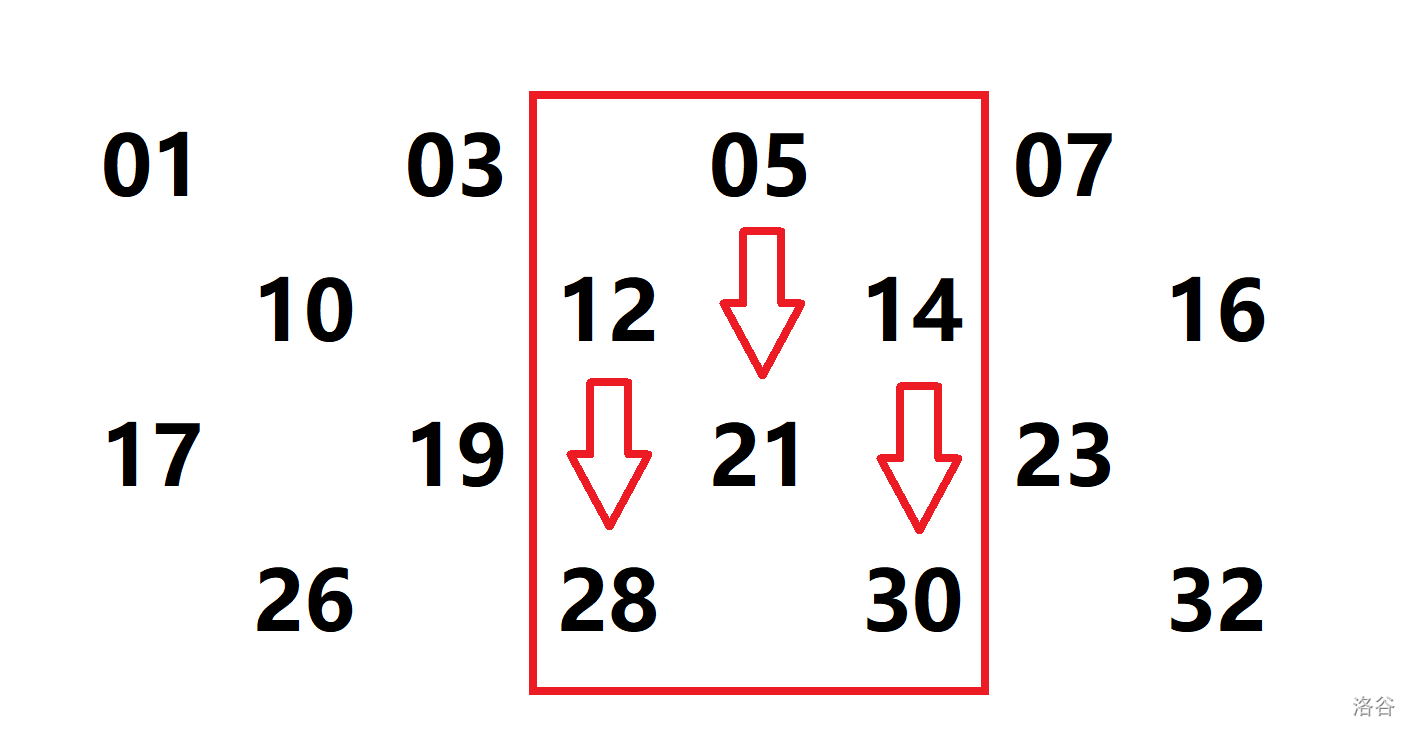
发现公差固定。所以对于 \(i\) 同奇偶的那些行来说,他们的 \(f(i)\) 也是呈等差数列的。
所以随便实现一下就做完了。代码会比别的办法的代码好理解很多。注意 \(\div 2\) 使用逆元实现。
代码
#include <iostream>
#include <cstdio>
using namespace std;
const int mod = 998244353, inv = 499122177; //inv是指除以2
int n, m;
int f(int id, int l, int r) //id行[l,r]列,总和
{
if (id & 1) //奇数列
{
int st = (l & 1) ? l : l + 1, ed = (r & 1) ? r : r - 1;
if (st > ed) return 0;
int cnt = (ed - st) / 2 + 1;
int tmp = 1ll * (id - 1) * m % mod; st = (tmp + st) % mod, ed = (tmp + ed) % mod;
return 1ll * (st + ed) * cnt % mod * inv % mod;
}
else //偶数列
{
int st = (l & 1 ^ 1) ? l : l + 1, ed = (r & 1 ^ 1) ? r : r - 1;
if (st > ed) return 0;
int cnt = (ed - st) / 2 + 1;
int tmp = 1ll * (id - 1) * m % mod; st = (tmp + st) % mod, ed = (tmp + ed) % mod;
return 1ll * (st + ed) * cnt % mod * inv % mod;
}
}
void solve()
{
int x1, y1, x2, y2, ans = 0;
scanf("%d%d%d%d", &x1, &x2, &y1, &y2);
//for (int i = x1; i <= x2; i++) ans = (ans + f(i, y1, y2)) % mod;
int st = (x1 & 1) ? x1 : x1 + 1, ed = (x2 & 1) ? x2 : x2 - 1; //奇数行
if (st <= ed)
{
int cnt = (ed - st) / 2 + 1;
ans += 1ll * (f(st, y1, y2) + f(ed, y1, y2)) * cnt % mod * inv % mod, ans %= mod;
}
st = (x1 & 1 ^ 1) ? x1 : x1 + 1, ed = (x2 & 1 ^ 1) ? x2 : x2 - 1; //偶数行
if (st <= ed)
{
int cnt = (ed - st) / 2 + 1;
ans += 1ll * (f(st, y1, y2) + f(ed, y1, y2)) * cnt % mod * inv % mod, ans %= mod;
}
printf("%d\n", ans);
}
int main()
{
int q; scanf("%d%d%d", &n, &m, &q);
while (q--) solve();
return 0;
}
希望能帮助到大家!
标签:tmp,int,题解,ABC269F,st,ed,id,mod From: https://www.cnblogs.com/liangbowen/p/17374600.html