2-SAT问题

\(2-SAT\)问题是一种在约束条件下的变量取值问题。该问题通常可以转化这样的模型：有\(n\)个变量，每一个变量只有两种取值，另有多个对这些变量的约束条件，问这些变量是否有一组取值满足所有的约束条件。

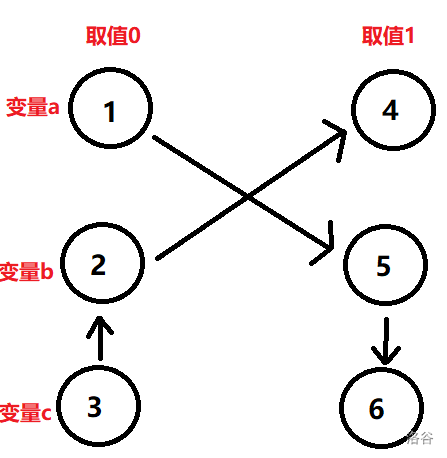
对于这类问题，我们一般的解决方案是把它抽象成一个图（如下）。这个图有\(2n\)个节点，分别是这\(n\)个变量的\(2\)种取值（视作\(0\)和\(1\)）。一般把图的 \(1\)~\(n\) 号节点分别设为 \(1\)~\(n\) 个变量的\(0\)取值， \(n+1\)~\(2n\) 号节点分别设为 \(1\)~\(n\)个变量的\(1\)取值。然后，我们用所给的约束条件来进行建边。如果变量\(a\)取值\(x\)时，变量\(b\)必须取值\(y\)。（\(x、y \in \{0,1\}\)），那么我们就连一条从\(a+x*n\)到\(b+y*n\)的有向边。把所有的边建好以后，对这个图跑一遍\(Tarjan\)，求出强连通分量。若存在一个\(\leqslant n\)的节点\(k\)与\(k+n\)在同一个强连通分量内，说明当变量取值为\(k\)的时候，他一定得取值\(k+n\)，显然矛盾，即不存在这样的一组取值使得所有约束条件被满足。反之就一定存在。

例题：[JSOI2010]满汉全席

思路：

每个厨师的两样喜好菜品可以看做一个约束条件，对于这两样菜品，如果其中一种食材已经被做成了另一样菜，那么剩下的这种食材就只能做这种菜。可以设汉式为0，满式为1，建图跑\(Tarjan\)即可。

代码：

#include<bits/stdc++.h>
#define MAXN 110
#define MAXM 1010
using namespace std;
int k,n,m,ans;
string s;
struct png
{
    int met[3],hm[3];
}p[MAXM];
struct edge
{
    int to,nxt;
}ed[MAXM<<1];
int head[MAXN<<1],tt=0;
void add(int u,int v)
{
    ed[++tt].to=v;
    ed[tt].nxt=head[u];
    head[u]=tt;
}
int dfn[MAXN<<1],low[MAXN<<1],tot=0;
stack<int>arr;
int co[MAXN<<1],col=0;
void tarjan(int st)
{
    dfn[st]=low[st]=++tot;
    arr.push(st);
    for(int i=head[st];i;i=ed[i].nxt)
    {
        int v=ed[i].to;
        if(!dfn[v])
        {
            tarjan(v);
            low[st]=min(low[st],low[v]);
        }
        else if(!co[v])low[st]=min(low[st],dfn[v]);
    }
    if(low[st]==dfn[st])
    {
        co[st]=++col;
        while(!arr.empty()&&arr.top()!=st)
        {
            co[arr.top()]=col;
            arr.pop();
        }
        arr.pop();
    }
}
int num(string ss)
{
    int ret=0;
    for(int i=1;i<ss.length();i++)
        ret=ret*10+(s[i]-'0');
    return ret;
}
int main()
{
    scanf("%d",&k);
    while(k--)
    {
        scanf("%d%d",&n,&m);
        memset(dfn,0,sizeof(dfn));
        memset(low,0,sizeof(low));
        memset(co,0,sizeof(co));
        memset(ed,0,sizeof(ed));
        memset(head,0,sizeof(head));
        tt=tot=col=0;
        while(!arr.empty())arr.pop();
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=2;j++)
            {
                cin>>s;
                if(s[0]=='h')p[i].hm[j]=0;
                else p[i].hm[j]=1;
                p[i].met[j]=num(s);
            }
            add(p[i].met[1]+(!p[i].hm[1])*n,p[i].met[2]+p[i].hm[2]*n);
            add(p[i].met[2]+(!p[i].hm[2])*n,p[i].met[1]+p[i].hm[1]*n);
        }
        for(int i=1;i<=n;i++)
            if(!dfn[i])
                tarjan(i);
        bool flag=0;
        for(int i=1;i<=n;i++)
            if(co[i]==co[i+n])flag=1;
        if(!flag)printf("GOOD\n");
        else printf("BAD\n");
    }
    return 0;
}
···