【树形DP入门题】NO337 打家劫舍III

【树形DP入门题】337. 打家劫舍 III

小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。

除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。

给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额 。

示例 1:

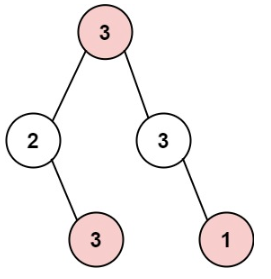
输入: root = [3,2,3,null,3,null,1]
输出: 7 
解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7

示例 2:

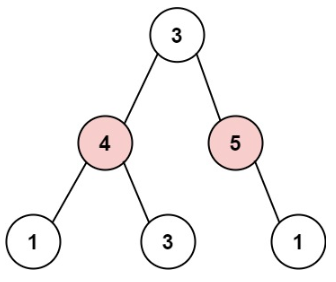
输入: root = [3,4,5,1,3,null,1]
输出: 9
解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9

提示：

• 树的节点数在 [1, 104] 范围内
• 0 <= Node.val <= 104

暴力解法

    public int rob(TreeNode root) {
        if(root == null) {
            return 0;
        }

        // 偷父节点
        var result1 = root.val;
        if(root.left != null) {
            result1 += rob(root.left.left) + rob(root.left.right);
        }

        if(root.right != null) {
            result1 += rob(root.right.left) + rob(root.right.right);
        }

        // 不偷父节点
        var result2 = 0;
        result2 += rob(root.left);
        result2 += rob(root.right);

        return Math.max(result1, result2);
    }

• 时间复杂度O(n^2)，遍历全部节点以及他们的孙子节点，不是太准确，因为涉及到孙子节点的重复计算（计算了root节点的孙子节点之后，又计算root子节点的左右孩子节点的时候，又把孙子节点计算了一次）
• 空间复杂度O(logn)

记忆化递推

HashMap<TreeNode, Integer> f = new HashMap<>();

    public int rob(TreeNode root) {
        if(root == null) {
            return 0;
        }
        if(f.get(root) != null) {
            return f.get(root);
        }

        // 偷父节点
        var result1 = root.val;
        if(root.left != null) {
            result1 += rob(root.left.left) + rob(root.left.right);
        }

        if(root.right != null) {
            result1 += rob(root.right.left) + rob(root.right.right);
        }

        // 不偷父节点
        var result2 = 0;
        result2 += rob(root.left);
        result2 += rob(root.right);

        var result = Math.max(result1, result2);
        f.put(root, result);

        return result;
    }

• 记忆化递推避免重复计算子孙节点

动态规划：状态标记的递归

​ 在上面两种方法中没有对节点 偷与不偷得到的最大金钱数 进行记录，因此每次都需要进行实时计算：每次root计算都要举例一遍子节点偷与不偷的情况，子节点再往下递归然后回溯（尽管hash避免了重复计算），而如果能够记录，则直接能够根据子节点偷与不偷的的最大值判断当前节点偷还是不偷，就免去了子节点往下的递归然后回溯的过程。

    public int rob(TreeNode root) {
        var res = robAction1(root);
        return Math.max(res[0], res[1]);
    }


    public int[] robAction1(TreeNode root) {
        var res = new int[2];
        if(root == null) {
            return res;
        }
        var left = robAction1(root.left);
        var right = robAction1(root.right);
        // 不选当前节点
        res[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
        // 选择当前节点
        res[1] = root.val + left[0] + right[0];

        return res;
    }