二叉树的创建和中序及后序遍历

二叉树的创建和中序及后序遍历

二叉的先序创建

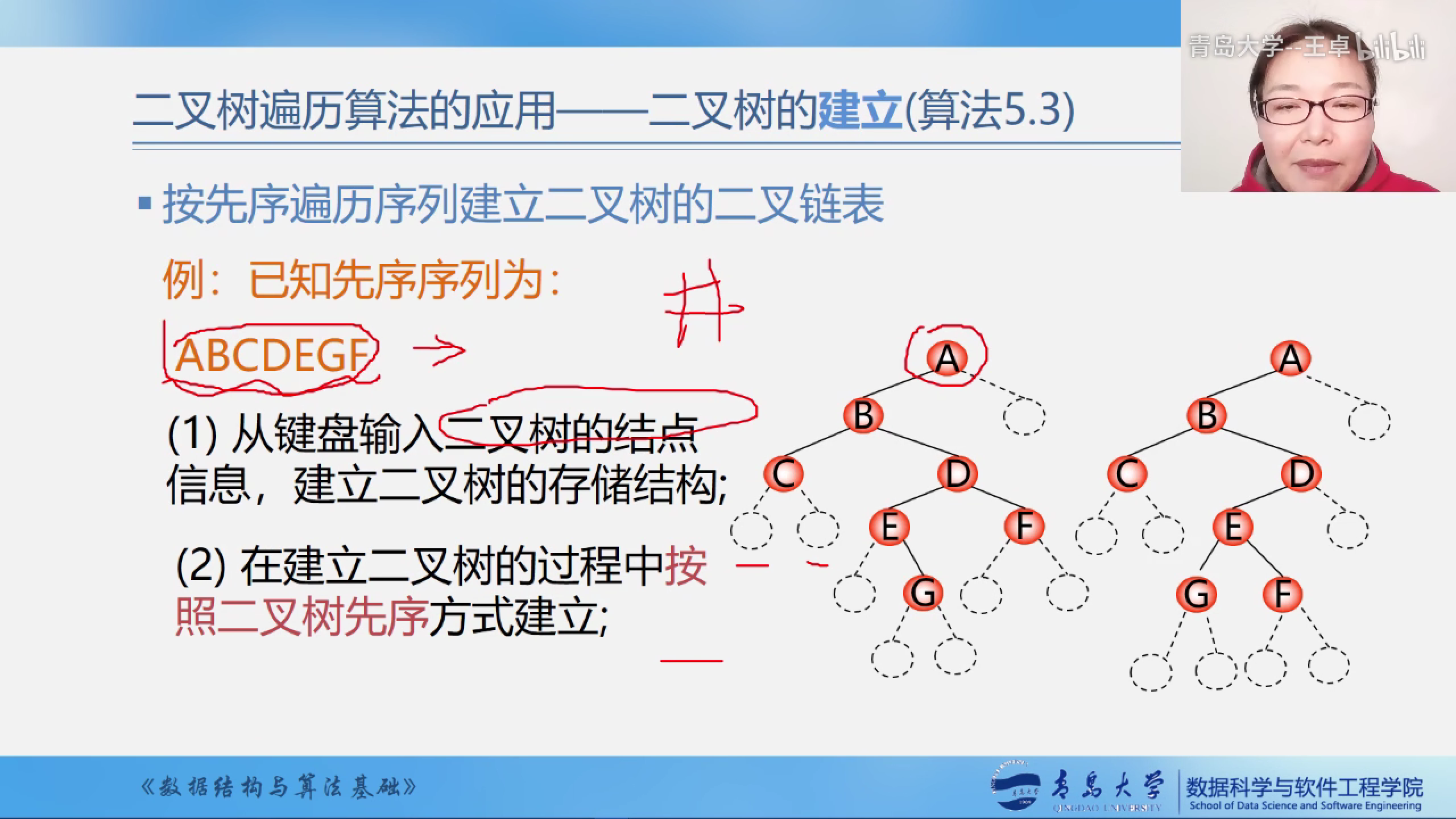
使用#号来表示该结点为null

实现代码

先进行先序创建然后进行先序遍历

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <vector>
#include <cstring>
#include <unordered_set>
#include <set>
#include <stack>
#include <map>
#include <cmath>
#include <sstream>
#include <queue>
//#define int long long
#define yes cout<<"YES"<<'\n'
#define no 	cout<<"NO"<<'\n'

using namespace std;

typedef struct BiNode {
	char data;//数据域
	struct BiNode *lchild;//左孩子指针
	struct BiNode *rchild;//右孩子指针
} BiNode, *BiTree;//定义二叉树结点

/*
  按照先序创建
 */
void CreateBiTree(BiTree &T) {
	char ch;
	cin >> ch;
	if (ch == '#') {
		T = NULL;
		return;
	} else {
		T = new BiNode;//开辟结点
		T->data = ch; //对数据域赋值
		CreateBiTree(T->lchild);//建立左子树
		CreateBiTree(T->rchild);//建立右子树
	}
}
/*
  前序遍历
 */
void DLR(BiTree T) {
	if (T == NULL) {
		return ;
	} else {
		char ch = T->data;
		cout << ch;
		DLR(T->lchild);
		DLR(T->rchild);
	}

}
/*
  中序遍历
 */
void LDR(BiTree T) {
	if (T == NULL) {
		return ;
	} else {
		char ch = T->data;

		LDR(T->lchild);//先访问左子树
		cout << ch;//再访问根结点
		LDR(T->rchild);//再访问右子树
	}

}
/*
  后序遍历
 */
void LRD(BiTree T) {
	if (T == NULL) {
		return ;
	} else {
		char ch = T->data;

		LRD(T->lchild);//先访问左子树
		LRD(T->rchild);//再访问右子树
		cout << ch;//再访问根结点
	}

}

int main () {
	BiTree root = NULL;
	CreateBiTree(root);
	DLR(root);
	cout << '\n';

//	LDR(root);
//	cout<<'\n';

//	LRD(root);
	return 0;
}
/*
  abc##de#g##f###

 */

二叉树的中序遍历

1.先访问左子树

2.再访问根结点

3.最后访问右子树

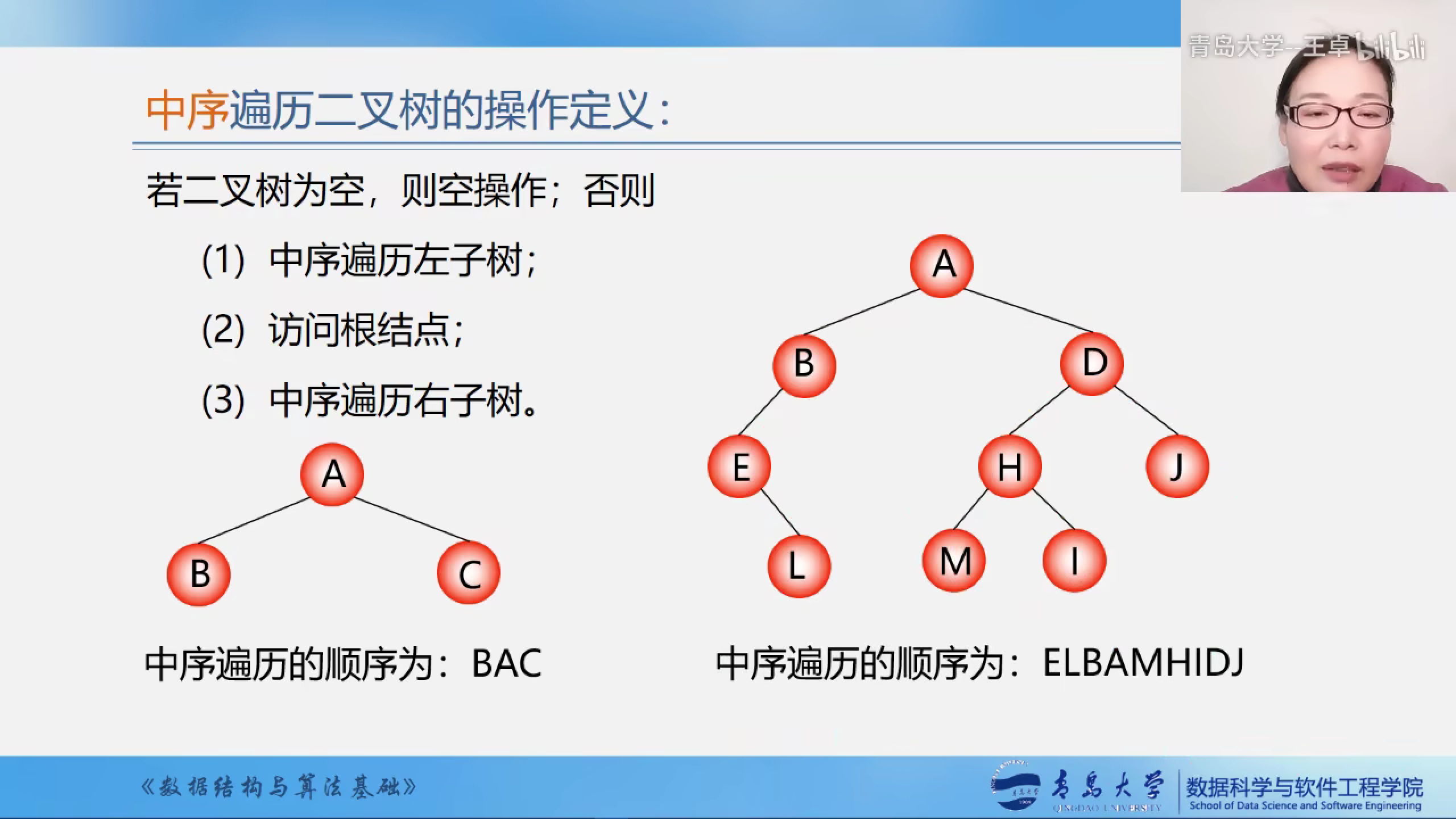
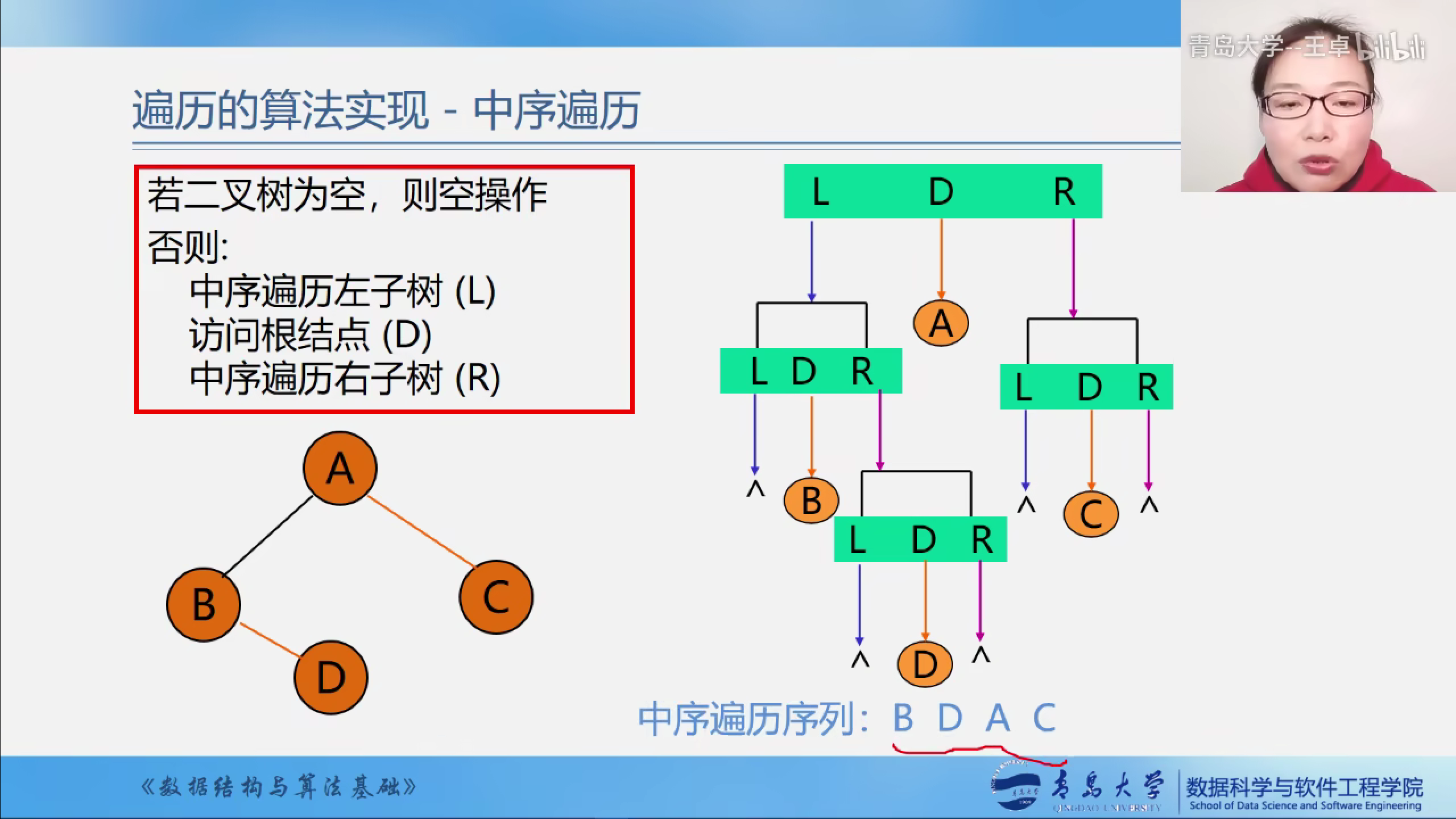
中序遍历示意图

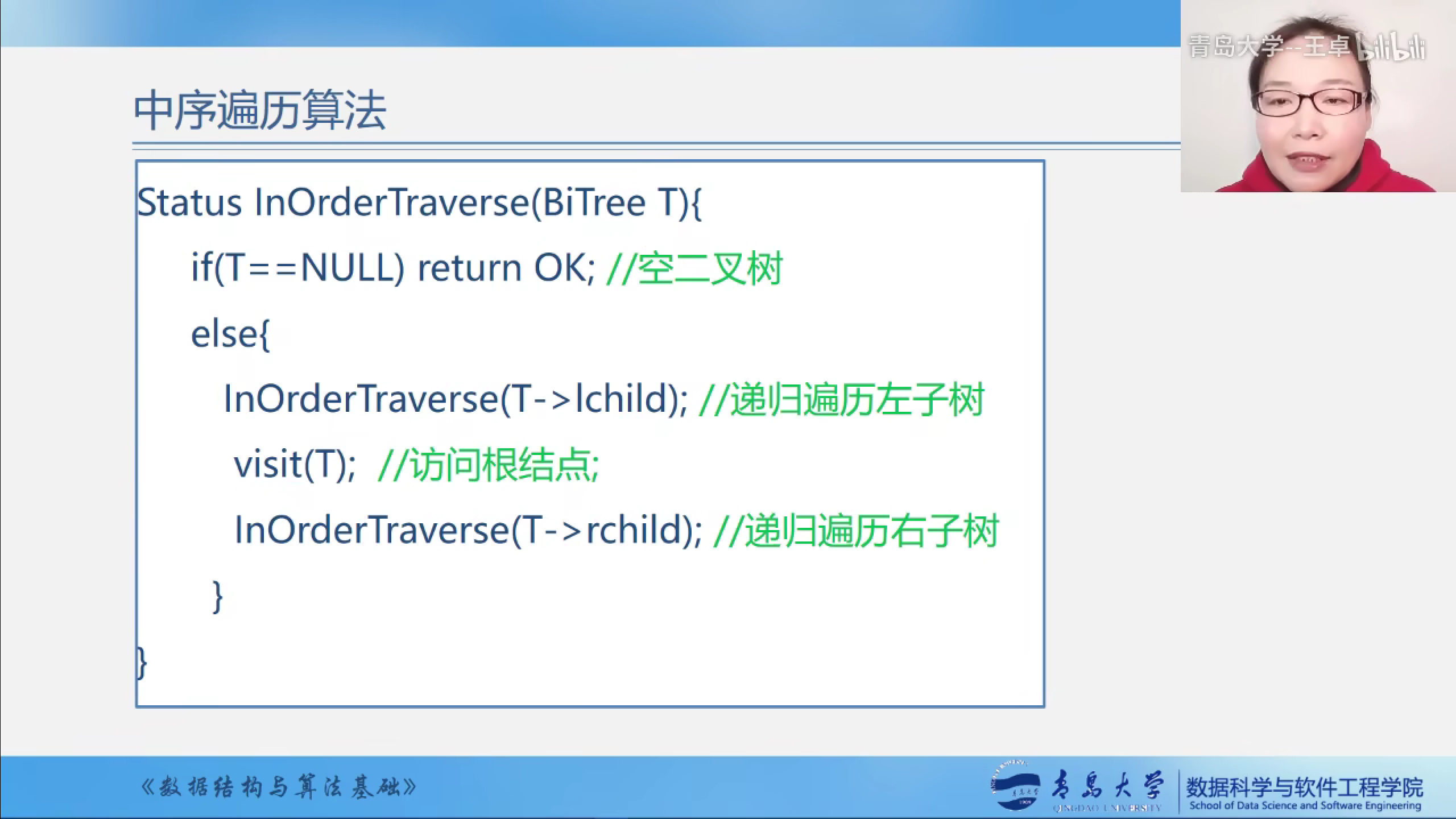
中序遍历算法实现

二叉树的后序遍历

1. 先访问左子树

2. 再访问右子树

3. 最后访根结点

   

   后序遍历的示意图

   

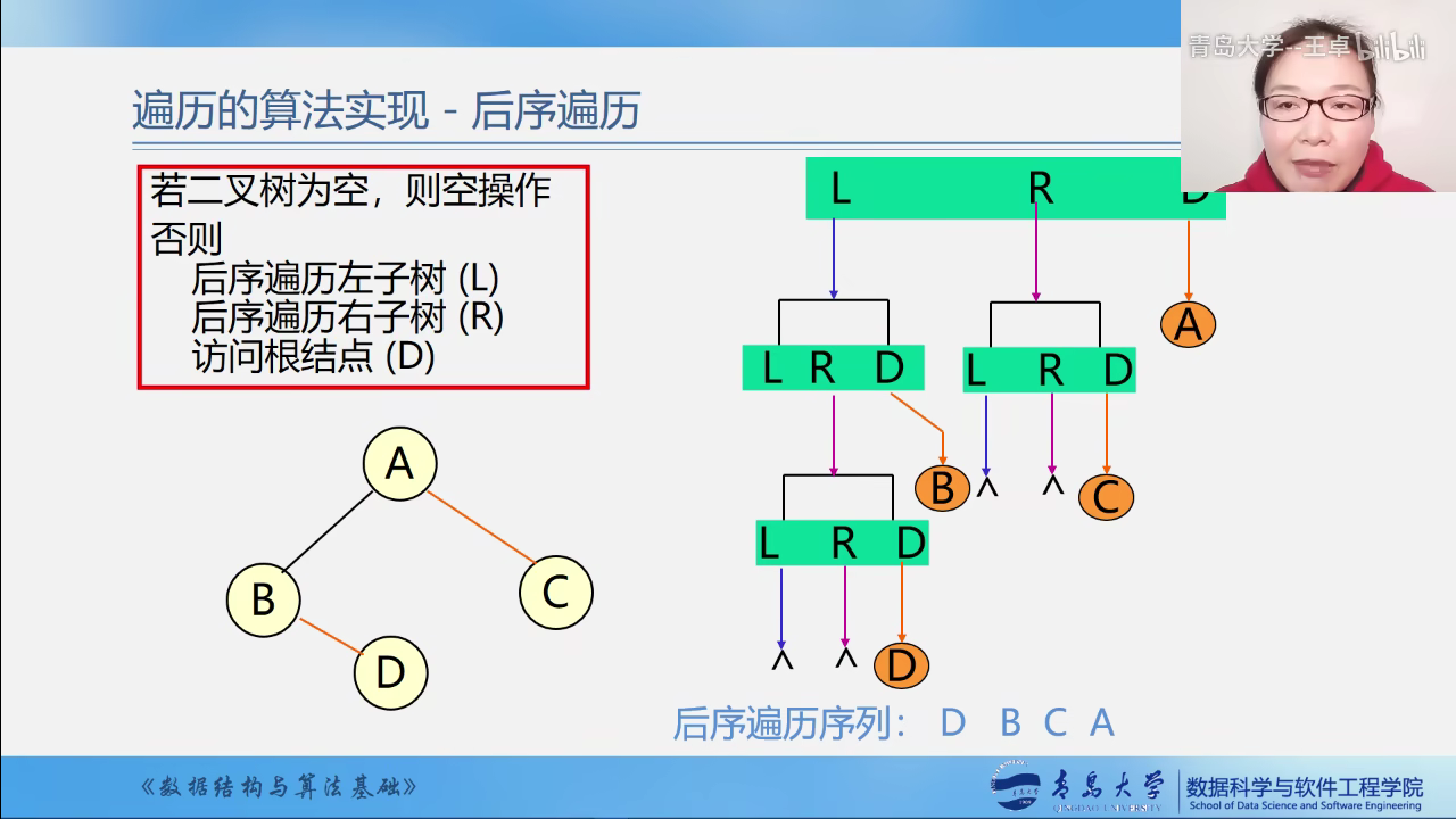
   后序遍历的算法实现

   

一道例题

第二道例题

完整的代码实现

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <vector>
#include <cstring>
#include <unordered_set>
#include <set>
#include <stack>
#include <map>
#include <cmath>
#include <sstream>
#include <queue>
#define int long long


using namespace std;

typedef struct BiNode {
	struct BiNode *lchild, *rchild;//左孩子右孩子
	char data;//数据域

} BiNode, *BiTree;

/*
  二叉树的先序创建
 */
void CreateBitree(BiTree &T) {
	char ch;
	cin >> ch;
	if (ch == ',') {
		T = NULL; //,表示该结点为空
	} else {
		T = new BiNode; //创建一个新结点
		T->data = ch; //给数据域赋值
		CreateBitree(T->lchild);//建立左子树
		CreateBitree(T->rchild);//建立右子树
	}

}
/*
  二叉树的先序遍历
 */
void DLR(BiTree T) {
	if (T == NULL) {
		return;
	} else {
		cout << T->data; //先访问根
		DLR(T->lchild);//访问左子树
		DLR(T->rchild);//访问右子树
	}



}
/*
  二叉树的中序遍历
 */
void LDR(BiTree T) {
	if (T == NULL) {
		return;
	} else {

		LDR(T->lchild);//访问左子树
		cout << T->data; //访问根
		LDR(T->rchild);//访问右子树
	}



}
/*
  二叉树的后序遍历
 */
void LRD(BiTree T) {
	if (T == NULL) {
		return;
	} else {

		LRD(T->lchild);//访问左子树
		LRD(T->rchild);//访问右子树
		cout << T->data; //访问根
	}



}

signed main () {
	BiTree root = NULL; //创建根结点
	cout << "请输入需要建立的二叉树的数值\n";
	CreateBitree(root);//创建二叉树
	cout << "下面是二叉树先序遍历结果\n";
	DLR(root);
	cout << "\n下面是二叉树中序遍历结果\n";
	LDR(root);
	cout << "\n下面是二叉树后序遍历结果\n";
	LRD(root);

	return 0;
}
/*
  abc,,de,g,,f,,,
  中序:
  cbegdfa
  后序:
  cgefdba

 */