Codeforces Round #818 (Div. 2) - D. Madoka and The Corruption Scheme

思维+组合数学

Problem - D - Codeforces

题意

有 \(2^n\) 个人进行锦标赛，编号1~\(2^n\)，每一场输的人失去比赛资格，赢的人继续。Madoka可以选择他们进行的顺序，以及决定哪一边赢得比赛。你的目标是尽量让编号小的赢得最终比赛。 主办方可以改变其中至多k场比赛的结果，即本来是左边赢的改为右边赢，本来是右边赢的改为左边。如下图所示，左边红线是你选择的胜方。而主办方改动左边的一个结果，使得最终赢的人变成3。

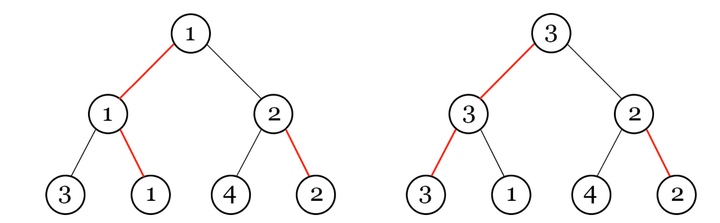
问题是，求最小的编号，使得存在一个最优方案，使得无论主办方怎么改，都可以让他赢。主办方目标是让赢的人编号更大。

思路

1. 转换为图论问题：设 Madoka 一开始规定的红边权值是 0，黑边权值是 1，记 \(f[x]\) 为从根节点到编号 x 的结点的路径边权和
2. 若主办方想让编号为 x 的成为冠军，则 \(f[x]<=k\) (主办方必须把这 \(f[x]\) 条边全部逆转)
3. 因为有 \(2^n\) 个叶子，就有 \(2^n\) 种互不相同的路径，权值为 i 的叶子相当于长度为 n 的路径上选 i 个黑边，有 \(\binom ni\) 个，所以主办方只能把 \(\sum\limits_{i=0}^{k}\binom ni\) 个叶子放到冠军，因此 Madoka 贪心地把编号最小的放到这些叶子的位置即可

代码

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>

using namespace std;
#define endl "\n"

typedef long long ll;
typedef pair<int, int> PII;

const int N = 1e5 + 10, mod = 1e9 + 7;
int n, k;
ll fac[N], finv[N];
ll qmi(ll a, ll b)
{
	ll ans = 1;
	while(b)
	{
		if (b & 1)
			ans = ans * a % mod;
		b >>= 1;
		a = a * a % mod;
	}
	return ans;
}

void presolve(int n)
{
	fac[0] = finv[0] = 1;
	for (int i = 1; i <= n; i++)
		fac[i] = fac[i-1] * i % mod;
	finv[n] = qmi(fac[n], mod - 2);
	for (int i = n - 1; i >= 1; i--)
		finv[i] = finv[i+1] * (i + 1) % mod;
}

ll C(int n, int m)
{
	if (m < 0 || n - m < 0)
		return 0;
	return fac[n] * finv[m] % mod * finv[n-m] % mod;
}
ll solve()
{
	if (k >= n)
		return qmi(2, n);
	ll ans = 0;
	for (int i = 0; i <= k; i++)
		ans = (ans + C(n, i)) % mod;
	return ans;
}
int main()
{
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin >> n >> k;
	presolve(n);
	cout << solve() << endl;
    return 0;
}