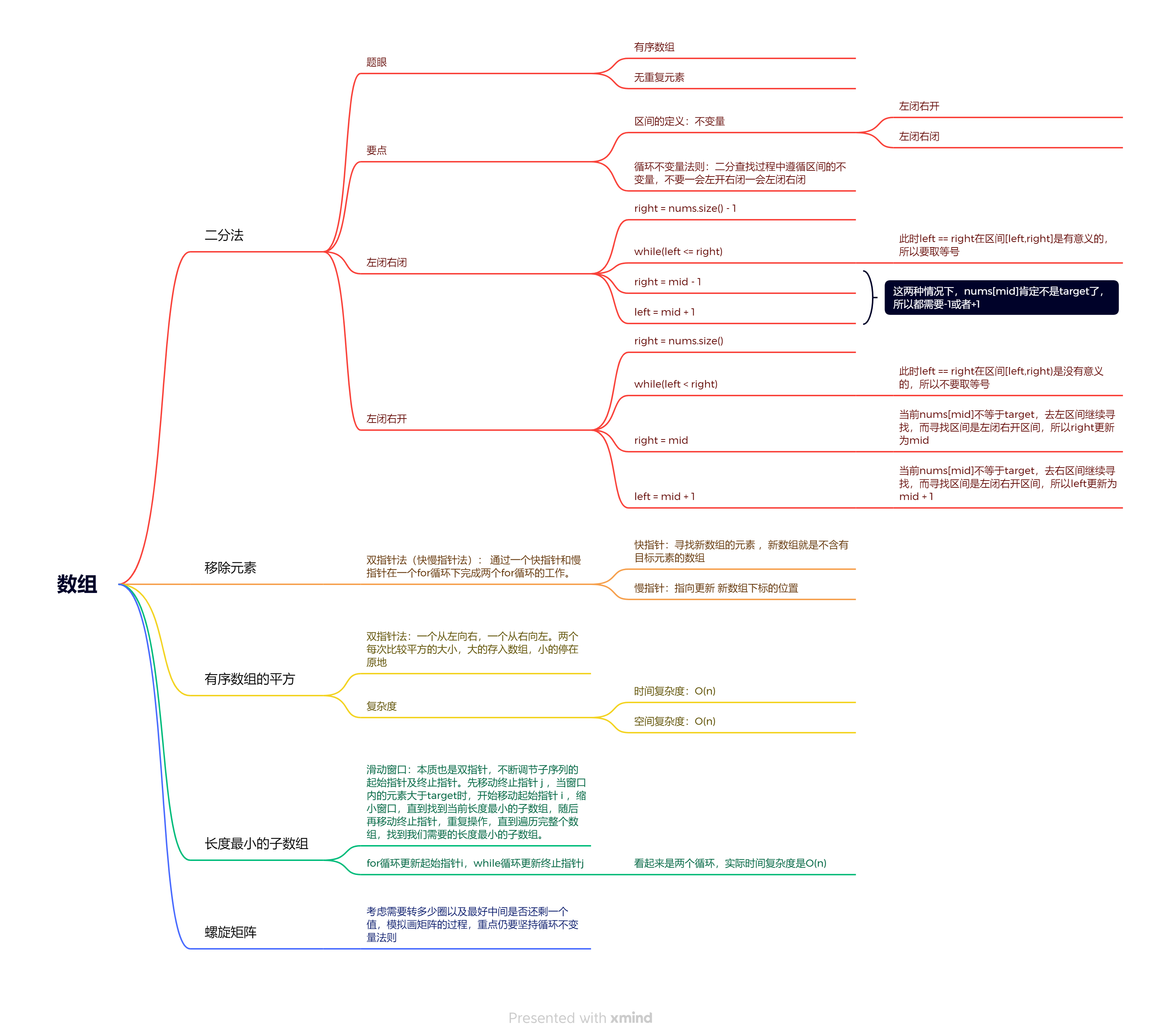
二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
- 你可以假设 nums 中的所有元素是不重复的。
- n 将在 [1, 10000]之间。
- nums 的每个元素都将在 [-9999, 9999]之间。
思路
题眼:
- 有序数组
- 无重复元素
核心:循环不变量法则
代码
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1; // [left,right]
while(left <= right)
{
int mid = left + ((right - left) / 2); // 防止left + right溢出
if(nums[mid] > target)
{
// 往左找
right = mid - 1; // nums[mid]已经不可能了,保持循环不变量原则
}
else if(nums[mid] < target)
{
// 往右找
left = mid + 1;
}
else
{
// 找到了
return mid;
}
}// end of while
return -1; // 找不到
}
};
复杂度
- 时间复杂度:O(log n)
- 空间复杂度:O(1)
移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并原地修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1: 给定 nums = [3,2,2,3], val = 3, 函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。 你不需要考虑数组中超出新长度后面的元素。
示例 2: 给定 nums = [0,1,2,2,3,0,4,2], val = 2, 函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。
你不需要考虑数组中超出新长度后面的元素。
思路
双指针法(快慢指针法): 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
定义快慢指针
- 快指针:寻找新数组的元素 ,新数组就是不含有目标元素的数组
- 慢指针:指向更新 新数组下标的位置
代码
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int slowIndex = 0;
for(int fastIndex = 0;fastIndex < nums.size();fastIndex++)
{
if(val != nums[fastIndex])
{
nums[slowIndex++] = nums[fastIndex];
}
}
return slowIndex; // 注意此处直接返回慢指针的下标
}
};
复杂度
- 时间复杂度:O(n)
- 空间复杂度:O(1)
有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1: 输入:nums = [-4,-1,0,3,10] 输出:[0,1,9,16,100] 解释:平方后,数组变为 [16,1,0,9,100],排序后,数组变为 [0,1,9,16,100]
示例 2: 输入:nums = [-7,-3,2,3,11] 输出:[4,9,9,49,121]
思路
双指针法:
数组其实是有序的, 只不过负数平方之后可能成为最大数了。
那么数组平方的最大值就在数组的两端,不是最左边就是最右边,不可能是中间。
此时可以考虑双指针法了,i指向起始位置,j指向终止位置。
定义一个新数组result,和A数组一样的大小,让k指向result数组终止位置。
如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]; 。
如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]; 。
代码
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
int k = nums.size() - 1; // k是下标,故-1
vector<int> result(nums.size(),0);
for(int i = 0,j = nums.size() - 1;i <= j;)
{
if(nums[i] * nums[i] < nums[j] * nums[j])
{
result[k--] = nums[j] * nums[j];
j--;
}
else
{
result[k--] = nums[i] * nums[i];
i++;
}
}
return result;
}
};
复杂度
- 时间复杂度:O(n)
长度最小的子数组
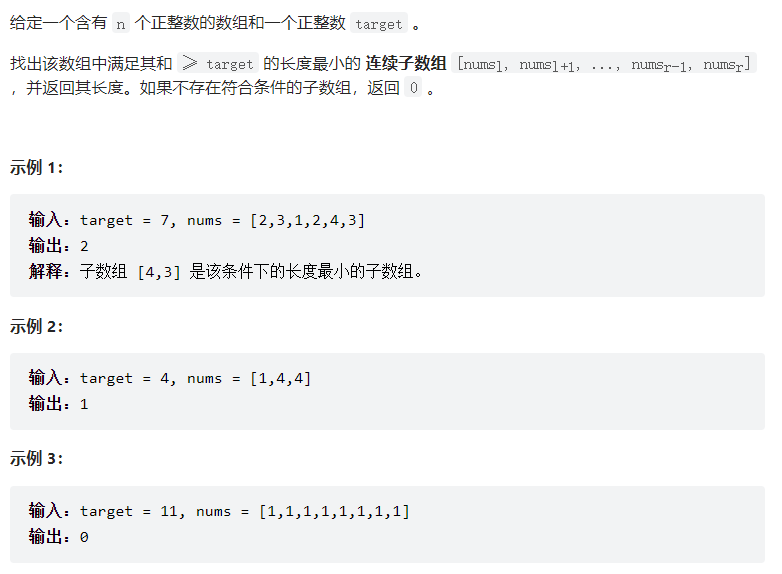
思路
暴力解法:一个for循环滑动窗口的起始位置,一个for循环为滑动窗口的终止位置,用两个for循环 完成了一个不断搜索区间的过程。
滑动窗口:不断的调节子序列的起始位置和终止位置,通过一个for循环得出我们要想的结果,降低暴力解法的时间复杂度。
使用滑动窗口主要注意三点:
-
窗口内是什么?
窗口内就是满足其和 ≥ target 的长度最小的连续子数组。
-
如何移动窗口的起始位置?
当窗口的值大于 target 时,移动起始指针,缩小窗口,找到当前最小的连续子数组
-
如何移动窗口的结束位置?
窗口的结束位置就是遍历数组的指针,也就是for循环里的索引。
代码
int minSubArrayLen(int target, int* nums, int numsSize){
int i,j,sum,result,length;
result = INT_MAX;
sum = 0; // 滑动窗口数值之和
i = 0; // 滑动窗口起始位置
length = 0; // 滑动窗口的长度
for(j = 0;j < numsSize;j++)
{
sum+=nums[j];
// 注意这里使用while,每次更新 i(起始位置),并不断比较子序列是否符合条件
while(sum > target||sum == target)
{
length = j - i +1;
result = result>length?length:result;
sum-=nums[i++];// 这里体现出滑动窗口的精髓之处,不断变更i(子序列的起始位置)
}
}
result = result==INT_MAX?0:result;
return result;
}
// 11行到16行是滑动窗口的精髓所在
复杂度
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
螺旋矩阵
给你一个正整数 n ,生成一个包含 1到 n^2 所有元素,且元素按顺时针顺序螺旋排列的 n*n 正方形矩阵 matrix 。
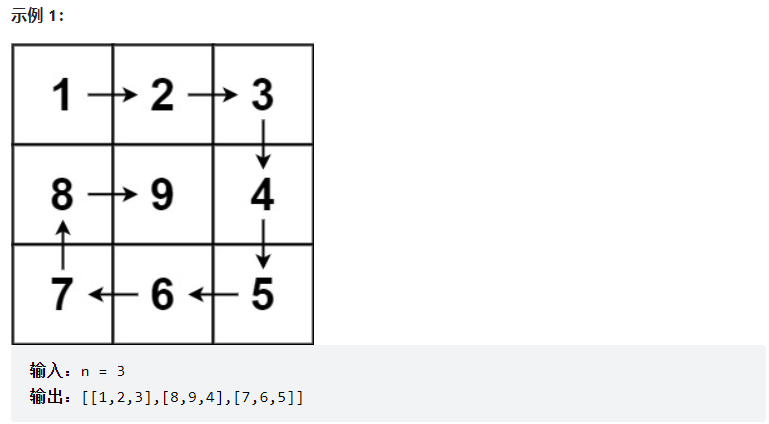
思路
关键还是要遵守循环不变量法则,模拟画矩阵的过程。必须在一开始就定好循环的规则(比如:左闭右开),后面都按照这个规则进行模拟。在写代码时,要思考在进行模拟时,让那些变量来代表那些含义(比如:循环圈数loop、起始位置startx,starty等)。
代码
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> res(n, vector<int>(n, 0));
int loop = n / 2;// 总共循环的次数(画圈的次数)
int startx = 0,starty = 0;// 定义每循环一个圈的起始位置
int count = 1;// 用来给每个格子赋值
int offset = 1;// 用来控制一圈里面每条边的长度
int i,j;
while(loop--)
{
// 以左闭右开的方式画圈
i = startx,j = starty;
// 模拟画圈的过程
// 模拟填充上行,从左到右
for(j = starty; j < n - offset; ++j)
{
res[startx][j] = count++;
}
// 模拟填充右列,从上到下
for(i = startx; i < n - offset; ++i)
{
res[i][j] = count++;
}
// 模拟填充下行,从右到左
for(;j > starty; --j)
{
res[i][j] = count++;
}
// 模拟填充左列,从下到上
for(;i > startx; --i)
{
res[i][j] = count++;
}
// 画完一圈,起始位置各自加1
startx++;
starty++;
// offset控制每一圈里每一条遍历的长度
offset++;
}
// 如果n为奇数的话,需要单独给矩阵最中间的位置赋值
if(n % 2)
{
int mid = n / 2;
res[mid][mid] = count;
}
return res;
}
};
复杂度
- 时间复杂度 O(n^2): 模拟遍历二维矩阵的时间
- 空间复杂度 O(1)
总结
二分法
一般用于查找一个有序数组中的某个值的位置或者给定的特定值的插入位置。相比把整个数组遍历一次的O(n)复杂度,二分查找可以把复杂度降低到O(logn);
何时使用
二分法一定是建立在元素有序的前提下的(或数据具有二段性),所以看到题目中出现有序数组等词时,并且要求我们查找某个值或者给一个值求插入位置,或者判断其中是否存在某个值或者利用二分思路求最大最小值等,这些都可以使用二分法。再就是要注意此时要求数据无重复。
思路及细节
二分法的思路很简单,无非就是每次根据中值判断,然后缩减区间到原来的一半;二分法最容易出错的地方在于边界和细节处理,大体逻辑并不难写出。而要处理好细节就要牢记循环不变量法则,从开始就定好一个规则(比如,左闭右闭[left,right]),然后后面都要按照这个规则来写代码,这样才不会出错。
双指针(快慢指针)法
通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
- 暴力解法时间复杂度:O(n^2)
- 双指针时间复杂度:O(n)
双指针在数组以及链表的操作中都很常见,也很灵活,需要多做题多体会。
滑动窗口
主要要理解滑动窗口如何移动 窗口起始位置,达到动态更新窗口大小的,从而得出长度最小的符合条件的长度。
滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)。
其本质其实也是双指针法
模拟行为
这种题目其实不涉及算法,只是单纯的模拟。比较重视对代码的掌控能力,做题时明确思路,不能含糊不清。这种情况一定要让思路清晰明了,遵循某个原则去写,才不容易出错。