给定一棵树,树中包含 nn 个结点(编号11~nn)和 n−1n−1 条无向边,每条边都有一个权值。
请你在树中找到一个点,使得该点到树中其他结点的最远距离最近。
输入格式
第一行包含整数 nn。
接下来 n−1n−1 行,每行包含三个整数 ai,bi,ciai,bi,ci,表示点 aiai 和 bibi 之间存在一条权值为 cici 的边。
输出格式
输出一个整数,表示所求点到树中其他结点的最远距离。
数据范围
1≤n≤100001≤n≤10000,
1≤ai,bi≤n1≤ai,bi≤n,
1≤ci≤1051≤ci≤105输入样例:
5 2 1 1 3 2 1 4 3 1 5 1 1输出样例:
2
难度:简单 时/空限制:1s / 64MB 总通过数:8103 总尝试数:12486 来源:模板题 算法标签
核心思路:(换根dp)
其实我们看到这个题目的一个想法是可以单独求出来一个节点的最长直径然后对于每一个节点取一个max就好了。以某一个节点作为根的最长路径一定是以他为根的向下的最长路径和向上的最长路径。然后我们发现一个节点的向上的最长路径是和它父节点的向下的最长路径和次长路径决定的。
先看图:
.png)
比如我们要求3的最长向上路径发现其实就是父节点2的一个次长向下路径+w[i],至于为什么不是最长下面有解析,当然图也看得很清楚了。因为会有边重复。
首先看到最大值最小不要立马想二分。这个题目我们可以转换为先求每个节点的一个最长路径,然后再是枚举每一个节点取min就好了。
我们看到求每个节点的最长路径回想到上面那题,但是那题的代码是会超时的。所以这个题目其实是对上一个题目的代码做点优化。
首先可以想怎么对当前节点进行优化呢,假如当前节点是u,当前节点的父节点是father。我们首先思考这个父节点可以对子节点做出一个什么贡献。首先我们当前子节点到父节点的距离确定了也就是w[i].所以我们只需要确定父节点的最长路劲是多少。
父节点的最长路径可以分为两类:
- 向上的最长路径,这个很好求我们上一题就知道怎么求了,先求根节点到father的最长路径再就是次长路径,然后相加就好了。所以求向上的一个路径也可以转换为求向下的一个路径的问题。
- 向下的最长路径,这里我们就需要分类讨论了。
- father节点的最长向下路径经过u,那么我们就只能在u的最长向上路径和次长向下路径取max
- father节点的最长向下路径不经过u,那么我们就可以在u的最长向下路径和最长向上路径中取max
因为我们是简单路径好马不吃回头草
下面看个图吧:
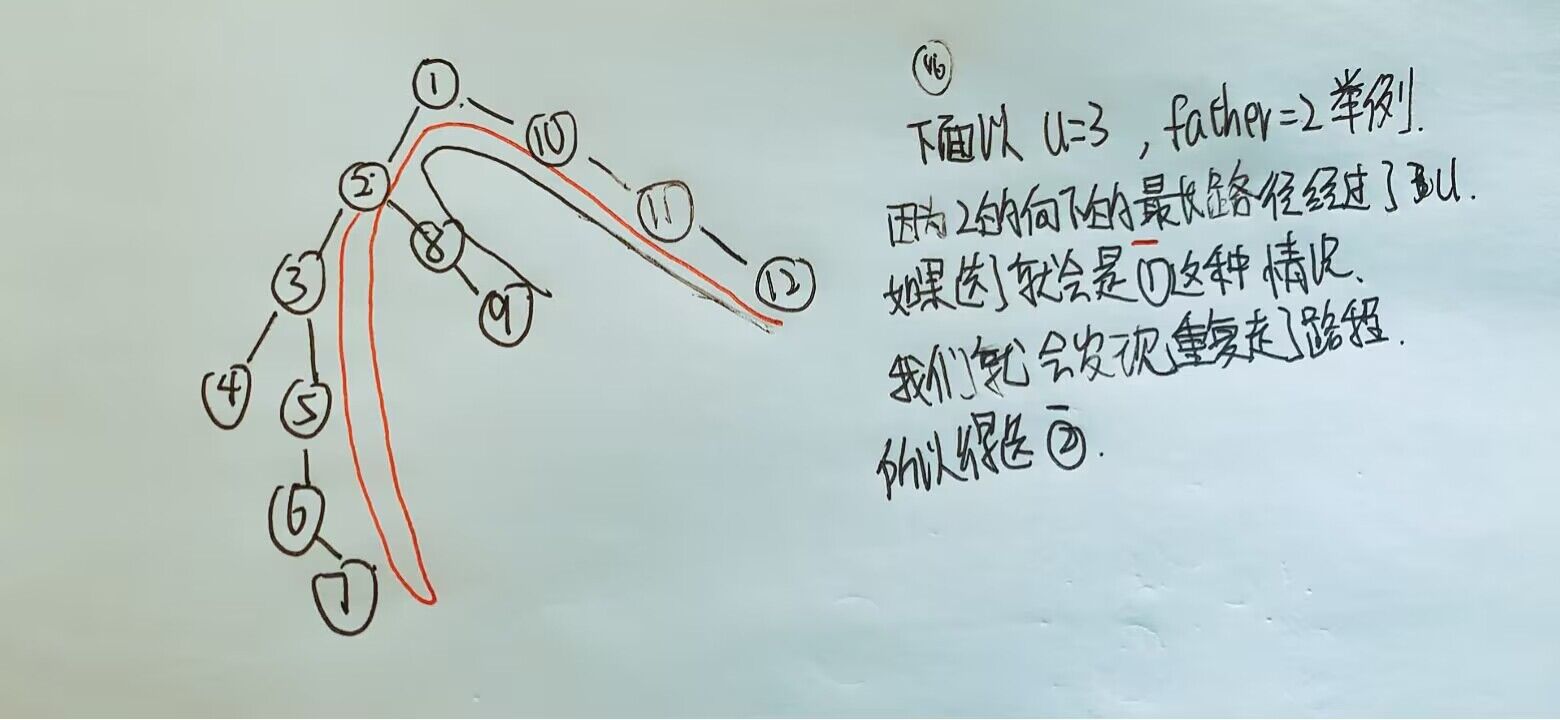
ok,解释清楚了直接上代码。
#include<iostream>
#include<cstring>
/*
d1[u]:存下u节点向下走的最长路径的长度;
d2[u]:存下u节点向下走的次长路径
p1[u]:存下的是u节点向下走的最长路径是从哪个节点下去的。也就是存的是u节点向下走的最长路径的长子
p2[u]:存下的是u节点向下走的次长路径是从哪一个节点下去的。存的是次长路径的长子。
up[u]:村下的是u节点向上走的最长路径的长度。
*/
using namespace std;
const int N=2e5+10,INF=1e9;
int d1[N],d2[N],up[N], p1[N], p2[N];
int h[N],ne[2*N],e[2*N];
int idx;
int w[N];
int n;
void add(int a,int b,int c)
{
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
}
int dfs_down(int u,int father)//返回u的最长向下路径
{
d1[u]=d2[u]=-INF;//dp初始化
for(int i=h[u];~i;i=ne[i])
{
int j=e[i];
if(j==father)
continue;
int dist=dfs_down(j,u)+w[i];
if(dist>d1[u])
{
d2[u]=d1[u];
d1[u]=dist;
p2[u]=p1[u];
p1[u]=j;
}
else if(dist>d2[u])
{
d2[u]=dist;
p2[u]=j;
}
}
if(d1[u]==-INF)//表示的是叶子节点.
d1[u]=d2[u]=0;
return d1[u];//因为我们返回的就是最长的向下的路径。
}
void dfs_up(int u,int father)//使用父节点更新子节点向上的最长路径
{
for(int i=h[u];~i;i=ne[i])
{
int j=e[i];
if(j==father)//老样子不可以有回边,要不然会陷入死循环.
continue;
if(p1[u]==j)
up[j]=max(up[u],d2[u])+w[i];
else
up[j]=max(up[u],d1[u])+w[i];
dfs_up(j,u);//因为我们采用的是从上往下所以不需要写一个回溯的做法了,也就是可以把操作放在dfs的上面。
}
}
int main()
{
cin>>n;
memset(h,-1,sizeof h);
for(int i=0;i<n-1;i++)
{
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
add(b,a,c);
}
dfs_down(1,-1);
dfs_up(1,-1);
int res=INF;
for(int i=1;i<=n;i++)
res=min(res,max(d1[i],up[i]));
cout<<res<<endl;
return 0;
}