KMP

题目描述

给定一个字符串 \(S\)，以及一个模式串 \(P\)，所有字符串中只包含大小写英文字母以及阿拉伯数字。

模式串 \(P\) 在字符串 \(S\) 中多次作为子串出现。

求出模式串 \(P\) 在字符串 \(S\) 中所有出现的位置的起始下标。

输入第一行输入整数 \(N\)，表示字符串 \(P\) 的长度。

第二行输入字符串 \(P\)。

第三行输入整数 \(M\)，表示字符串 \(S\) 的长度。

第四行输入字符串 \(S\)。

输出所有出现位置的起始下标，整数之间用空格隔开。

样例输入输出

4
aaab
8
aaacaaab

5

规定

我们规定 \(p\) 为模式串且长度为 \(n\)， \(s\) 为被查找串且长度为 \(m\)。

朴素做法

朴素做法即暴力做法，每一次都需要从头匹配到尾。

void solve(){
	for(int i=1; i<=m-n+1; i++){
		bool flag = true;
		for(int j=1; j<=n; j++){
			if(p[j] != s[i+j-1]){
				flag = false;
				break;
			}
		}
		if(flag){
			cout << i << ' ';
		}
	}
}

KMP

KMP，即 Knuth-Morris-Pratt 算法。

在朴素做法中，如果前面的部分 \(p\) 与 \(s\) 都相同，但突然在某一位置上产生差异， 那么 \(p\) 将从头开始重新匹配，降低效率。

在 KMP 算法中，如果匹配失败，\(p\) 将不会退到开头，而是找到一个位置，使得这个位置可以继续往后匹配。这个位置就是 \(nxt_i\) 的值。

\(nxt_i\) 的含义及求解

\(nxt_i\) 表示的是在 \(p\) 的前 \(i\) 个字符中，前 \(nxt_i\) 个字符与后 \(nxt_i\) 个字符相等，并取得所有满足情况的 \(nxt_i\) 的最大值。也可以称之为最大公共前后缀。

例如，若 \(p = \texttt{"aaacaaab"}\)，那么

\(nxt_1 = 1, nxt_2 = 2, nxt_3 = 3, nxt_4 = 0, nxt_5 = 1, nxt_6 = 2, nxt_7 = 3, nxt_8 = 0\)。

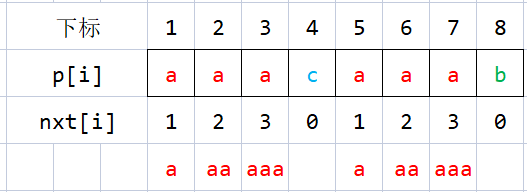
如何求出 \(nxt_i\) 的值呢？

假设下图为 \(p\) 模式串：

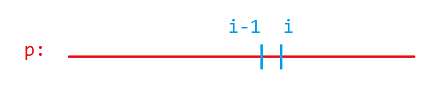
现在要将这个字符串往右移，原来 \(i-1\) 的位置要移动到 \(j\) 的位置。

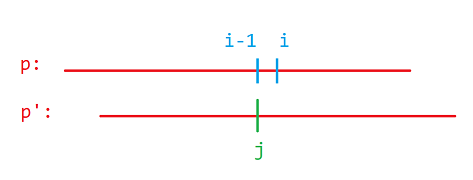
现在已知：\(i-1\) 能匹配到 \(j\)，问 \(i\) 能不能匹配到 \(j+1\) 的位置。

如果 \(p_i \ne p_{j+1}\)，那么它将继续向后匹配，此时要将 \(j\) 重新移动到 \(nxt_j\) 的位置。

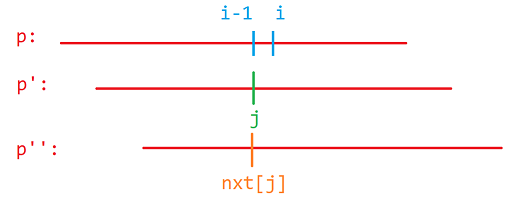
如果仍然不匹配，那么将 \(j\) 再次移动，递归执行，直到匹配成功或 \(j=0\) 时结束。

如果在某一次匹配成功了，那么记录下 \(nxt_i = j\)，并让 \(j\) 向后移动。

以上操作循环执行。

void init_nxt(){
    for(int i=2, j=0; i<=n; i++){
        while(j && p[i] != p[j + 1]){
            j = nxt[j];
        }

        if(p[i] == p[j + 1]){
            j++;
        }

        nxt[i] = j;
    }
}

KMP 匹配

求完 \(nxt_i\) 后，就要开始匹配了。

下图中蓝线为 \(s\)，红线为 \(p\)。

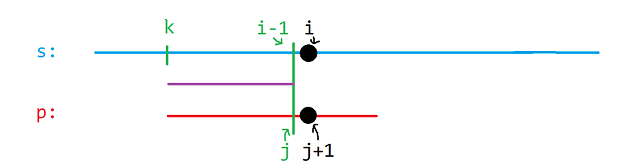
现在已知，图中从 \(k\) 到 \(i-1\) 都已经匹配成功，及紫线部分两串相同，但是 \(s_i \ne p_{j+1}\)，此时就需要重新匹配。

如果使用朴素算法，这是需要从把 \(j\) 归为 \(1\) 重新匹配。但在 KMP 算法中，我们已经提前处理好了 \(nxt_j\)，因此这里可以直接跳过多余的步骤。

具体地，对于上图，我们已经求解出了 \(nxt_j\) 的值。

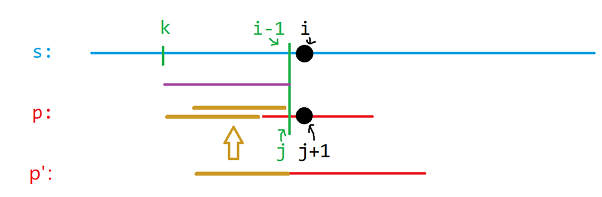
图中共有三处褐色线段。不难分析出，这三段的内容都是相同的，而这条褐色的线恰好是 \(nxt_j\) 的含义，因此如果匹配失败就可以直接将 \(j\) 赋值为 \(nxt_j\)。

void kmp(){
    for(int i=1, j=0; i<=m; i++){
        while(j && s[i] != p[j + 1]){
            j = nxt[j];
        }

        if(s[i] == p[j + 1]){
            j++;
        }

        if(j == n){
            cout << i - n << ' ';
            j = nxt[j] + 1;
        }
    }
}

代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10, M = N * 10;

int n, m;
char p[N], s[M];
int nxt[N];

void init_nxt(){
    for(int i=2, j=0; i<=n; i++){
        while(j && p[i] != p[j + 1]){
            j = nxt[j];
        }
        
        if(p[i] == p[j + 1]){
            j++;
        }
        
        nxt[i] = j;
    }
}

void kmp(){
    for(int i=1, j=0; i<=m; i++){
        while(j && s[i] != p[j + 1]){
            j = nxt[j];
        }
        
        if(s[i] == p[j + 1]){
            j++;
        }
        
        if(j == n){
            cout << i - n + 1 << ' ';
            j = nxt[j];
        }
    }
}

int main()
{
    cin >> n >> p + 1 >> m >> s + 1;
    
    // 求 nxt[i] 过程
    init_nxt();
    
    // kmp 匹配过程
    kmp();
    
    return 0;
}

时间复杂度

时间复杂度 \(\Theta(n)\)