妙妙题!
简要题意:给定一个 \(n\),有一个 \(n\times n\) 的网格图。
有 \(4n\) 个方向 \(U/D/L/R_{1,2,\dots,n}\),如下图:

对于每个方向,有个限制:数 \(x\)。你可以进行 \(\le x\) 次推棋子,把一个棋子放到当前方向指向的第一格,然后如果原来第一格有棋子,把它放到第二格,如果原来第二格有棋子,把它放到第三格 \(\dots\)(就是类似推箱子的过程)
如果最终会推出棋盘,那么这次操作不能进行。
输入 \(U/D/L/R_{1,2,\dots,n}\) 表示 \(4n\) 个方向的操作数限制。
\(4n\) 个方向的 \(x\) 总和 \(\sum x=n^2\)。
请构造一个合法的推棋子方案(即按顺序输入方向),或报告无解(输出 \(\texttt{NO}\))。
可以参考原题样例理解。
考虑推棋子这件事对全局的影响太大,转换成把这颗棋子放到当前方向的第一格空位,这样就好做多了。
把每个格子向它上下左右 \(4\) 个方向连边(上下左右分别连向它),流量为 \(1\)。
把 \(S\) 向 \(4n\) 个方向连边,流量为这个方向的推次数限制。把 \(n\times n\) 个格子向 \(T\) 连流量为 \(1\) 的边。
跑网络流,发现合法方案一定是满流,即流量为 \(n^2\)。
同时我们也可以求出每个格子是由哪个方向放进去的(很显然,实在不会看代码)
发现这是比二分图匹配弱的(感性理解一下),参照二分图匹配来分析复杂度是 \(O(|E|\sqrt{|V|})=O(n^2\sqrt{n^2})=O(n^3)\)。
PS:这一步有不用网络流的做法,但我无法理解,于是放了网络流的做法,大家可以对照那个代码自行研究。
网络流部分代码(只放连边和判断方向,\(\texttt{dinic}\) 相信大家都会了):
scanf("%d",&n);S=0;T=n*n+4*n+1;
for(int i=1;i<=n;i++) scanf("%d",&U[i]),add(S,n*n+i,U[i]);
for(int i=1;i<=n;i++) scanf("%d",&D[i]),add(S,n*n+n+i,D[i]);
for(int i=1;i<=n;i++) scanf("%d",&L[i]),add(S,n*n+2*n+i,L[i]);
for(int i=1;i<=n;i++) scanf("%d",&R[i]),add(S,n*n+3*n+i,R[i]);
#define wz(i,j) (i-1)*n+j
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++)
add(n*n+2*n+i,wz(i,j),1),add(n*n+3*n+i,wz(i,j),1),add(n*n+j,wz(i,j),1),add(n*n+n+j,wz(i,j),1),add(wz(i,j),T,1);
//连边
while(bfs()) memcpy(_head,head,sizeof(head)),ans+=dfs(S,1e9);
if(ans!=n*n) return 0*puts("NO");
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++)
for(int k=head[wz(i,j)];k;k=e[k].nex)
{
int to=e[k].to;
if(to!=T&&e[k].w){a[i][j]=(to-n*n-1)/n;break;}
}//判断方向
这还没完,我们只求出了每个格子是由哪个方向放进去的,并不知道顺序,下面解决这个问题。
考虑如果放了一个某方向的棋子,则这个棋子沿这个方向之前一定都被填满了。
考虑 \(\texttt{dfs}\),对于某个格子,\(\texttt{for}\) 找到这个方向所有未被填的格子,然后 \(\texttt{dfs}\) 那个格子(如果没有就不执行),最后把这个格子填上。
伪代码:
void dfs(int x,int y)
{
for(枚举往前格子) if(!vis[nx][ny]) dfs(nx,ny);
vis[x][y]=1;cout<<方向<<"\n";
}
伪代码也不一定对,理解意思就行。
上面的方法如果每个格子只被 \(\texttt{dfs}\) 一次,那么总复杂度是 \(O(n^2\times n)=O(n^3)\)。
但是事实上并不一定在这样,会出现这种情况。
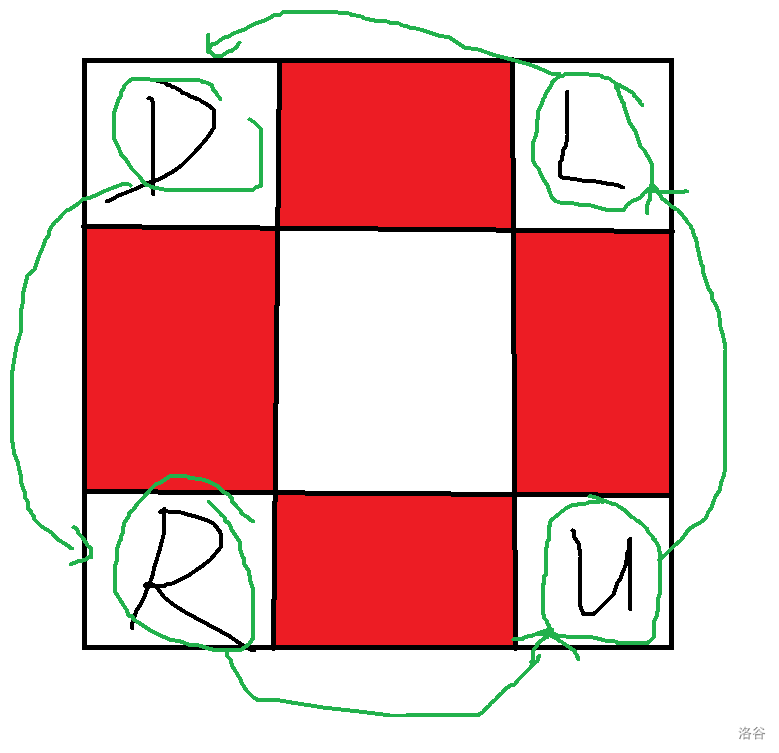
就相当于有环,这时候我们不好确定顺序,可以做如下变换:
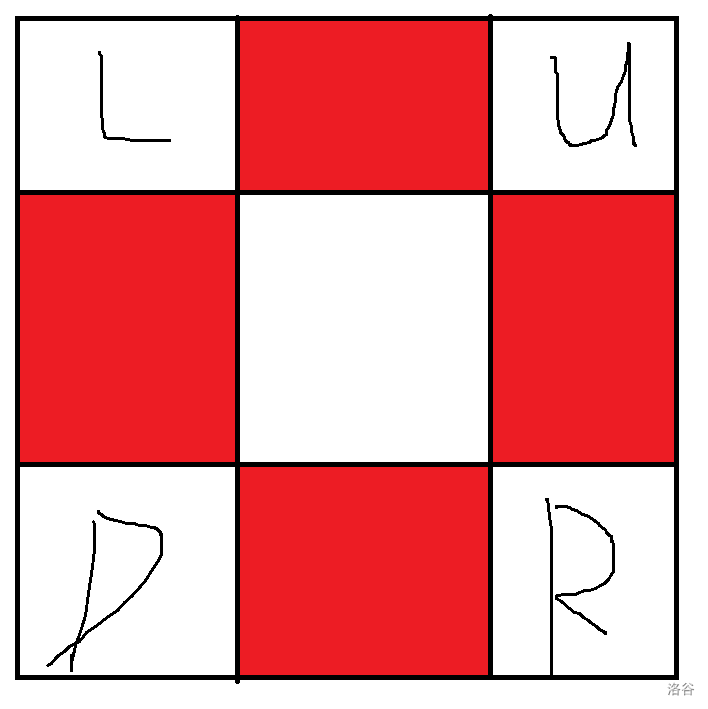
发现这样依然是符合要求的,而且消去了环。
说一下实现方法,记一个 \(v\) 表示一个点输出了没有,记一个 \(V\) 表示这个点遍历了一次(无环)还是两次(有环),感性理解一下。然后往前 \(\texttt{for}\) 再 \(\texttt{dfs}\) 找环,有一些细节可以看代码。
代码:
bool dfs1(int x,int y)
{
if(V[x][y]) return V[x][y]=0,1;V[x][y]=1;
int adx=dx[a[x][y]],ady=dy[a[x][y]],nx=x+adx,ny=y+ady,col=a[x][y];//有可能之后会更改颜色所以要先记颜色。
while(nx>0&&ny>0&&nx<=n&&ny<=n)
{
if(!v[nx][ny]&&dfs1(nx,ny))
{
a[nx][ny]=col;//如果循环更改不记颜色会寄
if(V[x][y]) return V[x][y]=0,1;
return dfs1(x,y);//注意如果更改了颜色就要重新 dfs
}
nx+=adx;ny+=ady;
}v[x][y]=1;//一定要最后才把这个变成1
return 0*printf("%c%d\n",c[a[x][y]],a[x][y]<2?y:x);
}
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) dfs1(i,j);//可能还有没做完的,要多次。
势能分析
这里先给出结论,这样做是 \(O(n^3)\) 的。
下面的势能分析可能跟别人讲的都不一样,可以参考着理解。
其实势能分析你可以理解为:选取一个恰当的状态,有值 \(d\)(看做势能),这个值每减少 \(x\) 就会增加 \(f(x)\) 的复杂度(可以理解为于势能转化为动能),那么总复杂度就是 \(\sum f(x)\)。对它估界,一般 \(f(x)=\operatorname{poly}(n)\times \operatorname{poly}\log(n)\),于是 \(\sum f(x)\le f(\sum x)=f(d)\)。
比如单调队栈每减少一个数就会增加 \(1\) 的复杂度,于是线性。线段树合并线段树每少 \(1\) 个节点复杂度就会 \(+1\) ,于是复杂度是节点数就是 \(O(n\log n)\)。
来看这题。定义势能 \(d\) 为原来 \(n^2\) 个格子到它自己边界(比如格子里写 \(L\) 就是左边界)的距离和,\(d\le n^3\)。举 \(L\to D\) 的例子来说,这次遍历对复杂度的影响是 \(pos_L-pos_D\) 的,同时 \(L\) 离自己边界的距离也减少了这个值。于是复杂度就是 \(d\),即 \(O(n^3)\) 的。
于是做完了,总复杂度 \(O(n^3)\) 的。
代码:
#include<bits/stdc++.h>
#define LL long long
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
const int N=305,M=N*N+4*N,dx[4]={-1,1,0,0},dy[4]={0,0,-1,1};
const char c[4]={'U','D','L','R'};
struct edge{int to,nex,w;}e[M*200];
int n,m,S,T,tot=1,head[M],_head[M],d[M],ans,U[N],D[N],L[N],R[N],a[N][N];
bool v[N][N],V[N][N];
inline void add(int u,int v,int w)
{
e[++tot]={v,head[u],w};head[u]=tot;
e[++tot]={u,head[v],0};head[v]=tot;
}
inline bool bfs()
{
memset(d,0,sizeof(d));d[S]=1;queue<int>q;q.push(S);
while(!q.empty())
{
int t=q.front();q.pop();
for(int i=head[t];i;i=e[i].nex)
{
int to=e[i].to;
if(!d[to]&&e[i].w>0) d[to]=d[t]+1,q.push(to);
}
}
return d[T];
}
int dfs(int x,int F)
{
if(x==T) return F;
int tt=F;
for(int &i=_head[x];i;i=e[i].nex)
{
int to=e[i].to;
if(d[to]==d[x]+1&&e[i].w>0)
{
int t=dfs(to,min(tt,e[i].w));
tt-=t;e[i].w-=t;e[i^1].w+=t;
if(!tt) break;
}
}
if(tt==F) d[x]=0;
return F-tt;
}
bool dfs1(int x,int y)
{
if(V[x][y]) return V[x][y]=0,1;V[x][y]=1;
int adx=dx[a[x][y]],ady=dy[a[x][y]],nx=x+adx,ny=y+ady,col=a[x][y];
while(nx>0&&ny>0&&nx<=n&&ny<=n)
{
if(!v[nx][ny]&&dfs1(nx,ny))
{
a[nx][ny]=col;
if(V[x][y]) return V[x][y]=0,1;
return dfs1(x,y);
}
nx+=adx;ny+=ady;
}v[x][y]=1;
return 0*printf("%c%d\n",c[a[x][y]],a[x][y]<2?y:x);
}
int main()
{
scanf("%d",&n);S=0;T=n*n+4*n+1;
for(int i=1;i<=n;i++) scanf("%d",&U[i]),add(S,n*n+i,U[i]);
for(int i=1;i<=n;i++) scanf("%d",&D[i]),add(S,n*n+n+i,D[i]);
for(int i=1;i<=n;i++) scanf("%d",&L[i]),add(S,n*n+2*n+i,L[i]);
for(int i=1;i<=n;i++) scanf("%d",&R[i]),add(S,n*n+3*n+i,R[i]);
#define wz(i,j) (i-1)*n+j
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++)
add(n*n+2*n+i,wz(i,j),1),add(n*n+3*n+i,wz(i,j),1),add(n*n+j,wz(i,j),1),add(n*n+n+j,wz(i,j),1),add(wz(i,j),T,1);
while(bfs()) memcpy(_head,head,sizeof(head)),ans+=dfs(S,1e9);
if(ans!=n*n) return 0*puts("NO");
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++)
for(int k=head[wz(i,j)];k;k=e[k].nex)
{
int to=e[k].to;
if(to!=T&&e[k].w){a[i][j]=(to-n*n-1)/n;break;}
}
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) dfs1(i,j);
return 0;
}
很困难,\(\texttt{tourist}\) 都没有场切(写了 \(n=40\) 的做法,\(2000\) 分,满分 \(2100\),所以只有 \(100\) 分给 \(n=300\)),听说写了个 \(O(n^5)\) 的做法,很强。
标签:head,格子,FESTIVAL,题解,复杂度,texttt,dfs,int,2016 From: https://www.cnblogs.com/HaHeHyt/p/17288966.html