首页 > 其他分享 >字符串（提高组）详解

字符串（提高组）详解

时间：2023-04-01 18:56:04浏览次数：46  
标签：int 提高 样例 leq 详解 字符串 mathcal border

字符串（提高组）详解

前提提要：本文为提高组字符串，不涉及到后缀科技等相关算法，请放心食用

Part 1. 字符串 Hash

题目概要

如题，给定 \(N\) 个字符串（第 \(i\) 个字符串长度为 \(M_i\)，字符串内包含数字、大小写字母，大小写敏感），请求出 \(N\) 个字符串中共有多少个不同的字符串。

输入格式

第一行包含一个整数 \(N\)，为字符串的个数。

接下来 \(N\) 行每行包含一个字符串，为所提供的字符串。

输出格式

输出包含一行，包含一个整数，为不同的字符串个数。

样例 #1

样例输入 #1

5
abc
aaaa
abc
abcc
12345

样例输出 #1

4

提示

对于 \(30\%\) 的数据：\(N\leq 10\)，\(M_i≈6\)，\(Mmax\leq 15\)。

对于 \(70\%\) 的数据：\(N\leq 1000\)，\(M_i≈100\)，\(Mmax\leq 150\)。

对于 \(100\%\) 的数据：\(N\leq 10000\)，\(M_i≈1000\)，\(Mmax\leq 1500\)。

样例说明：

样例中第一个字符串(abc)和第三个字符串(abc)是一样的，所以所提供字符串的集合为{aaaa,abc,abcc,12345}，故共计4个不同的字符串。

实现

我们来考虑一下，整数是怎么进行去重的？

很明显，给你一个整数 \(a\)，扔到一个数组下面，判断重复就行

那我们字符串呢？

能不能扔给一个字符串独有的标识符使得每个字符串不重？

有！！我们考虑吧字符串变成一个 \(BASE\) 进制下的整数，这个 \(BASE\) 取整数碰撞（也就是相同）的概率回小

我取的是 \(13331\)，你们取什么管不着，这样我们就可以得出一个数的哈希值

\[hash(S)=(\sum_{i}^{|S|} hash(S_{i-1})\cdot BASE + S_i-'a'+1)\mod Mod \]

注意几个点

  • \(Mod\) 建议取很大的整数，但是方便的话，我们可以使用 unsigned long long 的强大之处（自动溢出)
  • S[i]-'a'+1这里的+1不能省略，不然的话 \(a\) 和 \(ab\) 就没有区别了

简要代码

\(\mathcal{Code}\)

ull Hash(char s[]){
	int len=strlen(s);
	ull ans=0;
	for(int i=0;i<len;i++){
		ans=ans*base+(ull)s[i];//变成AS码
	}
	return ans;
}

区间 hash

如果我们要查询 \([l,r]\) 的hash值，怎么办呢？

我们可以类比十进制取考虑。

例如：我们这里有一个十进制数为：\(123456\)

我们要查询最后三位的哈希值，也就是 \([4,6]\) 的hash值（个人喜欢从一开始）

可以轻易口算得到：\(456=123456-123000\)，有了这个思路，我们可以写出代码

这里要预处理 \(P_i\) 为 \(BASE_i\)，注意初始化p[0]=1

\(\mathcal{Code}\)

P[0] = 1;
for (int i = 1; i <= n; i ++) 
    P[i] = P[i - 1] * BASE;

ull get(int l, int r) {return H[r] - H[l - 1] * P[r - l + 1]; }//自己推去

\(\mathcal{Practice}\) 1.

[P4391]([P4391 BOI2009]Radio Transmission 无线传输 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))

\(Practice\) 2.

[P5018]([P5018 NOIP2018 普及组] 对称二叉树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))

Part 2. KMP算法

【模板】KMP字符串匹配

题目描述

给出两个字符串 \(s_1\) 和 \(s_2\)，若 \(s_1\) 的区间 \([l, r]\) 子串与 \(s_2\) 完全相同，则称 \(s_2\) 在 \(s_1\) 中出现了，其出现位置为 \(l\)。
现在请你求出 \(s_2\) 在 \(s_1\) 中所有出现的位置。

定义一个字符串 \(s\) 的 border 为 \(s\) 的一个非 \(s\) 本身的子串 \(t\)，满足 \(t\) 既是 \(s\) 的前缀，又是 \(s\) 的后缀。
对于 \(s_2\)，你还需要求出对于其每个前缀 \(s'\) 的最长 border \(t'\) 的长度。

输入格式

第一行为一个字符串，即为 \(s_1\)。
第二行为一个字符串，即为 \(s_2\)。

输出格式

首先输出若干行，每行一个整数，按从小到大的顺序输出 \(s_2\) 在 \(s_1\) 中出现的位置。
最后一行输出 \(|s_2|\) 个整数，第 \(i\) 个整数表示 \(s_2\) 的长度为 \(i\) 的前缀的最长 border 长度。

样例 #1

样例输入 #1
ABABABC
ABA
样例输出 #1
1
3
0 0 1

提示

样例 1 解释

。

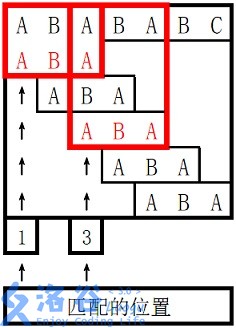对于 \(s_2\) 长度为 \(3\) 的前缀 ABA，字符串 A 既是其后缀也是其前缀，且是最长的，因此最长 border 长度为 \(1\)。

数据规模与约定

本题采用多测试点捆绑测试，共有 3 个子任务。

  • Subtask 1（30 points）：\(|s_1| \leq 15\)，\(|s_2| \leq 5\)。
  • Subtask 2（40 points）：\(|s_1| \leq 10^4\)，\(|s_2| \leq 10^2\)。
  • Subtask 3（30 points）：无特殊约定。

对于全部的测试点，保证 \(1 \leq |s_1|,|s_2| \leq 10^6\)，\(s_1, s_2\) 中均只含大写英文字母。

分析

这一部分非常难理解，建议用心食用

先了解前缀函数

概念：

  • \(border\)：形象的说就是左边突出去的部分和右边突进来的部分长度相等且相等

用数学符号表示就是：\(S[1…k]=S[n-k+1…n]\)，那么 \(S[1…k]\) 就是 \(S\) 的一个 \(border\)

  • 前缀数组：\(\pi [i]\) 表示 \(S[1…i]\) 之中最长 \(border\) 的长度

​ 例如上图就是 \(\pi _n=3\)

性质：

  • 记 \(A\) 为前缀 \(S[1…i]\) 的 \(border\) 长集合，\(A=\{a_1,a_2,…,a_n \}\)，也就是 \(S[1…i]\) 的所有 \(border\) 为 \(S[1…a_1],S[1…a_2],…,S[1…a_n]\)，为了方便，我们约定 \(a_1>a_2>…>a_n\)
  • 记 \(B\) 为前缀 \(S[1…i-1]\) 的 \(border\) 长集合，\(B=\{b_1,b_2,…,b_m \}\)，也就是 \(S[1…i-1]\) 的所有 \(border\) 为 \(S[1…b_1],S[1…b_2],…,S[1…b_m]\)，为了方便，我们约定 \(b_1>b_2>…>b_m\)

有如下两个结论

  • 如果 \(x \in A\) 那么必须有 \(x-1\in B\)

证明：

证明

其中，第二张图的蓝色 \(border\) 是另外一个，别管呀

  • \(\pi i\le \pi_{i-1}+1\)

​ 这个画图看看就行，只有证明复杂度的时候才会用

  • \(\pi a_1=a_2……\)

​ 这个可以画图理解，很重要！！！！记也要记下来

于是，我们就可以有个思路

我们求 \(\pi i\) 的时候可以枚举 \(i-1\) 的 \(border\)（用性质2)，来检查是否满足条件

当 \(i-1\) 没有 \(border\) 可以匹配的时候，\(\pi i\) 有可能等于0或1，特判之即可

代码惊人的简短

\(\mathcal{Code}\)

    scanf("%s", S + 1), n = strlen(S + 1);
    for(int i = 2;i <= n;++ i){
        int p = N[i - 1];
        while(S[p + 1] != S[i] && p != 0) p = N[p];//枚举i-1的border
        if(S[p + 1] == S[i]) N[i] = p + 1;//特判，这里是合并过得，可以展开
    }

那 \(KMP\) 就迎刃而解了

我们题目是 \(T\) 在 \(S\) 中出现多少次，我们可以把字符串变成：\(T+'.'+S\)

对这个字符串进行 \(border\) 即可（这只是理解)

\(\mathcal{Code}\)

#include <bits/stdc++.h>

using namespace std;

const int MAXN = 1e6 + 7;

char S[MAXN], T[MAXN];
int n, m, N[MAXN], M[MAXN];

int main () {
	cin >> S + 1 >> T + 1;
	n = strlen(S + 1), m = strlen(T + 1);
	
	N[1] = 0;
	for(int i = 2; i <= m; i ++) {
		int p = N[i - 1];
		while (T[p + 1] != T[i] && p != 0) p = N[p];
		if (T[p + 1] == T[i]) N[i] = p + 1;//1的
		else N[i] = 0; 
	}
	
	for (int i = 1/*注意*/; i <= n; i ++) {
		int p = M[i - 1];
		while (T[p + 1] != S[i] && p != 0) p = N[p];//注意
		if (T[p + 1] == S[i]) M[i] = p + 1;
		else M[i] = 0;
		if (M[i] == m) cout << i - m + 1 << endl;
	}
	for (int i = 1; i <= m; i ++) cout << N[i] << ' ';
	return 0;
}

时间复杂度为 \(\mathcal{O}(n+m)\)，证明偏复杂，感兴趣的可以去了解

扩展 ：失配树

由 \(\pi\) 数组，我们可以建一个树

图

由以下性质

  • 每个节点的祖先都是他的 \(border\)
  • 他的父亲是他的最长 \(border\)

于是我们可以在上面跑树上倍增什么的

\(\mathcal{Practice}\) 1.

[CF126B](Password - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))

这里浅浅提一下，因为 \((1,n)\) 之间长度越长的 \(border\) 越有可能和前面和后面造成 \(border\)，多了也不会死，所以我们把最长的 \(border\) 求出来和 \([1,n]\) 之间的 \(border\) 比较长度就行

\(\mathcal{Practice}\) 2.

[P3435]([P3435 POI2006] OKR-Periods of Words - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))

这里也提一下，因为要求最长周期，根据我们以前求周期那个图可以知道，要让他们的 \(border\) 最短转移到失配树上就是求离根节点最近的节点，这里可以类似动态规划的解法，\(\mathcal{O}(n)\) 求出答案

\(\mathcal{Practice}\) 3.

[P2375]([P2375 NOI2014] 动物园 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))

Part 3.字典树

字典树简而言之就是把字符串插到树上

重点在构建字典树（代码实现）

  • 定义一个字典树类（或命名空间）
const int MAXM = 26 + 26 + 10 + 7;
const int MAXL = 3e6 + 7;

namespace Trie{
	int size, C[MAXL][MAXM], S[MAXL];
}

其中，\(C_{i,x}\) 表示从 \(i\) 这个节点走 \(x\) 这条边到的节点的编号

\(size\) 是一个动态指针

\(S_i\) 表示 \(i\) 这个节点有多少个绿色框框

  • 因为大小写和数字都有，我们要映射一下
int to_int(char c) {
    if (isdigit(c)) return c - '0' + 1;
    if (islower(c)) return c - 'a' + 10 + 1;
    if (isupper(c)) return c - 'A' + 10 + 26 + 1;
}
  • 清空（多次不清空，清零两行泪
void clean() {
    for (int i = 0; i <= size; i ++) S[i] = 0;
    for (int i = 0; i <= size; i ++)
        for (int j = 1; j <= 26 + 26 + 10; j ++) 
            C[i][j] = 0;
    size = 0;
}
  • 插入
void insert(char X[]) {
    int p = 0; ++ S[0];//头结点
    for (int i = 0; X[i]; i ++) {
        int w = to_int(X[i]);
        if (C[p][w]) p = C[p][w];//如果有就走 
        else p = C[p][w] = ++ size;//没有就开辟
        ++ S[p]; //加上
    }
}
  • 查询
int query(char X[]) {
    int p = 0;
    for (int i = 0; X[i]; i ++) {
        int w = to_int(X[i]);
        if (C[p][w]) p = C[p][w]; 
        else p = C[p][w] = ++ size;
    }
    return S[p];//返回即可
}

\(\mathcal{Code}\)

#include <bits/stdc++.h>

using namespace std;

const int MAXN = 1e5 + 3;
const int MAXM = 26 + 26 + 10 + 7;
const int MAXL = 3e6 + 7;

namespace Trie{
	int size, C[MAXL][MAXM], S[MAXL];
	int to_int(char c) {
		if (isdigit(c)) return c - '0' + 1;
		if (islower(c)) return c - 'a' + 10 + 1;
		if (isupper(c)) return c - 'A' + 10 + 26 + 1;
	}
	
	void clean() {
		for (int i = 0; i <= size; i ++) S[i] = 0;
		for (int i = 0; i <= size; i ++)
			for (int j = 1; j <= 26 + 26 + 10; j ++) 
				C[i][j] = 0;
		size = 0;
	}
	
	void insert(char X[]) {
		int p = 0; ++ S[0];
		for (int i = 0; X[i]; i ++) {
			int w = to_int(X[i]);
			if (C[p][w]) p = C[p][w]; 
			else p = C[p][w] = ++ size;
			++ S[p]; 
		}
	}
	
	int query(char X[]) {
		int p = 0;
		for (int i = 0; X[i]; i ++) {
			int w = to_int(X[i]);
			if (C[p][w]) p = C[p][w]; 
			else p = C[p][w] = ++ size;
		}
		return S[p];
	}
} 

char A[MAXL];

int main () {
	int T;
	for (cin >> T; T; T --) {
		int n, q;
		cin >> n >> q;
		for (int i = 1; i <= n; i ++) {
			cin >> A;
			Trie :: insert(A);
		}
		for (int i = 1; i <= q; i ++) {
			cin >> A;
			cout << Trie :: query(A) << endl;
		}
		Trie :: clean();
	}
	return 0;
}

01字典树

简而言之，就是把整数变成二进制放进字典树里

俗话说：异或的题目先去考虑线性基和01Trie，再去考虑别的做法

可见01Trie的厉害之处

看道题

最长异或路径

题目描述

给定一棵 \(n\) 个点的带权树，结点下标从 \(1\) 开始到 \(n\)。寻找树中找两个结点，求最长的异或路径。

异或路径指的是指两个结点之间唯一路径上的所有边权的异或。

输入格式

第一行一个整数 \(n\)，表示点数。

接下来 \(n-1\) 行，给出 \(u,v,w\) ，分别表示树上的 \(u\) 点和 \(v\) 点有连边，边的权值是 \(w\)。

输出格式

一行，一个整数表示答案。

样例 #1

样例输入 #1
4
1 2 3
2 3 4
2 4 6
样例输出 #1
7

提示

最长异或序列是 \(1,2,3\)，答案是 \(7=3\oplus 4\)。

数据范围

\(1\le n \le 100000;0 < u,v \le n;0 \le w < 2^{31}\)。

分析

由于异或的自反性

\(i\) 到 \(j\) 的异或和可以看做 \(1\) 到 \(i\) 和 \(1\) 到 \(j\) 的异或和

记 \(a_i\) 为 \(1\) 到 \(i\) 的异或和

问题就转换成了，求

\[\max_{1\le i,j\le n} \{a_i \oplus a_j\} \]

我们枚举 \(i\)，看能不能找到一个 \(j\) 使得

\[\max_{1\le j\le n} \{a_p \oplus a_j\} \]

这样的话，显然01Trie是可以做到的

因为异或每一位不一样才会是1，所以我们每次走他的相反边即可（没有的就不走呗QWQ

于是就打出代码

注意以下几点

  • 从高位到低位建立
  • 看准值域定数组

\(\mathcal{Code}\)

#include <bits/stdc++.h>

using namespace std;

const int MAXN = 1e5 + 7;

namespace Trie01{
	const int SIZ = 3.1e6 + 7;
	int size, L[SIZ], R[SIZ];
	
	void insert(int x) {
		int p = 0;
		for (int i = 31; i >= 1; i --) {
			if (x & (1 << i - 1)) p = (R[p] ? R[p] : R[p] = ++ size);
			else p = (L[p] ? L[p] : L[p] = ++ size);
		}
	}
	
	int query(int x) {
		int p = 0, ret = 0;
		for (int i = 30; i >= 0; i --) {
			if (x & (1 << i)) {
				if (L[p]) p = L[p], ret |= 1 << i;
				else p = R[p];
			} else {
				if (R[p]) p = R[p], ret |= 1 << i;
				else p = L[p]; 
			}
		}
		return ret;
	}
}

struct node{
	int nxt, to, v;
}edge[2 * MAXN];
int H[MAXN], e_cnt;
inline void add(int from, int to, int v) {edge[++ e_cnt].to = to, edge[e_cnt].nxt = H[from], H[from] = e_cnt; edge[e_cnt].v = v; }

int X[MAXN];
void dfs(int u, int f) {
	for (int i = H[u]; i; i = edge[i].nxt) {
		if (edge[i].to != f)
			X[edge[i].to] = X[u] ^ edge[i].v, dfs(edge[i].to, u); 
	}
}

int n;

int main () {
	cin >> n;
	for (int i = 1, u, v, w; i < n; i ++) {
		cin >> u >> v >> w;
		add(u, v, w); add(v, u, w);
	}
	dfs(1, 0);
	int ans = 0;
	for (int i = 1; i <= n; i ++) {
		ans = max(ans, Trie01 :: query(X[i]));
		Trie01 :: insert(X[i]);
	}
	cout << ans << endl;
	return 0;
}

扩展

压缩01Trie树

后语

字符串是门高深的学问，要多加练习

标签：int,提高,样例,leq,详解,字符串,mathcal,border
From： https://www.cnblogs.com/Phrvth/p/17279108.html

相关文章

  • 【入门】Go语言排序算法详解
    1、冒泡排序冒泡排序是一种简单的排序算法，它重复地遍历要排序的列表，比较相邻的两个元素，并在必要时交换它们的位置，直到没有任何一对元素需要交换为止。该算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。packagemainimport"fmt"//我们定义了一个名为`bu......
  • Java protected 关键字详解
    很多介绍Java语言的书籍(包括《Java编程思想》)都对protected介绍的比较的简单，基本都是一句话，就是: 被protected修饰的成员对于本包和其子类可见。这种说法有点太过含糊，常常会对大家造成误解。实际上，protected的可见性在于两点：基类的protected成员是包内可见的，并且对子类......
  • stat函数详解
    stat函数详解作用：获取文件信息头文件：#include<sys/types.h>#include<sys/stat.h>#include<unistd.h>函数原型：**intstat(constcharpath,structstatbuf)返回值：成功返回0，失败返回-1；参数：文件路径（名），structstat类型的结构体structstat结构体详解：structstat{......
  • day11| 20.有效的括号；150.逆波兰表达式求值；1047.删除字符串中的所有相邻重复项
    20.有效的括号 题目简述：给定一个只包括'('，')'，'{'，'}'，'['，']' 的字符串s，判断字符串是否有效。有效字符串需满足：左括号必须用相同类型的右括号闭合。左括号必须以正确的顺序闭合。每个右括号都有一个对应的相同类型的左括号。 思路：1.利用一个栈实现2.构建一个字典，键......
  • 3·1HTTP协议特点、3·2详解URL与URI的区别与联系、3·3HTTP报文结构分析、3·4HTTP请
     HTTP协议特点支持客户/服务器模式客户/服务器模式工作的方式是由客户端向服务器发出请求,服务器端响应请求,并进行相应服务简单快速 客户端向服务器请求服务时，只需传输请求方法和路径 请求方法常用的有GET、HEAD、POST。每种方法规......
  • HTTP协议特点&详解UR与URL的区别与联系
    HTTP协议特点支持客户/服务器模式客户/服务器模式工作的方式是由客户端向服务器发送请求，服务器端响应请求，并进行相应服务   简单快速客户向服务器请求服务时，只需传送请求方法和路径请求方法常用的有GET，HEAD，POST。每种方法规定了客户与服务器练习的......
  • Spring（Bean详解）
    GoF之工厂模式GoF是指二十三种设计模式GoF23种设计模式可分为三大类：创建型（5个）：解决对象创建问题。单例模式工厂方法模式抽象工厂模式建造者模式原型模式结构型（7个）：一些类或对象组合在一起的经典结构。代理模式装饰模式适配器模式组......
  • HJ66 配置文件恢复_字典_字符串
    思路：1、把命令和执行对录入一字串字典和二字串字典2、取字典的可以与输入对比3、为了保证唯一性，用c常数增加1来判断是否唯一。4、最后根据c值统一打印输出1importsys2a=[]3forlineinsys.stdin:4a.append(line.strip().split())5#print(a)6d1={"rese......
  • 字符串、列表、元组、集合
    一、字符串1、定义使用引号（单引号、双引号、三引号）引起来的内容，就是字符串。2、例子#1、单引号str1='abc'#2、双引号str2="abc"#3、三引号str3='''abc'''#4、定义字符串，#字符串本身包含单引号，定义的时候不能使用单引号。字符串本身包含双引号......
  • 阶段小结：批量删除的时候使用 this.id的详解、jquery里面的$(this)和this的区别、面试
    this.id指的是当前对象的id比如我点击了button那么此button按钮的id就可以用this.id文章目录this.id指的是当前对象的id比如我点击了button那么此button按钮的id就可以用this.id我们先看项目里面方式1：利用样式，可以隐藏，但是不推荐方式二主角this.id方式：给点击删除的时候......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99