首页 > 其他分享 >重链剖分学习笔记+做题记录

重链剖分学习笔记+做题记录

时间：2023-03-20 16:57:13浏览次数：47  
标签：fv 剖分 int ed dfn 做题 ans 重链 fu

一、理论知识

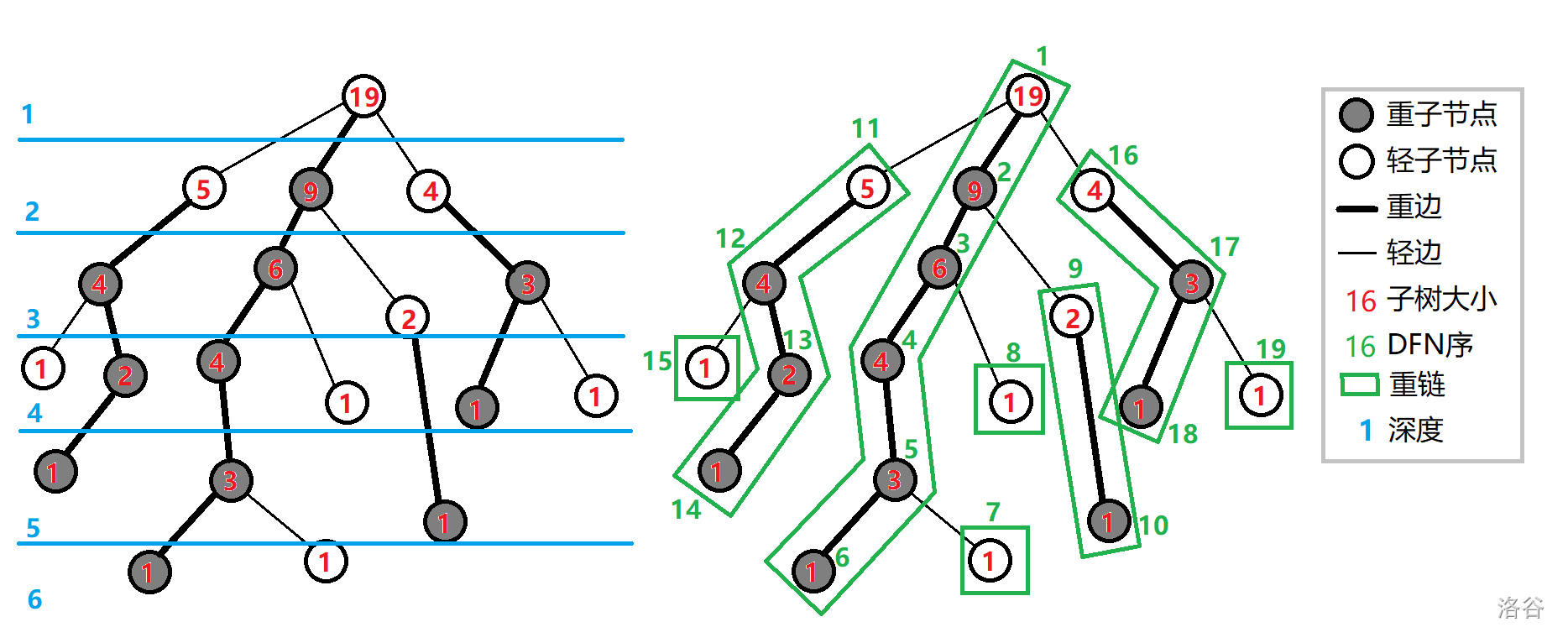
首先放一张图（明显是 OI-Wiki 的）：

  • \(u\) 的子节点 \(p_1,p_2,\dots,p_k\) 中子树最大的节点叫做重儿子，如有多个，任取其一，记作 \(son_u\)。

  • \(u\) 除掉 \(son_u\) 以外的子节点叫做轻儿子。

  • 重儿子与其父节点连的边叫做重边。

  • 不是重边的边叫做轻边。

  • 若干重边组成的极长的链叫做重链。（单个轻儿子节点单独形成一条重链）

这样，\(n\) 个节点的树被分为 \(\log n\) 条重链。

我们可以在重链上开线段树，维护路径 & 子树的修改 & 查询问题。

这样单次复杂度就是 \(O(\log^2 n)\) 的。

二、两次 dfs

  • \(son(u)\) 表示 \(u\) 的重儿子，若 \(u\) 为叶子节点则 \(son(u)=-1\)。

  • \(siz(u)\) 表示以 \(u\) 为根的子树大小。

  • \(depth(u)\) 表示 \(u\) 的深度。

  • \(fa(u)\) 表示 \(u\) 的父亲。

  • \(top(u)\) 表示 \(u\) 所在重链的链头。

  • \(dfn(u)\) 表示 \(u\) 的 DFS 序。

  • \(rk(u)\) 表示 \(dfn(v)\) 为 \(u\) 的 \(v\)，即 \(dfn(rk(u))=u\)。

int son[N], siz[N], depth[N], fa[N], top[N], dfn[N], rk[N];
inline void dfs1 (int u) {
	son[u] = -1;
	siz[u] = 1;
	for (int i = head[u]; i ; i = ed[i].nxt) {
		if (!depth[ed[i].to]) {
			depth[ed[i].to] = depth[u] + 1;
			fa[ed[i].to] = u;
			dfs1 (ed[i].to);
			siz[u] += siz[ed[i].to];
			if (son[u] == -1 || siz[ed[i].to] > siz[son[u]]) son[u] = ed[i].to; 
		}
	}
}
int tmd, mod;
inline void dfs2 (int u, int ck) {
	top[u] = ck;
	tmd ++;
	dfn[u] = tmd;
	rk[tmd] = u;
	if (son[u] == -1) return ;
	dfs2 (son[u], ck);
	for (int i = head[u]; i ; i = ed[i].nxt) {
		if (ed[i].to != son[u] && ed[i].to != fa[u]) dfs2 (ed[i].to, ed[i].to);
	}
}

三、路径上操作

按照重链一个一个向上跳，在重链上修改，非常模板化：

inline void upd_path (int u, int v, int d) {
	int fu = top[u], fv = top[v];
	while (fu != fv) {
		if (depth[fu] >= depth[fv]) {
			sg.update (1, 1, n, dfn[fu], dfn[u], d);
			u = fa[fu]; 
		}
		else {
			sg.update (1, 1, n, dfn[fv], dfn[v], d);
			v = fa[fv]; 
		}
		fu = top[u];
		fv = top[v];
	}
	if (dfn[u] < dfn[v]) sg.update (1, 1, n, dfn[u], dfn[v], d);
	else sg.update (1, 1, n, dfn[v], dfn[u], d);
	return ;
}

查询操作只需要改一改即可，以洛谷 P3384 为例：

inline int query (int u, int v) {
	int ans = 0, fu = top[u], fv = top[v];
	while (fu != fv) {
		if (depth[fu] >= depth[fv]) {
			ans = (ans + sg.query (1, 1, n, dfn[fu], dfn[u])) % mod;
			u = fa[fu];
		}
		else {
			ans = (ans + sg.query (1, 1, n, dfn[fv], dfn[v])) % mod;
			v = fa[fv]; 
		}
		fu = top[u];
		fv = top[v];
	}
	if (dfn[u] < dfn[v]) ans = (ans + sg.query (1, 1, n, dfn[u], dfn[v])) % mod;
	else ans = (ans + sg.query (1, 1, n, dfn[v], dfn[u])) % mod;
	return ans;
}

四、子树上操作

我们发现以 \(u\) 为根的子树的所有的节点的 DFS 序构在 \([dfn(u),dfn(u)+siz(u)-1]\) 之内。

inline void upd_subtree (int u, int d) {
	int L = dfn[u], R = dfn[u] + siz[u] - 1;
	sg.update (1, 1, n, L, R, d);
}
inline int query_subtree (int u) {
	int L = dfn[u], R = dfn[u] + siz[u] - 1;
	return sg.query (1, 1, n, L, R);
}

五、例题

P2590 树的统计

板子题，线段树改改就过。

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/hash_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#ifdef LOCAL
#include "algo/debug.h"
#else
#define debug(...) 42
#endif
typedef long long ll;
typedef pair < int, int > PII;
typedef int itn;
mt19937 RND_MAKER (chrono :: steady_clock :: now ().time_since_epoch ().count ());
inline ll randomly (const ll l, const ll r) {return (RND_MAKER () ^ (1ull << 63)) % (r - l + 1) + l;}
#define int long long
const double pi = acos (-1);
//__gnu_pbds :: tree < Key, Mapped, Cmp_Fn = std :: less < Key >, Tag = rb_tree_tag, Node_Upadte = null_tree_node_update, Allocator = std :: allocator < char > > ;
//__gnu_pbds :: tree < PPS, __gnu_pbds :: null_type, less < PPS >, __gnu_pbds :: rb_tree_tag, __gnu_pbds :: tree_order_statistics_node_update > tr;
const int N = 3e4 + 5;
int head[N], n, val[N], qwq[N];
struct edge {
	int to, nxt;
} ed[N << 1];
int cnt;
inline void add_edge (int u, int v) {
	cnt ++;
	ed[cnt].to = v;
	ed[cnt].nxt = head[u];
	head[u] = cnt;
}
int son[N], siz[N], depth[N], fa[N], top[N], dfn[N], rk[N];
inline void dfs1 (int u) {
	son[u] = -1;
	siz[u] = 1;
	for (int i = head[u]; i ; i = ed[i].nxt) {
		if (!depth[ed[i].to]) {
			depth[ed[i].to] = depth[u] + 1;
			fa[ed[i].to] = u;
			dfs1 (ed[i].to);
			siz[u] += siz[ed[i].to];
			if (son[u] == -1 || siz[ed[i].to] > siz[son[u]]) son[u] = ed[i].to; 
		}
	}
}
int tmd;
inline void dfs2 (int u, int ck) {
	top[u] = ck;
	tmd ++;
	dfn[u] = tmd;
	rk[tmd] = u;
	if (son[u] == -1) return ;
	dfs2 (son[u], ck);
	for (int i = head[u]; i ; i = ed[i].nxt) {
		if (ed[i].to != son[u] && ed[i].to != fa[u]) dfs2 (ed[i].to, ed[i].to);
	}
}
struct segment_tree {
	int sum[N << 2], mx[N << 2], inc[N << 2];
	inline void push_up (int u) {
		sum[u] = sum[u << 1] + sum[u << 1 | 1];
		mx[u] = max (mx[u << 1], mx[u << 1 | 1]);
	}
	inline void push_down (int u, int l, int r) {
		if (inc[u] == -2e18) return ;
		inc[u << 1] = inc[u << 1 | 1] = inc[u];
		mx[u << 1] = mx[u << 1 | 1] = inc[u];
		int mid = l + r >> 1;
		sum[u << 1] = (mid - l + 1) * inc[u];
		sum[u << 1 | 1] = (r - mid) * inc[u];
		inc[u] = -2e18;
	}
	inline void build (int u, int l, int r) {
		inc[u] = -2e18;
		if (l == r) {
			sum[u] = mx[u] = qwq[l];
			return ; 
		}
		int mid = l + r >> 1;
		build (u << 1, l, mid);
		build (u << 1 | 1, mid + 1, r);
		push_up (u);
	}
	inline void update (int u, int l, int r, int x, int y, int v) {
		if (x <= l && r <= y) {
			sum[u] = (r - l + 1) * v;
			mx[u] = v;
			inc[u] = v;
			return ;
		}
		push_down (u, l, r);
		int mid = l + r >> 1;
		if (x <= mid) update (u << 1, l, mid, x, y, v);
		if (y > mid) update (u << 1 | 1, mid + 1, r, x, y, v);
		push_up (u);
	}
	inline int query_sum (int u, int l, int r, int x, int y) {
		if (x <= l && r <= y) return sum[u];
		push_down (u, l, r);
		int mid = l + r >> 1, ans = 0;
		if (x <= mid) ans += query_sum (u << 1, l, mid, x, y);
		if (y > mid) ans += query_sum (u << 1 | 1, mid + 1, r, x, y);
		return ans;
	}
	inline int query_max (int u, int l, int r, int x, int y) {
		if (x <= l && r <= y) return mx[u];
		push_down (u, l, r);
		int mid = l + r >> 1, ans = -2e18;
		if (x <= mid) ans = max (ans, query_max (u << 1, l, mid, x, y));
		if (y > mid) ans = max (ans, query_max (u << 1 | 1, mid + 1, r, x, y));
		return ans;
	}
} sg;
inline void update (int u, int w) {
	sg.update (1, 1, n, dfn[u], dfn[u], w);
}
inline int query_max (int u, int v) {
	int ans = -2e18, fu = top[u], fv = top[v];
	while (fu != fv) {
		if (depth[fu] >= depth[fv]) {
			ans = max (ans, sg.query_max (1, 1, n, dfn[fu], dfn[u]));
			u = fa[fu];
		}
		else {
			ans = max (ans, sg.query_max (1, 1, n, dfn[fv], dfn[v]));
			v = fa[fv]; 
		}
		fu = top[u];
		fv = top[v];
	}
	if (dfn[u] < dfn[v]) ans = max (ans, sg.query_max (1, 1, n, dfn[u], dfn[v]));
	else ans = max (ans, sg.query_max (1, 1, n, dfn[v], dfn[u]));
	return ans;
}
inline int query_sum (int u, int v) {
	int ans = 0, fu = top[u], fv = top[v];
	while (fu != fv) {
		if (depth[fu] >= depth[fv]) {
			ans += sg.query_sum (1, 1, n, dfn[fu], dfn[u]);
			u = fa[fu];
		}
		else {
			ans += sg.query_sum (1, 1, n, dfn[fv], dfn[v]);
			v = fa[fv]; 
		}
		fu = top[u];
		fv = top[v];
	}
	if (dfn[u] < dfn[v]) ans += sg.query_sum (1, 1, n, dfn[u], dfn[v]);
	else ans += sg.query_sum (1, 1, n, dfn[v], dfn[u]);
	return ans;
}
signed main () {
	scanf ("%lld", &n);
	for (int i = 1;i < n; ++ i) {
		int u, v;
		scanf ("%lld %lld", &u, &v);
		add_edge (u, v);
		add_edge (v, u);
	}
	depth[1] = 1;
	dfs1 (1);
	dfs2 (1, 1);
	for (int i = 1;i <= n; ++ i) scanf ("%lld", &val[i]);
	for (int i = 1;i <= n; ++ i) qwq[dfn[i]] = val[i];
	sg.build (1, 1, n);
	int q;
	scanf ("%lld", &q);
	while (q --) {
		char op[10];
		scanf ("%s", op + 1);
		if (op[1] == 'C') {
			int x, y;
			scanf ("%lld %lld", &x, &y);
			update (x, y);
		}
		else if (op[2] == 'M') {
			int s, t;
			scanf ("%lld %lld", &s, &t);
			printf ("%lld\n", query_max (s, t));
		}
		else {
			int s, t;
			scanf ("%lld %lld", &s, &t);
			printf ("%lld\n", query_sum (s, t));
		}
	}
	return 0;
}

P3379 【模板】最近公共祖先（LCA）

模拟跳重链，直到跳到 LCA 就停止，连线段树都不用。

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/hash_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#ifdef LOCAL
#include "algo/debug.h"
#else
#define debug(...) 42
#endif
typedef long long ll;
typedef pair < int, int > PII;
typedef int itn;
mt19937 RND_MAKER (chrono :: steady_clock :: now ().time_since_epoch ().count ());
inline ll randomly (const ll l, const ll r) {return (RND_MAKER () ^ (1ull << 63)) % (r - l + 1) + l;}
//#define int long long
const double pi = acos (-1);
//__gnu_pbds :: tree < Key, Mapped, Cmp_Fn = std :: less < Key >, Tag = rb_tree_tag, Node_Upadte = null_tree_node_update, Allocator = std :: allocator < char > > ;
//__gnu_pbds :: tree < PPS, __gnu_pbds :: null_type, less < PPS >, __gnu_pbds :: rb_tree_tag, __gnu_pbds :: tree_order_statistics_node_update > tr;
const int N = 5e5 + 5;
int head[N], n, val[N], qwq[N];
struct edge {
	int to, nxt;
} ed[N << 1];
int cnt;
inline void add_edge (int u, int v) {
	cnt ++;
	ed[cnt].to = v;
	ed[cnt].nxt = head[u];
	head[u] = cnt;
}
int son[N], siz[N], depth[N], fa[N], top[N], dfn[N], rk[N];
inline void dfs1 (int u) {
	son[u] = -1;
	siz[u] = 1;
	for (int i = head[u]; i ; i = ed[i].nxt) {
		if (!depth[ed[i].to]) {
			depth[ed[i].to] = depth[u] + 1;
			fa[ed[i].to] = u;
			dfs1 (ed[i].to);
			siz[u] += siz[ed[i].to];
			if (son[u] == -1 || siz[ed[i].to] > siz[son[u]]) son[u] = ed[i].to;
		}
	}
}
int tmd;
inline void dfs2 (int u, int ck) {
	top[u] = ck;
	tmd ++;
	dfn[u] = tmd;
	rk[tmd] = u;
	if (son[u] == -1) return ;
	dfs2 (son[u], ck);
	for (int i = head[u]; i ; i = ed[i].nxt) {
		if (ed[i].to != son[u] && ed[i].to != fa[u]) dfs2 (ed[i].to, ed[i].to);
	}
}
inline int LCA (int u, int v) {
	while (top[u] != top[v]) {
		if (depth[top[u]] < depth[top[v]]) v = fa[top[v]];
		else u = fa[top[u]];
	}
	if (depth[u] < depth[v]) return u;
	else return v;
}
signed main () {
	int m, s;
	scanf ("%d %d %d", &n, &m, &s);
	for (int i = 1;i < n; ++ i) {
		int u, v;
		scanf ("%d %d", &u, &v);
		add_edge (u, v);
		add_edge (v, u);
	}
	depth[s] = 1;
	dfs1 (s);
	dfs2 (s, s);
	while (m --) {
		int u, v;
		scanf ("%d %d", &u, &v);
		printf ("%d\n", LCA (u, v));
	}
	return 0;
}

P3258 [JLOI2014]松鼠的新家

相当于在 \([a_1 \to a_2),[a_2 \to a_3),\dots,[a_{n-1} \to a_n)\) 上都放一块糖果。

最后输出每个节点的糖果数量。

可以用树链剖分解决，线段树维护一下糖果数量。

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/hash_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#ifdef LOCAL
#include "algo/debug.h"
#else
#define debug(...) 42
#endif
typedef long long ll;
typedef pair < int, int > PII;
typedef int itn;
mt19937 RND_MAKER (chrono :: steady_clock :: now ().time_since_epoch ().count ());
inline ll randomly (const ll l, const ll r) {return (RND_MAKER () ^ (1ull << 63)) % (r - l + 1) + l;}
#define int long long
const double pi = acos (-1);
//__gnu_pbds :: tree < Key, Mapped, Cmp_Fn = std :: less < Key >, Tag = rb_tree_tag, Node_Upadte = null_tree_node_update, Allocator = std :: allocator < char > > ;
//__gnu_pbds :: tree < PPS, __gnu_pbds :: null_type, less < PPS >, __gnu_pbds :: rb_tree_tag, __gnu_pbds :: tree_order_statistics_node_update > tr;
const int N = 3e5 + 5;
int head[N], n, val[N], qwq[N];
struct edge {
	int to, nxt;
} ed[N << 1];
int cnt;
inline void add_edge (int u, int v) {
	cnt ++;
	ed[cnt].to = v;
	ed[cnt].nxt = head[u];
	head[u] = cnt;
}
int son[N], siz[N], depth[N], fa[N], top[N], dfn[N], rk[N];
inline void dfs1 (int u) {
	son[u] = -1;
	siz[u] = 1;
	for (int i = head[u]; i ; i = ed[i].nxt) {
		if (!depth[ed[i].to]) {
			depth[ed[i].to] = depth[u] + 1;
			fa[ed[i].to] = u;
			dfs1 (ed[i].to);
			siz[u] += siz[ed[i].to];
			if (son[u] == -1 || siz[ed[i].to] > siz[son[u]]) son[u] = ed[i].to; 
		}
	}
}
int tmd;
inline void dfs2 (int u, int ck) {
	top[u] = ck;
	tmd ++;
	dfn[u] = tmd;
	rk[tmd] = u;
	if (son[u] == -1) return ;
	dfs2 (son[u], ck);
	for (int i = head[u]; i ; i = ed[i].nxt) {
		if (ed[i].to != son[u] && ed[i].to != fa[u]) dfs2 (ed[i].to, ed[i].to);
	}
}
struct segment_tree {
	int sum[N << 2], inc[N << 2];
	inline void push_up (int u) {
		sum[u] = (sum[u << 1] + sum[u << 1 | 1]);
	}
	inline void push_down (int u, int l, int r) {
		if (inc[u] == 0) return ;
		int mid = l + r >> 1;
		inc[u << 1] = (inc[u << 1] + inc[u]);
		inc[u << 1 | 1] = (inc[u << 1 | 1] + inc[u]);
		sum[u << 1] = (sum[u << 1] + (mid - l + 1) * inc[u]);
		sum[u << 1 | 1] = (sum[u << 1 | 1] + (r - mid) * inc[u]);
		inc[u] = 0;
	}
	inline void build (int u, int l, int r) {
		if (l == r) {
			sum[u] = qwq[l];
			return ;
		}
		int mid = l + r >> 1;
		build (u << 1, l, mid);
		build (u << 1 | 1, mid + 1, r);
		push_up (u);
	}
	inline void update (int u, int l, int r, int x, int y, int v) {
		if (x <= l && r <= y) {
			sum[u] = (sum[u] + (r - l + 1) * v);
			inc[u] = (inc[u] + v);
			return ; 
		}
		push_down (u, l, r);
		int mid = l + r >> 1;
		if (x <= mid) update (u << 1, l, mid, x, y, v);
		if (y > mid) update (u << 1 | 1, mid + 1, r, x, y, v);
		push_up (u);
	}
	inline int query (int u, int l, int r, int x, int y) {
		if (x <= l && r <= y) return sum[u];
		push_down (u, l, r);
		int mid = l + r >> 1, ans = 0;
		if (x <= mid) ans = (ans + query (u << 1, l, mid, x, y));
		if (y > mid) ans = (ans + query (u << 1 | 1, mid + 1, r, x, y));
		return ans;
	}
} sg;
inline int query (int u, int v) {
	int ans = 0, fu = top[u], fv = top[v];
	while (fu != fv) {
		if (depth[fu] >= depth[fv]) {
			ans = (ans + sg.query (1, 1, n, dfn[fu], dfn[u]));
			u = fa[fu];
		}
		else {
			ans = (ans + sg.query (1, 1, n, dfn[fv], dfn[v]));
			v = fa[fv]; 
		}
		fu = top[u];
		fv = top[v];
	}
	if (dfn[u] < dfn[v]) ans = (ans + sg.query (1, 1, n, dfn[u], dfn[v]));
	else ans = (ans + sg.query (1, 1, n, dfn[v], dfn[u]));
	return ans;
}
inline void upd_path (int u, int v, int d) {
	int fu = top[u], fv = top[v];
	while (fu != fv) {
		if (depth[fu] >= depth[fv]) {
			sg.update (1, 1, n, dfn[fu], dfn[u], d);
			u = fa[fu]; 
		}
		else {
			sg.update (1, 1, n, dfn[fv], dfn[v], d);
			v = fa[fv]; 
		}
		fu = top[u];
		fv = top[v];
	}
	if (dfn[u] < dfn[v]) sg.update (1, 1, n, dfn[u], dfn[v], d);
	else sg.update (1, 1, n, dfn[v], dfn[u], d);
	return ;
}
signed main () {
	scanf ("%lld", &n);
	for (int i = 1;i <= n; ++ i) scanf ("%lld", &val[i]);
	for (int i = 1;i < n; ++ i) {
		int u, v;
		scanf ("%lld %lld", &u, &v);
		add_edge (u, v);
		add_edge (v, u);
	}
	depth[1] = 1;
	dfs1 (1);
	dfs2 (1, 1);
	for (int i = 1;i <= n; ++ i) qwq[dfn[i]] = 0;
	sg.build (1, 1, n);
	for (int i = 1;i < n; ++ i) {
		upd_path (val[i], val[i + 1], 1);
		upd_path (val[i + 1], val[i + 1], -1);
	}
	for (int i = 1;i <= n; ++ i) printf ("%lld\n", query (i, i));
	return 0;
}

P3178 [HAOI2015]树上操作

裸题一道，话不多说：

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/hash_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#ifdef LOCAL
#include "algo/debug.h"
#else
#define debug(...) 42
#endif
typedef long long ll;
typedef pair < int, int > PII;
typedef int itn;
mt19937 RND_MAKER (chrono :: steady_clock :: now ().time_since_epoch ().count ());
inline ll randomly (const ll l, const ll r) {return (RND_MAKER () ^ (1ull << 63)) % (r - l + 1) + l;}
#define int long long
const double pi = acos (-1);
//__gnu_pbds :: tree < Key, Mapped, Cmp_Fn = std :: less < Key >, Tag = rb_tree_tag, Node_Upadte = null_tree_node_update, Allocator = std :: allocator < char > > ;
//__gnu_pbds :: tree < PPS, __gnu_pbds :: null_type, less < PPS >, __gnu_pbds :: rb_tree_tag, __gnu_pbds :: tree_order_statistics_node_update > tr;
const int N = 3e5 + 5;
int head[N], n, val[N], qwq[N];
struct edge {
	int to, nxt;
} ed[N << 1];
int cnt;
inline void add_edge (int u, int v) {
	cnt ++;
	ed[cnt].to = v;
	ed[cnt].nxt = head[u];
	head[u] = cnt;
}
int son[N], siz[N], depth[N], fa[N], top[N], dfn[N], rk[N];
inline void dfs1 (int u) {
	son[u] = -1;
	siz[u] = 1;
	for (int i = head[u]; i ; i = ed[i].nxt) {
		if (!depth[ed[i].to]) {
			depth[ed[i].to] = depth[u] + 1;
			fa[ed[i].to] = u;
			dfs1 (ed[i].to);
			siz[u] += siz[ed[i].to];
			if (son[u] == -1 || siz[ed[i].to] > siz[son[u]]) son[u] = ed[i].to; 
		}
	}
}
int tmd;
inline void dfs2 (int u, int ck) {
	top[u] = ck;
	tmd ++;
	dfn[u] = tmd;
	rk[tmd] = u;
	if (son[u] == -1) return ;
	dfs2 (son[u], ck);
	for (int i = head[u]; i ; i = ed[i].nxt) {
		if (ed[i].to != son[u] && ed[i].to != fa[u]) dfs2 (ed[i].to, ed[i].to);
	}
}
struct segment_tree {
	int sum[N << 2], inc[N << 2];
	inline void push_up (int u) {
		sum[u] = (sum[u << 1] + sum[u << 1 | 1]);
	}
	inline void push_down (int u, int l, int r) {
		if (inc[u] == 0) return ;
		int mid = l + r >> 1;
		inc[u << 1] = (inc[u << 1] + inc[u]);
		inc[u << 1 | 1] = (inc[u << 1 | 1] + inc[u]);
		sum[u << 1] = (sum[u << 1] + (mid - l + 1) * inc[u]);
		sum[u << 1 | 1] = (sum[u << 1 | 1] + (r - mid) * inc[u]);
		inc[u] = 0;
	}
	inline void build (int u, int l, int r) {
		if (l == r) {
			sum[u] = qwq[l];
			return ;
		}
		int mid = l + r >> 1;
		build (u << 1, l, mid);
		build (u << 1 | 1, mid + 1, r);
		push_up (u);
	}
	inline void update (int u, int l, int r, int x, int y, int v) {
		if (x <= l && r <= y) {
			sum[u] = (sum[u] + (r - l + 1) * v);
			inc[u] = (inc[u] + v);
			return ; 
		}
		push_down (u, l, r);
		int mid = l + r >> 1;
		if (x <= mid) update (u << 1, l, mid, x, y, v);
		if (y > mid) update (u << 1 | 1, mid + 1, r, x, y, v);
		push_up (u);
	}
	inline int query (int u, int l, int r, int x, int y) {
		if (x <= l && r <= y) return sum[u];
		push_down (u, l, r);
		int mid = l + r >> 1, ans = 0;
		if (x <= mid) ans = (ans + query (u << 1, l, mid, x, y));
		if (y > mid) ans = (ans + query (u << 1 | 1, mid + 1, r, x, y));
		return ans;
	}
} sg;
inline int query (int u, int v) {
	int ans = 0, fu = top[u], fv = top[v];
	while (fu != fv) {
		if (depth[fu] >= depth[fv]) {
			ans = (ans + sg.query (1, 1, n, dfn[fu], dfn[u]));
			u = fa[fu];
		}
		else {
			ans = (ans + sg.query (1, 1, n, dfn[fv], dfn[v]));
			v = fa[fv]; 
		}
		fu = top[u];
		fv = top[v];
	}
	if (dfn[u] < dfn[v]) ans = (ans + sg.query (1, 1, n, dfn[u], dfn[v]));
	else ans = (ans + sg.query (1, 1, n, dfn[v], dfn[u]));
	return ans;
}
inline void upd_path (int u, int v, int d) {
	int fu = top[u], fv = top[v];
	while (fu != fv) {
		if (depth[fu] >= depth[fv]) {
			sg.update (1, 1, n, dfn[fu], dfn[u], d);
			u = fa[fu]; 
		}
		else {
			sg.update (1, 1, n, dfn[fv], dfn[v], d);
			v = fa[fv]; 
		}
		fu = top[u];
		fv = top[v];
	}
	if (dfn[u] < dfn[v]) sg.update (1, 1, n, dfn[u], dfn[v], d);
	else sg.update (1, 1, n, dfn[v], dfn[u], d);
	return ;
}
inline void upd_subtree (int u, int d) {
	int L = dfn[u], R = dfn[u] + siz[u] - 1;
	sg.update (1, 1, n, L, R, d); 
}
signed main () {
	int m;
	scanf ("%lld %lld", &n, &m);
	for (int i = 1;i <= n; ++ i) scanf ("%lld", &val[i]);
	for (int i = 1;i < n; ++ i) {
		int u, v;
		scanf ("%lld %lld", &u, &v);
		add_edge (u, v);
		add_edge (v, u);
	}
	depth[1] = 1;
	dfs1 (1);
	dfs2 (1, 1);
	for (int i = 1;i <= n; ++ i) qwq[dfn[i]] = val[i];
	sg.build (1, 1, n);
	while (m --) {
		int op;
		scanf ("%lld", &op);
		if (op == 1) {
			int u, d;
			scanf ("%lld %lld", &u, &d);
			upd_path (u, u, d);
		}
		else if (op == 2) {
			int u, d;
			scanf ("%lld %lld", &u, &d);
			upd_subtree (u, d);			
		}
		else {
			int u;
			scanf ("%lld", &u);
			printf ("%lld\n", query (1, u)); 
		}
	}
	return 0;
}

P2146 [NOI2015] 软件包管理器

  • install x 查询 \(0\) 到 \(x\) 有多少 uninstall 状态的节点，并将 \(0\) 到 \(x\) 上的所有节点都设为 install 状态。

  • uninstall x 查询 \(x\) 的子树内有多少 install 状态的节点，并将 \(x\) 的子树内的所有节点都设为 uninstall 状态。

这个可以用区间赋值的线段树+树链剖分维护。

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/hash_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#ifdef LOCAL
#include "algo/debug.h"
#else
#define debug(...) 42
#endif
typedef long long ll;
typedef pair < int, int > PII;
typedef int itn;
mt19937 RND_MAKER (chrono :: steady_clock :: now ().time_since_epoch ().count ());
inline ll randomly (const ll l, const ll r) {return (RND_MAKER () ^ (1ull << 63)) % (r - l + 1) + l;}
#define int long long
const double pi = acos (-1);
//__gnu_pbds :: tree < Key, Mapped, Cmp_Fn = std :: less < Key >, Tag = rb_tree_tag, Node_Upadte = null_tree_node_update, Allocator = std :: allocator < char > > ;
//__gnu_pbds :: tree < PPS, __gnu_pbds :: null_type, less < PPS >, __gnu_pbds :: rb_tree_tag, __gnu_pbds :: tree_order_statistics_node_update > tr;
const int N = 1e5 + 5;
int head[N], n, val[N], qwq[N];
struct edge {
	int to, nxt;
} ed[N << 1];
int cnt;
inline void add_edge (int u, int v) {
	cnt ++;
	ed[cnt].to = v;
	ed[cnt].nxt = head[u];
	head[u] = cnt;
}
int son[N], siz[N], depth[N], fa[N], top[N], dfn[N], rk[N];
inline void dfs1 (int u) {
	son[u] = -1;
	siz[u] = 1;
	for (int i = head[u]; i ; i = ed[i].nxt) {
		if (!depth[ed[i].to]) {
			depth[ed[i].to] = depth[u] + 1;
			fa[ed[i].to] = u;
			dfs1 (ed[i].to);
			siz[u] += siz[ed[i].to];
			if (son[u] == -1 || siz[ed[i].to] > siz[son[u]]) son[u] = ed[i].to; 
		}
	}
}
int tmd;
inline void dfs2 (int u, int ck) {
	top[u] = ck;
	tmd ++;
	dfn[u] = tmd;
	rk[tmd] = u;
	if (son[u] == -1) return ;
	dfs2 (son[u], ck);
	for (int i = head[u]; i ; i = ed[i].nxt) {
		if (ed[i].to != son[u] && ed[i].to != fa[u]) dfs2 (ed[i].to, ed[i].to);
	}
}
struct segment_tree {
	int sum[N << 2], inc[N << 2];
	inline void push_up (int u) {
		sum[u] = sum[u << 1] + sum[u << 1 | 1];
	}
	inline void push_down (int u, int l, int r) {
		if (inc[u] == -1) return ;
		inc[u << 1] = inc[u << 1 | 1] = inc[u];
		int mid = l + r >> 1;
		sum[u << 1] = (mid - l + 1) * inc[u];
		sum[u << 1 | 1] = (r - mid) * inc[u];
		inc[u] = -1; 
	}
	inline void build (int u, int l, int r) {
		inc[u] = -1; 
		if (l == r) {
			sum[u] = qwq[l];
			return ;
		}
		int mid = l + r >> 1;
		build (u << 1, l, mid);
		build (u << 1 | 1, mid + 1, r);
		push_up (u);
	}
	inline void update (int u, int l, int r, int x, int y, int v) {
		if (x <= l && r <= y) {
			sum[u] = (r - l + 1) * v;
			inc[u] = v;
			return ;
		}
		push_down (u, l, r);
		int mid = l + r >> 1;
		if (x <= mid) update (u << 1, l, mid, x, y, v);
		if (y > mid) update (u << 1 | 1, mid + 1, r, x, y, v);
		push_up (u);
	}
	inline int query (int u, int l, int r, int x, int y) {
		if (x <= l && r <= y) return sum[u];
		push_down (u, l, r);
		int mid = l + r >> 1, ans = 0;
		if (x <= mid) ans += query (u << 1, l, mid, x, y);
		if (y > mid) ans += query (u << 1 | 1, mid + 1, r, x, y);
		return ans; 
	}
} sg;
inline int query (int u, int v) {
	int ans = 0, fu = top[u], fv = top[v];
	while (fu != fv) {
		if (depth[fu] >= depth[fv]) {
			ans = (ans + sg.query (1, 1, n, dfn[fu], dfn[u]));
			u = fa[fu];
		}
		else {
			ans = (ans + sg.query (1, 1, n, dfn[fv], dfn[v]));
			v = fa[fv]; 
		}
		fu = top[u];
		fv = top[v];
	}
	if (dfn[u] < dfn[v]) ans = (ans + sg.query (1, 1, n, dfn[u], dfn[v]));
	else ans = (ans + sg.query (1, 1, n, dfn[v], dfn[u]));
	return ans;
}
inline void upd_path (int u, int v, int d) {
	int fu = top[u], fv = top[v];
	while (fu != fv) {
		if (depth[fu] >= depth[fv]) {
			sg.update (1, 1, n, dfn[fu], dfn[u], d);
			u = fa[fu]; 
		}
		else {
			sg.update (1, 1, n, dfn[fv], dfn[v], d);
			v = fa[fv]; 
		}
		fu = top[u];
		fv = top[v];
	}
	if (dfn[u] < dfn[v]) sg.update (1, 1, n, dfn[u], dfn[v], d);
	else sg.update (1, 1, n, dfn[v], dfn[u], d);
	return ;
}
inline void upd_subtree (int u, int d) {
	int L = dfn[u], R = dfn[u] + siz[u] - 1;
	sg.update (1, 1, n, L, R, d); 
}
inline int query_subtree (int u) {
	int L = dfn[u], R = dfn[u] + siz[u] - 1;
	return sg.query (1, 1, n, L, R); 
}
signed main () {
	int m;
	scanf ("%lld", &n);
	for (int i = 2;i <= n; ++ i) {
		int u;
		scanf ("%lld", &u);
		u ++;
		add_edge (i, u);
		add_edge (u, i);
	} 
	depth[1] = 1;
	dfs1 (1);
	dfs2 (1, 1);
	for (int i = 1;i <= n; ++ i) qwq[dfn[i]] = 0;
	sg.build (1, 1, n);
	scanf ("%lld", &m);
	while (m --) {
		char opt[20];
		scanf ("%s", opt + 1);
		if (opt[1] == 'i') {
			int u;
			scanf ("%lld", &u);
			u ++;
			int qwqq = depth[u] - query (1, u);
			printf ("%lld\n", qwqq);
			upd_path (1, u, 1);
		}
		else {
			int u;
			scanf ("%lld", &u);
			u ++;
			int qwqq = query_subtree (u);
			printf ("%lld\n", qwqq);
			upd_subtree (u, 0);			
		}
	}
	return 0;
}

标签：fv,剖分,int,ed,dfn,做题,ans,重链,fu
From： https://www.cnblogs.com/transitivity-ptqwq/p/17236887.html

相关文章

  • 树链剖分 学习笔记
    apple365:这个东西没有不可替代的作用重链剖分按照重儿子和轻儿子划分。第一遍dfs求出siz[],fa[],dep[],son[]。第二遍打dfn。每次走重儿子会走出一条重链。之后......
  • 03. 广义表多重链表
    一、广义表  广义表是线性表的推广。对于线性表而言，n个元素都是基本的氮元素。在广义表中，这些元素不仅可以是单元素也可以是另一个广义表。structGNode{intTa......
  • python有序字典在做题中的使用.
    66.两个链表的第一个公共结点  题目  提交记录  讨论  题解  视频讲解输入两个链表，找出它们的第一个公共结点。当不存在公共节点时，返回空......
  • 【洛谷】P5904 [POI2014]HOT-Hotels（长链剖分）
    原题链接题意给出一棵有\(n\)个点的树，求有多少组点\((i,j,k)\)满足\(i,j,k\)两两之间的距离都相等。\((i,j,k)\)与\((i,k,j)\)算作同一组。\(1\len\le10^5\)......
  • 一些做题记录
    难度从\(1\sim10\)分类，越小越简单。CF1100D算法难度：2实现难度：3思维难度：7具体思路：这个数据范围很奇怪，而且，这东西很人类智慧。具体而言，先把王挪到棋盘正中间，然后将......
  • 2023/3/17 做题技巧总结
    T1对于一道题目，如果描述有类似于“对于\(\forallx,y\in\mathbb{S}\)都有\(x\oplusy\in\mathbb{S}\)（其中\(\oplus\)为任意满足交换律的运算）”的描述时，我......
  • 【CF1009F Dominant Indices】（长链剖分）
    原题链接题意给定一棵以\(1\)为根，\(n\)个节点的树。设\(d(u,x)\)为\(u\)子树中到\(u\)距离为\(x\)的节点数。对于每个点，求一个最小的\(k\)，使得\(d(u,k)\)......
  • pwn做题技巧
    Canary对抗canary策略1，泄露canary值2，泄露fs:28H内的值3，覆写fs:28H副本值4，劫持stack_chk_fail5，stacksmashing6，逐字节爆破（BROPgadget，相对限制多）GOT（globaloffsett......
  • P4387 洛谷做题笔记 2023313
    P4387洛谷做题笔记2023/3/13这道题的关键点在于，在入栈的同时可以完成出栈操作，这就需要在每一次压入时检测是否出栈。这道题还有一个易错点，就是在每一次询问之后，还必须......
  • 长链剖分优化
    概述长链剖分通过对DP状态的复用，有效地降低某些状态具备显著继承性的treedp（多为与当前子树深度有关的dp状态）的转移复杂度。也可以说这是把本质不同的dp状态......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99